四面体有限单元网格优化技术探讨

一般地，网格优化主要有两个途径（Lori，Carl，1997）：①光顺（Smoothing），即不改变拓扑结构，调整结点的位置；②连接变换（Reconnection），即改变网格的拓扑结构，调整结点间的连接，以质量较高的单元替换旧单元。这两种方法各有优势，只有综合使用才会有较好的效果。通常需将整个优化过程分为若干轮，在每轮中交替使用这两种方法。

一个有效的四面体单元形状参数对于等边四面体应取最大值1，对于形状极差、体积接近于零的四面体应取最小值0。常用的四面体形状参数有最小立体角θ、内外径比ρ和参数γ（Lo，1997）。

已知四面体T（P 1 P 2 P 3 P 4），定义l ij为连接顶点P i、P j的边长，V为四面体的体积，则最小立体角可表示为

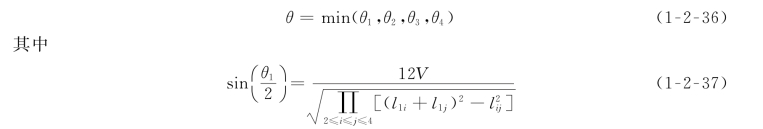
按式（1-2-37）依次轮换得到θ2、θ3、θ4。

内外径比ρ定义为

式中：r、R分别为四面体内切球和外接球的半径。

参数γ定义为

这三种参数有密切的联系，实际应用中可以取任意一种，并将其记为Q。

一、四面体单元的拓扑优化

此类优化主要包括边交换（Edge Swapping）和面交换（Face Swapping）（Lori，Carl，1997）。

1.边交换

边交换将共一条边的若干四面体改变拓扑结构（公共边和结点间的重新连接），以提高网格质量。m个四面体，经过边交换将变换为2m-4个四面体。随着m的增大，通过边交换提高网格质量的可能性急剧下降，在实际应用中，m≥7的情况已非常少见。

图1-2-18表示了以TB（TB垂直于纸面）为公共边的5个四面体（01BT）、（12BT）、（23BT）、（34BT）、（40BT）的一种可能的边变换形式：（012T）、（021B）、（024T）、（042B）、（234T）、（234B）。可以认为，这种边变换形式被等效△012、△024、△234唯一确定，显然这种T56的变换形式不止一种。

图1-2-18　边变换T56

边变换的关键问题是如何在若干种可能的变换形式中选择一种质量最好的变换形式。对于每一种形式的边变换i，可找出变换后新单元中质量最差的一个单元，并将其质量参数作为该变换形式的参数Qi。若某个边变换有m种变换形式，则最后所选用的第k种变换形式应满足

通常对于每一种变换形式产生的所有新单元都进行质量参数检验，以得出Qi，最后通过比较Qi（i=1，2，…，m）找出k。若将每一种变换形式产生的新单元的数目记为n，则需要进行m×n次单元质量参数检验。但实际上这m×n个单元中有很多是重复的，因而可能将需计算质量参数的单元数目大大减少，具体实现方式可参见Lori和Carl的论文（1997）。

2.面交换

面交换相对简单一些，图1-2-19表示一种常用的T23面交换，这实际是边交换T32的逆交换，这里不再详述。

二、四面体单元的非线性优化

1.非线性优化的引入(www.xing528.com)

传统的网格光顺方法主要是Laplacian光顺。对于网格中任一自由结点a，有n个相邻的四面体单元，这些四面体形成了一个以a为内部结点的多面体K，Laplacian光顺调整a至K的中心。

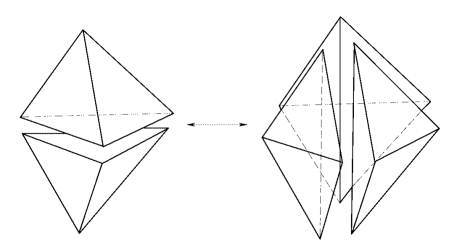
图1-2-19　面变换T23（边变换T32的逆交换）

式中：V为K的体积；X i、Y i、Zi为K的顶点坐标。

Laplacian光顺在平面网格优化中普遍使用，但该法在三维情况下常常失效。究其原因主要有：①没有证据表明多面体K的算术中心点就是最优点；②这是一种局部的改进方法，每次改进只涉及多面体K，只对一个结点a的位置进行调整。为克服上述缺点，有些研究者开始利用非线性最优化方法对三维网格质量进行改进。通过求一个在n维优化空间的网格质量目标函数的极值，得到可行域中真正的最优点，避免了Laplacian光顺的盲目性。理论上该优化空间可包括所有网格单元的结点，在每一步优化中，所有单元的结点可同时改变。优化空间的扩大，有利于获得更好的搜索方向，得到更有利的单元形状改变模式。

2.优化目标函数的定义

对网格进行全局优化，需要一个整体网格质量函数Qtol。Qtol通常有两种：可微型与不可微型。

设某网格有m个单元，可微型Qtol可取为这m个单元形状参数Q i的某种平均，例如

不可微型Qtol则可取为

由于在有限单元计算中，一个质量极差的单元的存在可能使整个求解失败，因此式（1-2-42）的平均化处理往往不能充分反映有限单元计算对网格质量的要求，故笔者采用式（1-2-43）作为网格质量函数，定义优化目标函数为

3.优化空间的确定

理论上优化空间可包括网格中所有单元的结点，但这样会使非线性优化求解规模过大。在实际应用中，Zavattieri等人（1996）引入了可动点、不可动点、当前可动点的概念来确定优化空间。

三维网格中所有边界点均为不可动点。当网格中质量最差的单元被优化后，其所属结点亦变为不可动点，从而得以继续优化网格中形状较差的其他单元。设在当前优化步中，形状最差的单元为T（P 1 P 2 P 3 P 4），若这4点中至少有1点为可动点，则定义这4点为“0层点”。与“0层点”中至少1点相连接的点定义为“1层点”，依次类推。取“M层点”中所有的可动点为当前可动点，则优化空间记为

式中：{X}为当前可动点的坐标向量。

若M取得足够大，则优化空间可包括整个网格的可动点。

4.非光滑目标函数的优化

通过对目标函数和优化空间的定义，网格优化问题转化为对式（1-2-44）求极大值的问题。式（1-2-44）中Qi为定义在R n的连续函数。这是一种非光滑优化问题，Zavattieri等人（1996）将Polak（1987）提出的最速下降算法应用于这种网格优化问题。

5.优化网格有效性的检验

对式（1-2-44）进行优化是一个无约束优化的纯数学问题，但实际上可动点位置的改变有一定的限制。可动点位置的改变不应改变网格原有的拓扑结构，否则会导致无效的网格。但将这种约束引入优化过程是一个很困难的问题，笔者采用的方法是对改变后的网格进行有效性检验，若满足有效性检验，则进入下一步光顺；若不满足，则调整步长，直至形成有效的网格。

利用本章介绍的方法，编制了程序GENCORE。