高效的三维四面体网格生成系统

1988年，Lohner等人开始将行波法拓展到三维区域的网格生成（Lohner，Parikh，1988）。我国采用该法（将该法称为推进网阵的方法）实现了三维区域中四面体网格的自动生成（李锡夔，方玉玲，1994）。针对不连续岩体，笔者也进行了三维复杂区域的四面体单元网格行波法研究（曹新红，陈尚法，陈胜宏，1998；陈尚法，陈胜宏，1998；Chen，Chen，Cao，2000；Xia，Chen，2001）。

一、一般性考虑

（一）基本原理

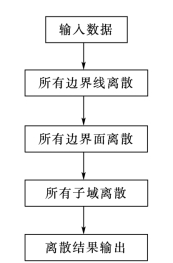
图1-2-11　四面体有限单元网格生成行波法的主程序流程

将包围子域的所有边界面离散，形成包围子域的三角形网格；将该网格上的三角形作为子域离散的初始生成波；每次在生成波上选择一个三角形，寻找一个点，与之构成一个四面体；从生成波上去掉此三角形。重复上述步骤，直到生成波上不再有三角形为止。图1-2-11表示了行波法生成四面体网格的主程序流程。

（二）边界种类

（1）边界面。包括空间平面、柱面、由若干个离散点定义的空间任意曲面。

（2）边界线。包括直线、弧线、对应于空间任意曲面的空间曲线。

（三）数据结构及组织

1.数据结构

三维区域的数据结构比二维区域要复杂得多，笔者采用5级数据结构来描述区域，如图1-2-12所示。第1级为研究区域，由若干个子域组成；第2级为子域，每个子域由若干个边界面包围而成；第3级为边界面，每个边界面由若干条边界线封闭而成；第4级为边界线，每条边界线由若干个点定义；第5级为点，每个点由其坐标定义。

2.数据组织

第1级数据说明组成研究区域的子域编号，记为d 1、d 2、…、d j、…；第2级数据说明子域d j的材料组号、开挖或回填编号、包围该子域的边界面个数、包围该子域的边界面编号，记为s1、s2、…、si、…；第3级数据说明边界面si的类型、参考点、定义该边界面的边界线条数、定义该边界面的边界线编号，记为l 1、l 2、…、l k、…；第4级数据说明边界线l k的类型、定义该边界线的点数、定义该边界线的点编号，记为P 1、P 2、…、P m、…；第5级数据说明点P m的编号及坐标，记为X m、Y m、Zm。

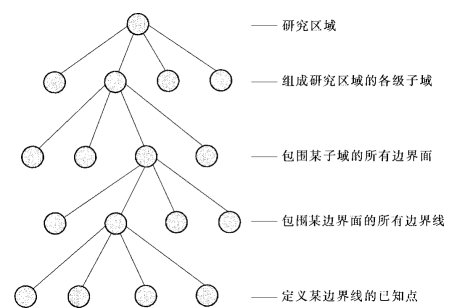
图1-2-12　描述区域的数据结构

3.数据组织方法

（1）组成研究区域的子域可以任意编号，与其位置无关。

（2）在整个区域内对所有边界面进行整体编号，其中包围子域d j的若干边界面的排列次序可以任意。对于相交的边界面，将其在每一个子域的部分视为不同的边界面。

（3）在整个区域内对所有边界线进行整体编号，其中包围边界面Si的若干条边界线应按逆时针方向排列，以使沿边界线前进的左手方向指向边界面的内部。也就是定义该边界面的正法线方向为该面所包围的子域的内部。

（4）在整个区域内对所有已知点进行编号。定义一条直线边界线的点为两个，一个为起点，一个为终点。对应于任意曲面的边界线，可以给出任意个定义该边界线的点。

（5）对于子域与子域的公交面，在给出子域的边界面编号时，以正负号来标志其正法线方向。在图1-2-13中，边界面Ⅰ对于区域1，编号为Ⅰ；而对于区域2，编号为-Ⅰ。

同理，对于边界线也以正负号来标志其前进方向。在图1-2-14中，边界线1和4的方向与逆时针走向一致，于是在边界面Ⅰ中，其编号分别为1和4；而边界线2和3的方向与逆时针走向相反，于是在边界面Ⅰ中，其编号分别为-2和-3。所以对于边界面Ⅰ，边界线定义为1、-2、-3、4。

图1-2-13　边界面正负向规定

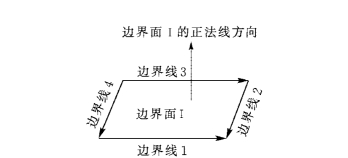
图1-2-14　边界线正负向规定

二、复杂域的处理

复杂域不仅指区域的边界复杂，而且该区域可能有孔洞，也可能有断层、软弱夹层、节理等结构面，并包含了不同的介质。此外，伴随结构物的施工与运行过程，还需动态变化网格。

依据“分而治之”的原则，设想将复杂区域分割成若干个由单一介质构成的子域，各个子域分别生成网格，再将各子域的网格“缝合”在一起，即可构成复杂区域的网格。于是在复杂区域上形成网格的问题就转化为将复杂区域分割成由单一介质构成的子域、在单一介质的子域上形成网格和各子域网格的“缝合”等三个相对较为简单的问题。

1.多连通域问题

生成二维区域网格时，一般采用加辅助线的方法，将多连通域转化成单连通域（图1-2-15）。

图1-2-15　加辅助线法(www.xing528.com)

（a）多连通域；（b）单连通域

生成三维区域网格时，若按类似的方法处理，则必须加辅助面，但在三维区域中加辅助面，涉及边界面求交问题，比较复杂。笔者在软件设计中，对多连通域问题，无论是边界面的离散还是子域的离散，都未采用加辅助面的方法，而是在数据结构设计时，给予如下特殊考虑：

（1）在边界面离散时，将所有边界线离散所得的数据放在同一个初始生成波上，生成波上的数据为所有待生成三角形的边和所有结点的坐标，而且在边界面离散的整个过程中，均对同一个生成波操作。

（2）在子域离散时，将所有边界面离散所得的数据放在同一个生成波上，生成波上的数据为所有待生成四面体单元的三角形和所有点的坐标，而且在子域的离散过程中，均对同一个生成波操作。

只要生成波的元素的正法线方向都指向未离散区域，不管是单连通域还是多连通域，使用同一个生成波都能够顺利生成网格。

2.动态网格问题

为满足结构施工过程中的动态网格要求，笔者把每期施工中开挖或填筑的子域作为单独的子域，对这些子域内单元和结点的形成施加特殊要求。例如，采用逆序法时，其单元号和结点号依次从最后开始排列。

3.结构面处理

节理、软弱夹层、断层等结构面在岩体中普遍存在。在有限单元法中，一般可将结构面剖分为节理单元，然后进行有限单元计算。对于厚度特别大的断层，也可以作为另外一种分区材料，划分为实体单元。下面着重介绍如何将结构面剖分为节理单元的问题。

（1）节理单元的形式。作为子域的边界面，结构面需剖分成三角形网格，以进行子域四面体网格离散。为了保证结构面网格与实体子域网格的协调性，可把结构面剖分为三棱柱单元（图1-2-16）。

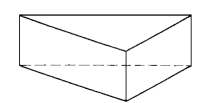
图1-2-16　三棱柱单元

（2）三棱柱单元的形成。在进行研究区域的描述时，需要定义结构面的上、下面，且需给出结构面的厚度t。在进行边界面的离散时，可选择结构面的上面（或下面）作为基准面进行离散，另一面的离散只需根据基准面的离散结果进行复制即可。最后依次连接结构面上、下面相对应的点，即可形成三棱柱单元（图1-2-16）。

（3）结构面相交的处理。两条结构面相交的现象很常见。在处理结构面相交时，笔者采用了一种简单的方法：在结构面相交处把结构面分成4个简单的单一结构面，然后按单一结构面的办法来处理，避免了综合考虑而不断修正的复杂性，也进一步体现了“分而治之”的优越性。

（4）弯曲结构面的处理。弯曲结构面上面（或下面）的点不在同一个平面上，故弯曲结构面的处理要比平面结构面更为复杂。笔者采用了以下步骤：①选择结构面的上面（或下面）作为基准面，并对基准面进行离散；②求基准面上各离散点的法线方向；③各离散点沿法线方向根据结构面的厚度复制相应点，全部离散点复制完毕后，即形成结构面的复制面的三角形网格；④对复制面与边界面相交处的点进行修正；⑤依次连接基准面和复制面上各对应的点，形成三棱柱单元。

三、主要算法

四面体单元的行波法生成已在很多文献中进行过讨论，下面给出主要算法步骤（图1-2-17）：

（1）在生成波上选择一个面ΔABC作为活动面。

（2）求出ΔABC的形心E的坐标，并由背景网格插值计算E点的网格尺度h。

（3）计算D点的坐标，D点位于ΔABC过E的法线上，且|AD|≈|BD|≈|CD|≈h。

（4）形成点集N 1、N 2、N P和面集F 1。

1）N 1中的点P满足以下条件：①P位于生成波上，且在ΔABC的正法线侧；②P位于以D为球心、1.25h为半径的球域内。

2）N 2是N 1的子集，N 2中的点P满足以下条件：①P位于以D为球心、h为半径的球域内；②A、B、C除外。

3）面集F 1是与N 1中的结点相连接的三角形面集，这些三角形也必须在生成波上，ΔABC除外。

4）形成新点集N P，N P中的点是D与ΔABC之间可能与ΔABC构成四面体的点。

（5）从N 1、N P中选择结点，与ΔABC构成一个四面体。

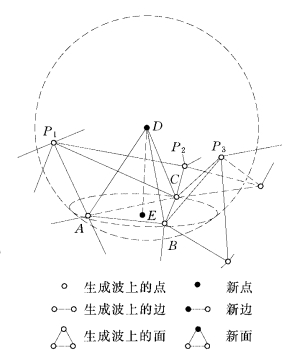
图1-2-17　三维行波法中的四面体单元生成

（6）检查该四面体是否通过有效性检查，即依次检查F 1中的面与新生成的四面体是否相交。

（7）检查该四面体是否通过辅助性检查。辅助性检查分两部分：①新生成四面体点、线、面与邻近四面体点、线、面的距离不应小于某一值D 1；②新生成四面体诸线、面之间角度不应小于某一值D 2。

（8）若步骤（7）的两项检查都通过，则执行步骤（9）。否则，若还有点可供选择，则返回执行步骤（5）；若无其他点可供选择，则返回执行步骤（1）。

（9）修正生成波上的数据结构，形成新的生成波。若生成波上面集不空，则返回执行步骤（1）；若面集已空，则子域离散完成。

一个有效的四面体生成算法应解决几何搜索和几何相交两个问题。Bonet等人通过对树型结构结点的访问，实现了很有效的几何搜索算法，在Bonet等人的文献中，还可找到几何相交算法的细节（Lohner，1988；Bonet，Peraire，1991；Peraire，Peiro，1992）。