一、数据结构
二维域数据组织的要点是把域、边、点三种几何元素按不同层次建立关系。用图1-2-6所示的浅埋地下洞室可以说明这种关系。
该计算域由6个子域组成,其中,子域①与其他子域分开的原因是存在岩层分界线;子域②~⑤的岩性相同,但由于结构面F1和F2切割,因此也必须分区处理;子域⑥则是洞室的开挖部分。每个子域都由一些曲线段组成,直线仅是其特例,以子域①为例,它以线段1、10、15、2为边界。线段是比域低一层次的几何元素,若为直线,则由其两端点唯一确定;若为曲线,则需3个以上的点来定义。图1-2-6中,线段15是直线,由点4和3确定;而线段19是1/2圆弧,由点9、16和8确定。点是最基本的几何元素,由坐标完全确定。在这种数据结构下,很容易指定某一区域的材料号与特定的材料参数对应,也很容易指定某一区域的开挖或填筑施工时间,而且可以较方便地描述边界条件。

图1-2-6 地下洞室及其几何元素
二、平面三角形网格的生成方法
平面三角形网格的生成问题已经被成功解决(Jin,Wiberg,1990),它是曲面三角形网格生成的基础,其基本计算步骤为(图1-2-7):
(1)由边界线离散结果得到初始生成波[1-2-7(a)]。
(2)每次生成新单元时,都选择生成波上长度最短的边AB作为活动边(Active Side)[图1-2-7(c)]。
(3)计算AB的中点D的坐标,并由单元尺度场插值计算D点的相邻单元尺寸h。单元尺度场的计算将在本篇第六章和第七章介绍。
(4)计算C点的坐标,C点满足以下条件:①C点位于AB内侧;②|AC|≈|BC|≈h。
(5)构造点集N 1,N 1中的点P满足以下条件:①P位于生成波上,且在AB内侧;②P位于以C点为圆心、h为半径的圆域内。
在图1-2-7(c)中,N 1包含P 1和P 2两个点。
(6)构造点集N 1的子集N 2,N 2中的点P满足以下条件:①ΔABP中不包含点集N 1中的结点(P点除外);②线段PD与生成波上任一边不相交(AB除外);③PA<nh,PB<nh,一般取n=1.5。
(7)若N 2非空,则选取N 2中相对于AB的张角(∠ABP)最大的点作为待生成点,构造ΔABP,修正生成波上的数据结构,返回步骤(2)。
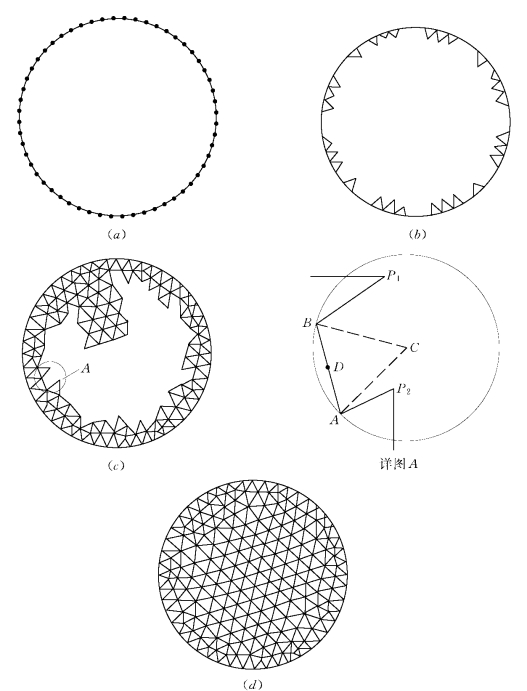
图1-2-7 平面三角形网格行波法生成过程
在图1-2-7(c)中,P 2点最终被选取。
(8)若N 2是空集,且C点满足以下条件:①ΔABC中不包含点集N 1中的点,②线段CD与生成波上任一边不相交(AB除外),则选取C点作为生成点,构造ΔABC,并修正生成波上的数据结构,返回步骤(2)。
(9)若C点不满足步骤(8)中的条件,则三角形生成失败,选取下一条边作为活动边,重复以上步骤。
(10)若生成波上边数为零,则该面离散全部完成[图1-2-7(d)]。
三、平面四边形网格的生成方法
平面四边形网格生成以平面三角形网格生成技术为基础,其基本步骤为(图1-2-8):
(1)首先按在计算域内定义的网格尺度场,把边界离散成线段,并组成生成波[图1-2-8(a)]。
(2)从生成波中选长度最短的活动边,两端点为A和B。按背景网格上定义的网格尺度场生成点C,构成ΔABC[图1-2-8(b)]。
(3)在数据结构中,修改生成波。在图1-2-8(b)的情况下,AC和BC都是新的活动边,被纳入生成波;而AB则不再是活动边,被从生成波中删除。
(4)从活动边AC或BC出发,依相同方法生成另一个三角形,在图1-2-8(c)中,生成的是ΔBCD。
(5)将两个相邻三角形组合成一个四边形单元,在图1-2-8(c)中,ΔABC和ΔBCD就形成了四边形单元ABDC。
(6)以上过程重复进行,直到整个区域被四边形单元所覆盖。
(7)经单元形状优化,即形成可供有限单元计算用的网格。
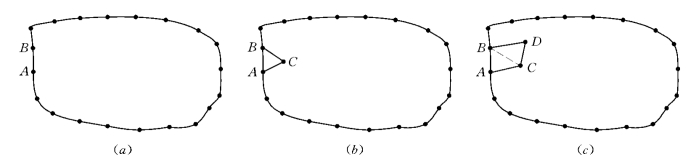
图1-2-8 平面四边形网格行波法生成过程(https://www.xing528.com)
四、曲面三角形网格的生成方法
曲面三角形网格生成同样也以平面三角形网格生成技术为基础,但曲面离散所生成的三角形单元必须满足{e}1、{e}2、{e}3三个方向的单元尺度要求(图1-2-9),同时三角形的3个顶点必须位于曲面上(Moller,Hansbo,1995)。
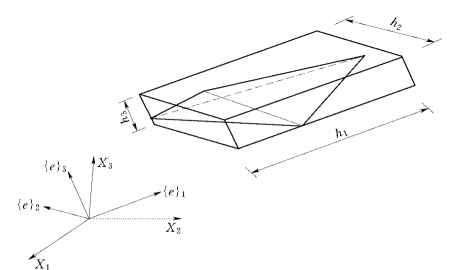
图1-2-9 曲面三角形单元尺度要求
曲面参数方程式(1-2-15)建立了曲面与参数面u—v的对应关系。一种直接的设想就是将曲面离散问题转化为参数面u—v上的离散问题。为此需在满足曲面方程约束的条件下,将对三维单元的尺度要求转化为对二维单元的尺度要求,然后在u—v平面生成平面网格Ω*,最后将Ω*投影至曲面,形成所要求的网格Ω。这个过程较为麻烦,因为不仅涉及尺度场之间的转换,而且还需生成具有方向性的三角形单元。为了克服这些缺点,可以将自然空间的曲面离散问题转化至正则空间处理。
先以二维问题为例说明。假定一平面X—Y内有三角形单元,其单元尺度由单位矢量({e}1,{e}2)和长度(h 1,h 2)来定义(图1-2-10)。规定变换如下:
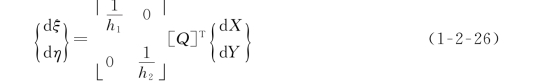
其中
![]()
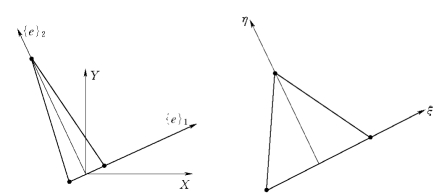
图1-2-10 自然空间至正则空间的转换
该变换由坐标系转动和延伸组合而成,将X—Y平面具有方向性的三角形变换至ξ—η平面的单位正三角形。
然后将讨论扩展至三维,令
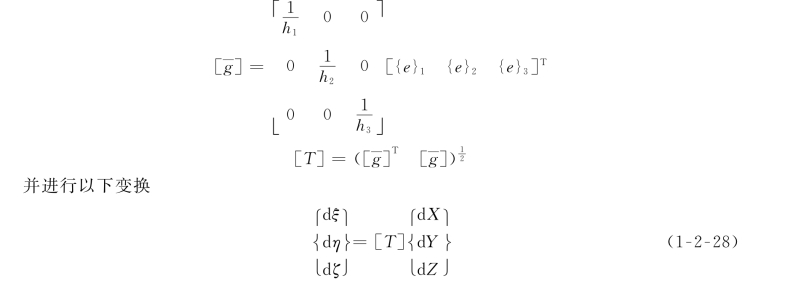
即可将三维曲面三角形单元转换至正则空间(ξ η ζ)。
Peraire等人(Peraire,Peiro,1992)将自然空间与正则空间之间的转换矩阵定义为

可以证明,[T]与[T′]实际上是一致的。[T]或[T′]所定义的变换消除了单元尺度方向性对网格生成的要求,把自然空间(X Y Z)内有方向特性的三角形转换为正则空间(ξ η ζ)内的等边单位三角形。
现考虑如何将正则空间中的三维曲面三角形划分问题转换为二维问题。根据式(1-2-15),有
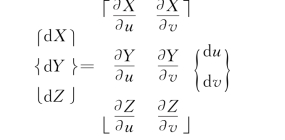
简记为
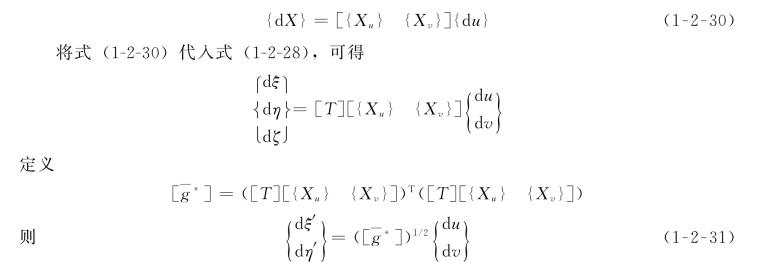
即把自然空间(X Y Z)内有方向特性的三角形转换为平面(ξ′ η′)内的等边单位三角形。
式(1-2-15)和式(1-2-31)分别定义了参数平面(u v)至自然空间(X Y Z)和参数平面(u v)至正则平面(ξ′ η′)的变换。正则平面(ξ′ η′)至参数平面(u v)的变换可记为

而自然空间(X Y Z)至参数平面(u v)的变换可以通过Newton迭代确定。在式(1-2-30)中,记
![]()
则由式(1-2-30)得到第k次迭代时,有
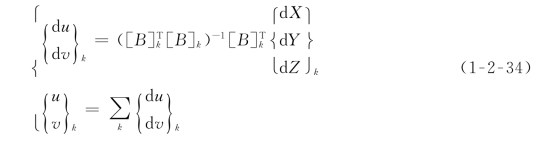
![]()

![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




