在岩体的变形与稳定分析中,渗流计算占有很重要的地位。
有限单元法被应用到渗流计算领域始于Zienkiewicz、Mayer和Cheung发表的求解拟调和微分方程的论文。从20世纪70年代开始,有限单元法相继扩展到求解随时间变化的非稳定渗流问题、非饱和渗流问题、裂隙岩体渗流问题以及渗流应力耦合问题(杜延龄,许国安,1992;毛昶熙,段祥宝,李祖贻,1999;张有天,2005)。
渗流问题有限单元法通常利用泛函的变分原理建立。
一、基本方程
根据Darcy定律及水流连续性条件,渗流的基本微分方程可表示为
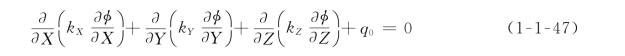
式中:φ为测压管水头;k X、k Y、k Z为三个主渗透系数;q 0为域内源密度。
对于稳定渗流,基本微分方程的定解条件仅为边界条件。
(1)第一类边界条件(Dirichlet)。当渗流区域的某一部分边界(图1-1-1中的边界Γ1)上的水头已知时,边界条件为
![]()
(2)第二类边界条件(Neumann)。当渗流区域的某一部分边界(图1-1-1中的边界Γ2)上的法向流速已知时,边界条件为

图1-1-1 渗流问题边界条件


把式(1-1-53)代入式(1-1-52),然后令式(1-1-52)的变分为零,可得用有限单元法求解渗流场的方程组为
![]()
式中:[H]为整体传导矩阵,由单元传导矩阵[h]e集合而成;{Q}为自由项向量,来自于域内源和已知边界流量的贡献,由{Q}e集合而成。

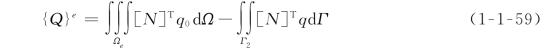
与应力应变分析相比,式(1-1-59)右端第1项相当于体积力引起的结点荷载,第2项相当于边界上表面力引起的结点荷载。对于有压渗流问题,只需一次性求解方程(1-1-54)即可;对于无压渗流问题,由于自由面和逸出点均未知,故需进行迭代求解。
二、无压渗流自由面的计算
自由面是渗流场特有的一个待定边界,需要采用网格修正法或固定网格法迭代确定。网格修正法将自由面当作可变边界处理,在迭代过程中反复修改自由面位置,使网格发生相应变形,直到自由面位置稳定为止(France,Parekh,Peters,1971;魏泽光,黄俊,许国安,李春华,1982)。网格修正法应用不便,目前常采用固定网格法。自从Neumann(1973)提出求解有自由面渗流问题的Galerkin法以后,不少学者对固定网格法进行了研究,比较有影响的有Desai(1976)的剩余流量法、Bathe(1979)的单元渗透矩阵调整法、张有天等人的初流量法(张有天,陈平,王镭,1988)、速宝玉等人的虚流量法和截止负压法(速宝玉,朱岳明,1991;速宝玉,沈振中,赵坚,1996)、吴梦喜等人的虚单元法(吴梦喜,张学勤,1994)等。这些方法各有特点,共同的优点是可以保持网格不变,程序处理简单。
1.网格修正法
首先根据经验假定渗流自由面的位置,然后把它作为一个计算边界,按照v n=0的边界条件进行分析,得出各结点的φ值后,再校核φ=Z的条件是否满足。如不满足,则调整自由面和渗出点的位置,再求解。
网格修正法的优点是:渗流自由面和逸出点可以随着求解渗流场的迭代过程逐步稳定而自行形成,迭代过程是收敛的。但是网格修正法具有明显的缺点:对有复杂结构面系统和复杂排水系统的结构应用较困难;对渗流自由面位置的初始假定要求较高,如果初始自由面与最终自由面位置相差较远,则极易造成单元畸变,影响计算的精度;由于网格变形,整体传导矩阵需要重新形成;渗流与应力耦合分析无法在同一网格下进行。
2.剩余流量法
剩余流量法首先由Desai(1976)提出。剩余流量法通过不断求解流过自由面的法向流量(称为剩余流量)建立求解水头增量的线性代数方程组,以修正全场水头和调整自由面位置。迭代过程中只需一次形成整体渗透矩阵,但需要判断自由面被单元分割的各种情形,要求算出自由面被单元切割的面积及流过自由面的法向流速,计算工作量较大。剩余流量法的全部调整均基于第一次有限单元计算的结果,因而计算精度较差,收敛速度慢。剩余流量法的计算步骤如下:
(1)对所研究的渗流域进行全域划分,根据式(1-1-54)及第一类边界条件,求得水头的近似值{φr}。
(2)根据φr=Z的条件,确定渗流自由面位置。
(3)计算第r次迭代时渗流自由面上法向流速v nr及结点剩余流量{Qr},即
![]()
 (https://www.xing528.com)
(https://www.xing528.com)
式中:{l}为自由面的单位法线向量。
(4)以{Qr}作为控制方程的右端项,求解方程
![]()
(5)求解第r次迭代后的水头值,即
![]()
(6)若{Δφr}充分小,则停止迭代,否则令r=r+1,转至步骤(2)。
3.单元渗透矩阵调整法
单元渗透矩阵调整法首先由Bathe(1979)提出。根据单元结点水头与结点位置势的比较,对渗流场进行分区,各区的渗透系数给不同的值,通过不断调整单元渗透矩阵,模拟渗流不饱和区的作用,以确定渗流饱和区及渗流场。该算法的实质是把边界不确定的非线性问题转化成材料非线性问题。
该法也需每次迭代求出自由面的位置,再求出被自由面穿越单元的水上、水下部分的体积。水上部分的渗透系数取k/1000,水下部分的渗透系数取实际值k,在介于水上和水下部分的界面出现渗透系数跳跃的现象。在确定被自由面穿越单元的水上、水下部分的体积时,需先确定自由面与单元的切割情况,并判断被切割部分的几何形状。
单元渗透矩阵调整法的改进方法主要有复合材料单元法和加密高斯点法。
复合材料单元法在水上部分取渗透系数为实际渗透系数的1/1000,在水下部分取实际渗透系数,在介于水上和水下部分的界面的一个不大的邻域(-ε,ε)内,用连接该邻域端点的渗透系数值作一线性函数过渡,避免含自由面单元的复合缝面处由于渗透系数发生突变而影响收敛的稳定性。
加密高斯点法则试图更精确地计算含自由面单元对渗透矩阵的贡献。
4.初流量法
初流量法由张有天等人提出(张有天,陈平,王镭,1988)。该法利用高斯点的水头求出结点的初流量作为求解水头增量的右端项,避免了自由面与单元切割的计算。初流量法的计算步骤如下:
(1)对所研究的渗流域进行全域剖分,根据式(1-1-54)及第一类边界条件,求得水头的近似值{φr}。
(2)据φr=Z的条件,确定渗流自由面位置。根据高斯点的水头值进行判断:若φr<Z,则表明该高斯点位于自由面以上;若φr>Z,则表明该高斯点位于自由面以下。于是可以确定渗流自由面的初始位置。
(3)对每个包含自由面的单元,逐个计算高斯点水头,当φr<Z时,通过式(1-1-65)计算该高斯点对该单元结点流量的贡献,即

(4)依次对φr<Z的所有高斯点求得各结点的累计结点初流量{Qr},以其为右端项按式(1-1-66)求结点的水头增量,即
![]()
(5)则第r次迭代后的水头为
![]()
(6)若{Δφr}充分小,则停止迭代,否则令r=r+1,转至步骤(2)。
三、无压渗流逸出点的计算
逸出点在渗流自由面和逸出面的交界处,可以作为渗流自由面的未知水头结点,又可以作为逸出面的已知水头结点,确定方法有以下几种:
(1)和渗流自由面上的结点一样,作为未知水头结点,通过计算来确定其位置,但修改调整逸出点的位置时需沿着逸出面进行。
(2)作为已知水头结点,通过计算求出渗流自由面上其他各结点的水头值,然后调整自由面。逸出点的位置则根据与其邻近的自由面上结点的位置来修改。
(3)将逸出面转化成第二类边界处理。在第r次迭代计算时,可求出逸出面单元外表面的法向流速v nr,在第r+1次迭代时,通过下式将其转化为第二类边界。

式(1-1-68)中,{Q}e即为式(1-1-54)中的右端列向量。
四、渗透体积力的计算
渗流分析的任务之一是计算渗流荷载,作为评价岩体变形和稳定性的依据。渗透体积力在单元结点上引起的等效结点力为
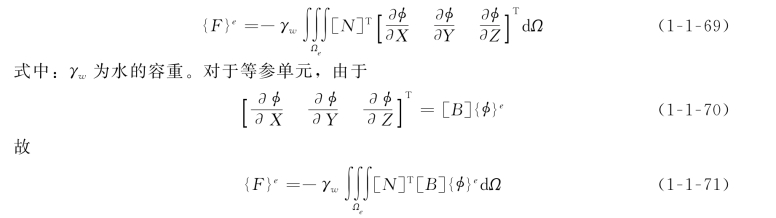
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




