战斗部破片飞散特性详解

配用近感引信的弹药主要是杀伤榴弹或导弹破片型战斗部。杀伤目标主要利用的是爆炸产生的破片杀伤作用。决定杀伤榴弹或破片型战斗部杀伤作用效率的因素有：弹丸（战斗部）爆炸形成的破片数、破片质量、破片飞散角、破片速度和破片在飞散角内的分布密度。

一、破片静态飞散特性

弹丸（战斗部）静止爆炸时，其破片在空间的飞散区称为破片静态飞散区，通常战斗部破片静态飞散区具有轴向对称性，即破片静态飞散随飞散角度的密度分布绕弹轴Oxm是对称的，因此，破片飞散密度只是破片飞散方向与战斗部纵轴的夹角φ的函数

K（φ）曲线一般由地面多发静态爆炸试验统计获得。K（φ）分布曲线通常具有类似图11-11所示形式。

图中φ0为静态飞散中心方向角，即破片平均飞散方向与弹轴之夹角；Δφ为静态飞散角，通常指90%破片所占的飞散角宽度。

破片静态飞散初速v0具有一定的变化范围，并随飞散方向角φ而变化，v0随φ变化一般由静态试验来确定，通常具有图11-12所示形式。

图11-11　战斗部破片静态飞散随角度的密度分布

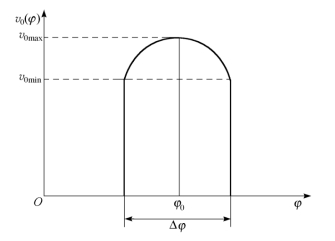
图11-12　破片静态飞散初速度随角度的变化v0（φ）

通常在计算中不考虑初速度随角度变化，而取其平均值。如v0变化太大，则必须考虑其变化对动态飞散的影响。

二、破片动态飞散区

战斗部破片动态飞散区是指在遭遇点爆炸时破片相对运动的飞散区域。破片相对运动速度是破片本身的静态飞散速度和弹目相对运动速度之合成速度。由于破片有效杀伤距离相对不大，故在分析破片动态飞散区时通常忽略破片在空气中的速度衰减。

战斗部破片动态飞散速度向量v0r的合成图如图11-13所示。图中vr为导弹与目标的相对速度，vrxm、vrym、vrzm为相对速度在弹体坐标系中三个分量。

图11-13　战斗部破片动态飞散角及飞散速度

设在弹体坐标系内某一方位β上的一个破片，其相对运动速度为向量v0r，则

v0r＝v0(β0)＋vr

式中，v0为静态飞散角为β0的破片初速向量；β为v0r向量在ymzm平面上动态飞散方位角；v0（β）为在ym、zm平面上的分量，其速度向量合成如图11-14所示。

从图11-14可看出：

v0r在xm轴上的投影为

破片的动态飞散方向角Ω在弹体坐标系内为

在β方向上破片动态飞散初速v0r（β）为

由于相对速度向量vr相对弹轴Oxm不对称，故战斗部破片动态飞散方向角Ω及动态飞散速度v0r相对弹轴亦不对称，即Ω和v0r均为飞散方位角β的函数，Ω（β）随β的变化如图11-15所示。

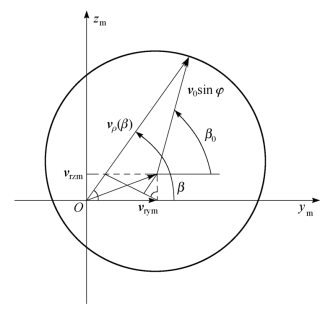
图11-14　vρ（β）速度的合成

图11-15　战斗部破片动态飞散方向角随β的变化

图中Ω0（β）为对应静态飞散中心方向角φ＝φ0的动态飞散方向角；Ω1（β）为对应静态飞散中心方向角φ＝φ＋Δφ/2的动态飞散方向角；Δφ为破片动态飞散角的宽度。

三、动态飞散密度分布

破片动态飞散密度分布函数是单位动态飞散角中破片的百分数，已知静态密度分布函数就可以求出相应的动态密度分布函数。(www.xing528.com)

这里主要讲破片动态飞散密度分布在弹体坐标系中的表示法。

设φ、Ω分别为破片静态和动态飞散方向角，则动态密度分布为破片百分数对Ω的导数

K（φ）为式（11-45）所定义的破片静态飞散密度分布函数。先假设破片初速为常数v0，然后对式（11-48）两边进行微分得

由此得

其中

已知动态飞散方向角，vr的三个分量vrxm、vrym、vrzm及静态飞散方向角φ，就可根据上面式（11-50）、式（11-52）、式（11-53）求出战斗部破片动态飞散密度分布函数dN/dΩ。但在实际计算中目标要害方向β、Ω为已知，而静态飞散方向角φ为未知，此时首先需根据β及Ω值求出φ角。为此联立式（11-46）、式（11-47）、式（11-48）就可解出

其中

有了φ角求得静态飞散密度K（φ）及dΩ/dφ值，也就可以求得破片动态飞散密度分布函数dN/dΩ。动态及其相应的静态飞散密度分布函数如图11-16所示。

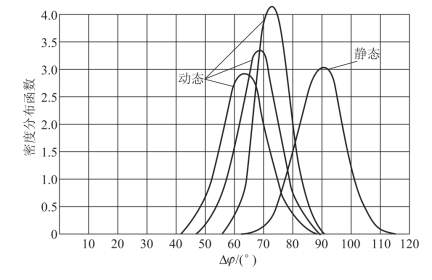
图11-16　破片动态飞散密度分布函数

图中取v0＝3 000m/s，vr＝1 000m/s，Ωr＝30°，φ0＝90°，Δφ＝30°，K（φ）取正态分布。

动态飞散角要比静态飞散角窄，即dφ/dΩ＞1，因此，动态飞散密度比相应的静态飞散密度要大。

四、目标要害部位命中破片数

设目标上共有j＝1，2，…，jmax个要害部位，第j个要害部位中心在目标坐标系中的坐标为（Xtj、Ytj、Ztj），如变换到弹体坐标系中坐标为（Xmj、Ymj、Zmj），就可以确定在战斗部爆炸时，第j个要害部位中心在弹体坐标系内的方向角βj、要害方向与Xm轴夹角Ωj以及要害部位中心离战斗部中心的距离Rj。

第j个要害部位与战斗部破片飞散的空心圆锥相切的圆环面积上击中的破片数为

式中，Uj为面密度；Sj为圆环面积，如图11-17所示。

dS＝2πRjsinΩjRjdΩ

将dS代入Uj，可得

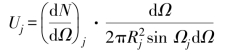
将式（11-50）代入上式得

设N0为破片总数，破片飞散空心圆锥所切圆环面积为Sj，则得到圆环面积上的破片数为

因为式K（φj）的单位是百分数/弧度，故变为角度求破片数需乘以57.3/100。

图11-17　圆环面积