二维静电场的矢量探测理论与方法

首先介绍二维静电场矢量探测理论与方法。如图9-11所示，假设在二维平面区域M中存在一个匀强静电场E。在该静电场中建立如图的坐标系XOY，然后在该静电场中布设两对电极板：A极板和B极板的板面垂直于X轴，之间距离为a，对称于Y轴，C极板和D极板的板面垂直于Y轴，之间距离为b，对称于X轴。为论述方便，定义极板间距为处于同一坐标轴上一对极板间的距离。

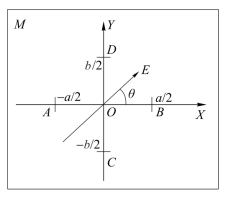
图9-11　求解二维匀强电场场强方向原理图

由于电场的作用，在A、B极板之间和C、D极板之间会产生电势差。设在A、B极板间产生的电势差为UAB，在C、D极板间产生的电势差为UCD。

其中LAB、LCD是沿AB、CD的有向线段矢量。

由式（9-34）和式（9-35）可得：

式中，eR是沿电场强度方向的单位矢量。

根据图所示的几何关系，式（9-36）和式（9-37）可以用标量式描述为：

如果测得UAB和UCD，并且取a＝b，则可求出区域M内的静电场强度。

把这种求解静电场场强大小和方向的方法称为静电场矢量探测法。

由此可得出定义：静电场矢量探测方法是指基于静电场的矢量特性，利用正交放置的静电探测极板测量得到的电位差来求解静电场场强大小和方位的方法。此法主要用于对空弹药引信对空中静电目标的探测。

(www.xing528.com)

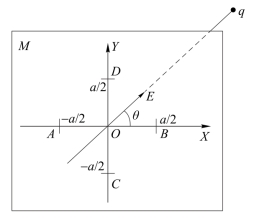
图9-12　求解二维空间点电荷方位原理图

另外，把用来进行静电场矢量探测的四个电极构成的探测系统称为静电场矢量探测器。为便于后续讨论，把图中探测电极A、B电极连线定义为静电矢量探测器的方位轴：探测器判定场强方向以此线为基准位置。在此基础上讨论二维空间点电荷的方位探测原理。

如图9-12所示，如果在二维空间有一个携带电量为q的点电荷，在距离此电荷足够远处的区域M中，布设与图中位置相同的四个探测电极，并建立相同的直角坐标系XOY。设坐标原点到点电荷的距离为R，由静电场理论知电场强度满足：

此处eR是沿电场强度方向的单位矢量，电场强度的矢量方向如图9-12所示。

当区域M足够小、且坐标原点到点电荷的距离足够大时，可以认为区域M中的静电场近似为匀强场。根据上一节关于匀强电场的求解方法，将可以判断点电荷相对于坐标原点的方位角。

根据式（9-38）～式（9-39）可得：

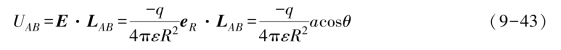
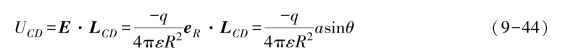
因此可以计算出此时点电荷的方位：

如果测得UAB和UCD，则可以通过求取θ确定静电场的方向。

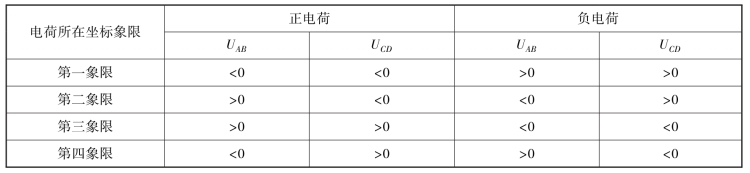
当然，由于三角函数存在周期性，通过式（9-45）并不能在0°～360°范围内唯一确定θ。在图9-12所示坐标系中，不同极性电荷形成静电场引起的电位差UAB和UCD的符号也不同，据此可以判断点电荷所在坐标象限，如表9-1所示。

表9-1　极板电势差符号与点电荷位置关系表

即可在0°～360°范围内唯一确定θ值，求解场强的方向。