静电探测原理及应用解析

静电感应起电理论指出，当带电体附近有一金属导体时，金属导体离物体接近的一端感应出与带电体极性相反的电荷，另一端感应出等量异号的电荷，如图9-1所示。

图9-1　感应起电原理图

这里假定带电体O和金属导体M悬浮在空中，且O带正电荷Q，导体M两端感应的电荷为-q和＋q。那么，在导体M靠近带电体O一端的表面附近任一点P的法向电场Ean，将由带电体O的电场En和金属导体M电场Em的共同叠加形成，即：　

此外，如果金属导体除感应电荷以外，自身还有净电荷q0，则P点的合成场强还应包含自身净电荷q0产生的电场分量El，那么此时的合成场强为：

根据高斯定理，可得出P点附近金属导体M表面的电荷密度为：

式中，ε0为空气的介电常数。

则金属导体M靠近带电体一侧所带的异号电荷总量为：

其中，S为金属导体带异号电荷的面积。

与带电体所带电量异号的总电荷量-q是在带电体的作用下产生的，其大小和带电体所带电荷量紧密相关，因此可以通过检测电荷量-q的大小及变化来获取目标的信息。

图9-2　静电引信探测电极原理图

在近感引信中，通常将用于产生感应电荷的金属导体定义为探测电极。单一电极的感应电荷是无法检测的，一般采用双电极，如图9-2所示。另一极常为弹体，同时作为探测电路参考地。令两电极间的电容为C，两电极间的电压差为U，则两电极间的电荷为q＝CU。

因此，检测两电极间的电压差即可获得感应电荷的信息，从而得到目标的信息。但是在静电引信的使用场合，两电极间的感应电荷的电压差非常微弱，这对用于信号放大的运算放大器提出了极高的要求。另一种可选的方法是采用电荷放大器检测电极间的感应电荷q。对电荷放大器而言，通常需要求输入阻抗≥1014Ω以上。这些要求，在引信工作的恶劣环境中较难得到保证。

如果在两电极间连接一个取样电阻，当带电体电场变化引起电极的感应电荷发生变化时，电荷从取样电阻流过，通过检测这一微弱电流，可获得目标电场变化的信息。根据式（9-11），有：

将式（9-9）代入式（9-12）中，有：

对于金属导体感应电荷产生的电场，和目标电荷在该处的电场有如下关系：

式中的系数K（G，r）是由参数G和r确定的非线性函数，G为静电引信弹体和电极的形状、体积决定的几何参数，r为弹目间距离。当弹目间逐渐接近时，K（G，r）随之变化。然而，K（G，r）的值远远小于1，可得Em≪En，为了理论分析的方便，忽略K（G，r）随时间的非线性变化，即令K（G，r）为仅与弹体参数相关的某一常量：

则式（9-13）变为：

对于El项在静电引信中是由弹体自身带电产生的，即弹丸在飞行中因各种因素产生的静电荷。弹丸自身的电荷在弹丸脱离炮口以后很短的时间内即达到平衡，弹体的电荷保持不变；在弹丸和目标交会过程这一短暂时间中，可认为弹体自身的电荷同样保持恒定。这样，在弹目交会过程中弹丸自身带电的电荷的场强为常量，式（9-16）中第二项可视为零，即有关系：

上式即是感应电荷在电极间移动所产生的电流信号表达式。通过检测移动的电荷量，即感应电流的大小来获取目标的信息，将这种探测方式命名为检测电流式静电探测。由于微弱电流检测技术和集成电路芯片工艺技术较成熟，所以检测电流法更适合静电引信使用。式（9-17）即是检测电流式被动静电引信的电场作用公式，从该式可得到如下推论：

①当为零时，没有信号输出。即这种静电探测器对不带电目标以及弹目间无电场扰动的情况，无信号输出；此外，输出信号的大小取决于电场变化的大小，而不是电场的绝对值大小。所以，静电引信将能有效克服其他体制近感引信面临的各种电磁对抗和光谱对抗等问题。

②同样的电场分布情况下，弹目接近速度越大，即相同的ΔE变化量，Δt越小，电场的变化量越大，输出信号也越强。利用这一性质，可以用实验室模拟弹目交会的结果，推导实际弹目交会速度情况下可能的探测距离。

③同样的弹目交会速度下，目标电场梯度越大，即Δt不变，ΔE变化越大，越大，输出信号越强。通常，曲率越大的形状体附近，电场梯度越大。利用这一性质，可获得目标形状的一些信息，并以之作为目标识别和抗干扰的部分依据。

④在电极形状确定的情况下，探测电极面积S越大，产生电荷的积分区域越大，输出信号越强。

⑤电极各点感应的电场强度随电极的位置而变化。利用这一性质，可采用多电极环布引信的四周，以排除带电云层等空间均匀分布电场的干扰。

⑥由于弹体自身带电产生的电荷在弹目交会过程中的变化量很小，自身荷电产生的检测电流近似为零，即这种检测方式不受弹体累积电荷的影响。

式（9-17）从静电场的角度得出了检测信号与目标电场的关系，为从目标电场分析信号的目标特性提供了途径。为了给静电引信探测器的设计提供依据，根据图9-2中目标、环境和引信三者关系，从电路的角度建立如图9-3的探测系统电路模型。从图中可以看到，目标和探测电极间等效电容为C1；探测电极与参考地之间的等效电容为C2，两电极间的等效电阻为R；目标和参考地电极间的等效电容为C3。图9-4为其等效电路图。(www.xing528.com)

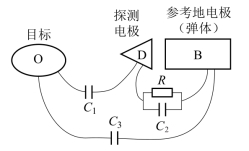
图9-3　探测系统电路模型图

图9-4　探测系统等效电路图

电路中，C2的电容包括两电极形成的电容、导线电容和元器件连线及引脚电容。由于电极电容远大于后两者，为分析的方便忽略后两者的影响而仅认为C2是电极电容。同样，总电阻R也只考虑占主要作用的连于两电极间的电流检测电阻。

目标、引信探测电极、引信参考地之间分别存在电势差，将目标和引信参考地之间的电势差记为Ui，将目标和引信探测电极间的电势差记为U1，引信探测电极与参考地之间的电势差记为U2。当弹目间有相对运动时，目标、探测电极和参考地之间的电势差发生变化，从而导致探测电极的电荷发生变化，由于电容存在容抗，其作用可等效为有电流从目标流向探测电极，即充电电流从C1流过，令电流为i1。同样，可令流过电容C2的电流为i2，流过电阻R的电流为i，电阻R两端的电压为Uo。根据频域分析理论和电路分析方法，有如下关系：

可得到探测电路输出与目标和参考地间电位差的传递函数为：

探测系统的模型可简化为如图9-5所示。

图9-5　探测系统简化模型图

系统的输入为Ui，弹目接近过程中，目标到弹体参考地电位的变化代表了这一过程中的目标电场变化规律。探测系统的输出为探测电路电流检测电阻两端的电压输出。系统传递函数就是从目标到电路输出端所有作用环节的总和。

式（9-19）中，C1是由弹目间位置、距离和弹目间介质特性所共同决定的；C2为引信探测电极和弹体之间的电容，表征了引信电极间的关系；R为电流检测电阻，为探测电路的重要参数。可见，探测公式完全包含了目标、环境和引信的相互关系，为分析目标特性及其与环境关系和设计探测系统提供了基本途径。

从式（9-19）可以得到探测系统传递函数的相频响应为：

被动式静电引信的目标信号的频率一般较低，电容和电阻的变化引起的相位变化相当微弱，所以可以忽略不计。

从式（9-19）可以得到探测系统传递函数的幅频响应为：

根据此式，可推导得到如下结论：

①增大C1，探测系统传递函数增益增加。

将式（9-21）中C1变换到分母中，可得到

在其他条件不便的情况下，增大C1，增大，即同样输入下探测系统有更大的输出响应。

由于探测电极与飞机间的形状和结构复杂，弹目间的交会情况也千变万化，很难用具体的表达式描述弹目交会过程中电容的变化。但是根据电动力学理论可知，电容的大小与电极间的面积S1成正比，与电极间介质的介电常数也成正比，与距离成反比，因此可定性地描述为：

k1为和电极、飞机形状结构及其相互位置有关的因数。

根据式（9-23）可知，探测电极与目标间的等效电极面积S1越大，电容C1就越大，因此探测系统增益越大；与环境温度、湿度及气压等因素有关的环境介质介电常数ε0也和探测系统增益成正比。这和场强模型的探测公式反映的这一规律一致。

②减小C2，探测系统传递函数增益增大。

从式（9-22）可以直接看出，当探测电极和弹体间的电容C2减小时，系统增益增大。C2的值由非规则形状的电极和弹体决定，同样不能用表达式来描述。采用经验公式有

k2为与电极和弹体相互关系有关的因数。

增大探测电极和弹体间的距离d2可减小C2，增大探测系统增益。同时，两电极间的介电常数ε2要尽量小，因此电极表面的绝缘介质介电常数应选择参数较小的物质。

③电流检测电阻R增大，探测系统传递函数增益增大。

将式（9-21）中分子分母同除以电阻R，有如下式：

当电阻R增大时，系统增益增加。但是当R的值过大时，探测系统的弛豫时间常量τ＝RC与弹目交会的有效作用时间时相比处于同一数量级或更大时，电阻R上流过的电流反映不出弹目交会时电极感应电荷的变化。通常保证时间常量τ在μs数量级，让探测系统的响应和目标交会具有实时的对应关系。

以上即为电流检测式被动静电引信探测原理及电路模型，根据上述分析可设计出高增益的探测电路及探测电极。