距离方程及其应用于结构辐射计中的影响因素

被动锥扫辐射计的简化方框图如图6-13所示。可以导出这种结构辐射计的距离方程，其中包括适当考虑锥扫调制对信噪比的影响。

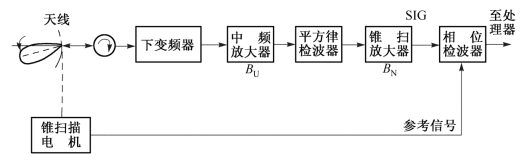
图6-13　被动锥扫辐射计方框图

可以这样认为：天线末端的总功率是天线接收到的信号功率与折算到天线末端的接收机噪声功率之和。这两种功率源都可以与等效噪声温度联系起来，称总的温度为辐射计工作温度（tsy）。对于超外差接收机来说，有

式中，ta为天线温度；trn为接收机噪声温度，trn＝（F-1）t0，F是系统的噪声系数，t0是标准噪声温度，典型值为290K；因子2是镜像响应造成的。

天线接收的带宽功率的统计特性与接收机噪声的统计特性是一样的，它们在射频带宽内都是白的，即均匀的功率谱。若取tsy为折算到天线末端的辐射计的工作温度，则平方律检波器输入端的功率密度为

式中，k为波耳兹曼常数；G为射频、混频以及中频部分的总增益。当系统处于常值工作温度，平方律检波器产生一个直流和一个交流起伏功率输出。

在全功率辐射计中，信号功率就是输出功率中的交流部分，它是在2BN输出双边带内的噪声变化部分，其中因子2是由于镜像的影响。全功率辐射计的信噪比（平方律检波输出的信噪比）为

式中，2Δta＝Δtsy为系统温度的变化量；BN为扫描频率放大器带宽；Bif为中频放大器带宽。

设Kr为辐射计工作类型常数，则式（6-46）可以表示为

根据式（6-47）也可以导出辐射计灵敏度，即使S/N＝1，则可求出最小检测的均方根温度Δta值。由式（6-47）有

方程（6-48）为辐射计灵敏度的一般表达式，Kr由辐射计类型及信号处理形式确定。全功率辐射计的Kr为。

辐射计通过观测天线温度的变化Δta而检测出目标。因此，可将Δta与目标的辐射温度反差ΔtT联系起来。即

(www.xing528.com)

式中，ηa为天线的辐射效率；ΩT是目标对着的立体角；ΩA是天线的等效立体角（包括旁瓣效应）。天线立体角可写为

式中，ηA为天线口径效率；ηB是波束效率；D是天线口径直径；ΩM是主波束立体角。

目标实际投影面积AT对应的立体角可用距离R来表示，即

根据式（6-47）、式（6-49）、式（6-50）和式（6-51）并代入接收机的噪声系数，可以给出距离方程如下

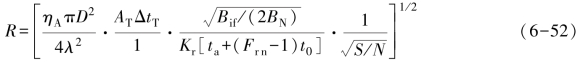
式中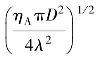，为天线参数对作用距离的影响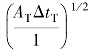；为目标参数对作用距离的影响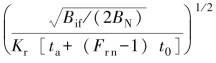；为辐射计参数对作用距离的影响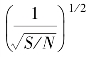；为平方律检波输出信噪比对作用距离的影响。

根据式（6-50）可得

把式（6-48）和式（6-53）代入式（6-52）可得到距离方程的简单形式

这也是人们常用的一种形式。

从距离方程可以看出以下几点：

（1）作用距离直接随天线直径和工作频率的增大而增大（不考虑大气衰减）；

（2）中频放大器的性能以其带宽的1/4次方影响作用距离；

（3）作用距离反比于接收机噪声系数的平方根；

（4）作用距离相对输出带宽中的信噪比不敏感。