反相关噪声引信的运作原理：简介与优化方法

反相关噪声引信采用反相关法接收。图5-10所示是反相关接收机的方框图。由反相关接收机的输出端形成以反相关函数表示的信号。

图5-10　反相关接收机的方框图

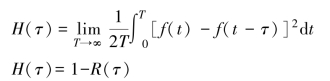
由上式可知，在τ＝0（即距离R＝0时）时，反相关电路的输出为零，随着τ的增大输出随之增加，能直接按照接收机输出信号的相应值确定目标距离。减小了发射机到接收机泄漏的影响，克服了自相关噪声引信的缺点。

下面介绍一种噪声调频反相关引信原理。假定发射信号为一低频噪声调频的调频波，则混频器的输出为基准信号与回波信号的差频信号，其差频

Δω＝ω(t)-ω(t-τ)

如果发射信号是被一个振幅为高斯分布的低频随机噪声信号f（t）调频，当发射机的频偏特性是线性时，则发射信号的频率分布是以载频ω0为中心频率的高斯分布。因此，频差Δω也是以零频率为中心的高斯概率分布。由于混频器不能保持频差的代数符号，所以混频器输出的瞬时频差只能是单向的高斯概率分布，并且在零频时具有最大值。由于Δω有N（0，σ）分布，则有一般的反射正态分布，而且其k阶矩为

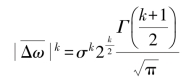
式中，σ为标准差，；为Gamma函数。

当k＝1时，Δω的平均值与均方值（Δω）2的关系由上式可得

如果f（t）是归一化的，则有

f(t)＝ω(t)/ω(t)rms

式中，ω（t）为瞬时频偏，ω（t）rms为均方差。

由于

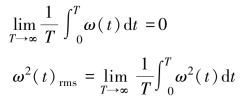(www.xing528.com)

所以归一化的反相关函数为

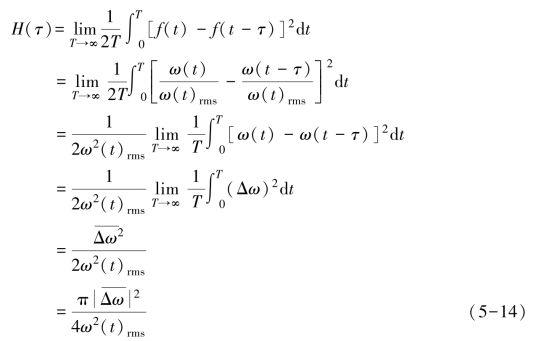
由式（5-5）及式（5-11）可得

式中，R（τ）和G（f）分别为低频噪声的归一化相关函数和功率谱密度。由式（5-14）及式（5-15）可得

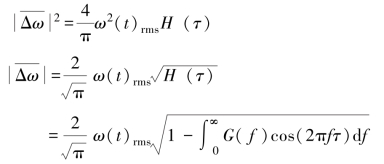
令

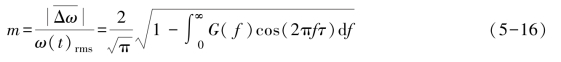
m称为频差的标准平均值，也可称为归一化的差频平均值。

由上式可见，延迟时间τ增加（即弹目间距离R增加），相关函数R（τ）下降，反相关函数H（τ）增加，因而差频是随回波延迟时间τ的变化而变化的。τ与距离R相对应，所以通过测定或者就可以直接得出距离。选择适当的低频噪声频谱G（f），可以使系统的频差标准平均值m与距离R是单调上升的。在实际系统中，可以设计出测量或者的装置。

图5-11给出了利用来测距的原理方框图。噪声产生器具有零平均振幅的高斯分布噪声，这种白噪声通过线性频率形成网络，获得具有适当频谱的噪声调制信号。噪声调制信号对发射机进行线性频率调制，使发射机输出噪声调频波。从发射天线辐射的能量被目标反射回来，通过接收天线接收。发射信号和接收信号经过混频器输出差频Δω信号，进入放大与限幅器。限幅器限幅后得出差频的平均值，当鉴频器的输出达到对应于预定的目标距离时，判别电路就输出启动信号，使执行级工作。

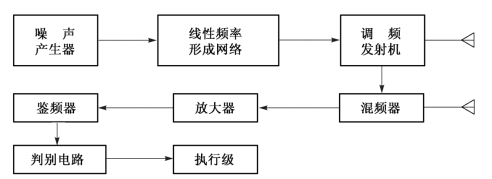
图5-11　利用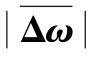测距的原理方框图

图5-12给出了利用来测距的原理方框图。从图中可见，以低频带通及检波器代替图5-11中的线性鉴频器，其他部分与图5-11相同。混频器输出的信号，经放大与限幅后，用低通滤波器提取一定频带内的低频区域信号，该低频信号的能量可以代表频率的方差值，经过检波后输出的信号便可以指示距离。

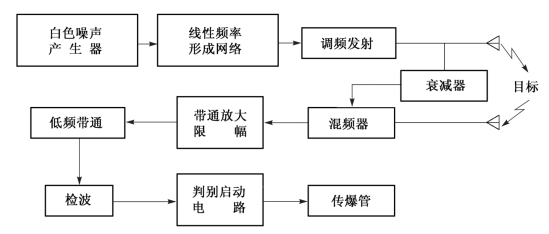
图5-12　利用　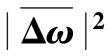测距的原理方框图