常见的噪声谱和自相关函数

在研究噪声时，通常按其概率密度和功率谱的形状来分类。如按功率谱的形状分类时，可将噪声分成白噪声和有色噪声。白噪声是一种理想化模型，它的电压（电流）瞬时值的概率分布是高斯分布，对于平均值为零的白噪声电压瞬时值的概率分布密度表示为

式中，σ2为随机噪声u的方差，即噪声的有效功率（指在值为1Ω的电阻上的平均值）；σ为随机噪声u的均方根偏差，或称为标准差，也就是噪声电压的有效值。

噪声电压的波形图和概率密度曲线如图5-1所示。图（a）是将时间轴扩大了的噪声电压波形图。图（b）是噪声电压的概率密度曲线（即正态分布曲线），它表明噪声电压的振幅分布特性主要取决于噪声电压有效值的σ。随着σ的增大，噪声电压较大的尖头脉冲出现的概率增大，同时，电压较小的尖头脉冲出现的概率相应地减小。电压小于σ的概率为68.3%，小于2σ的概率为95.6%，小于3σ的概率为99.7%，也就是说噪声电压大于3σ的概率是极小的。

由于白噪声是许多极其短促的、相互独立的、统计无关的电压（电流）脉冲加在一起组成的，每个短促脉冲所占频谱是很宽的。所以白噪声的频谱可以看做均匀的无限频谱，即噪声功率在整个频谱内是均匀连续分布的。它的功率谱密度G（f）为常数，即G（f）＝N0（常数）。

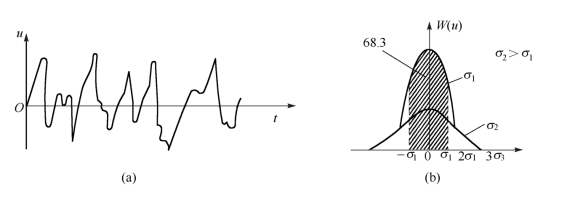
图5-1　噪声电压波形和概率密度曲线

（a）将时间轴扩大了的噪声电压波形；（b）噪声电压的概率密度曲线

由式（5-7）可得

式中，δ（τ）为单位冲量函数（狄拉克函数）；G（f）及R（τ）如图5-2所示。这个结果表明，白噪声只在τ＝0时是相关的，除此之外，τ为任意值时都是不相关的。而实际上，噪声功率密度不可能在所有频率范围内为一常数，因为这意味着噪声有无限大的功率，而噪声功率总是有限的，所以实际的噪声频谱有限。但由于无线电引信的带宽是较窄的，在这个带内，可把噪声频谱看成一常数。

图5-2　功率谱密度G（f）及相关函数R（τ）

为了得到合适的相关函数，往往采用特殊办法形成相应的噪声功率谱密度，下面考虑几种特殊情况的噪声功率谱密度，并求出对应的相关函数。

一、白噪声通过一个理想带通滤波器

白噪声通过理想带通滤波器输出的功率谱如图5-3所示。其归一化的功率谱密度为

将上式代入式（5-11）并积分可得相关函数为

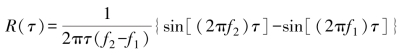
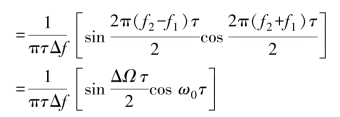
式中，ΔΩ＝2πΔf，ω0＝2π（f1＋f2）/2，R（τ）和τ的关系如图5-4所示，是一个包络为脉冲函数的余弦振荡。τ0定义为第一个零点出现的时间，即

也就是Δfτ0＝1，因而。

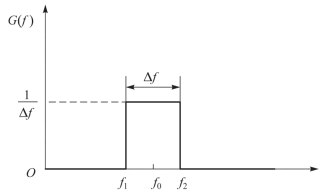
图5-3　白噪声通过理想带通滤波器输出的功率谱密度

图5-4　白噪声通过理想带通滤波器输出频谱的相关函数(www.xing528.com)

相关时间τ0表明起伏噪声内在联系的紧密程度。τ0不同，说明起伏过程快慢不同。对于无穷频谱的白噪声，τ0＝0表示噪声变化极为迅速。对于有限带宽的白噪声，τ0≠0，其变化就慢一些。对于窄带噪声，包络变化的速度与噪声带宽Δf成反比，带宽越窄，则其输出的噪声包络变化越缓慢，包络的结构越松散。

二、白噪声通过一个理想低通滤波器

当f1＝0，f2＝F0时为理想低通滤波器，这时输出噪声的功率谱密度为

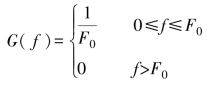
相关函数为

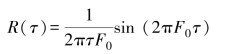
G（f）与R（τ）的图形如图5-5所示。R（τ）随τ的增大而衰减振荡，R（τ）与τ是非单值关系，一个R（τ）可对应于多个τ值。

三、白噪声通过一个低通RC滤波器

低通滤波器如图5-6所示。假设噪声是一个输出阻抗为零的噪声产生器输出的白噪声，通过图示的滤波器后，输出的功率谱密度为

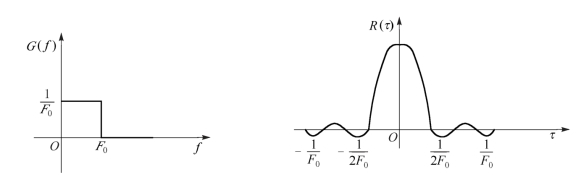
图5-5　输出的噪声功率谱密度及其相关函数

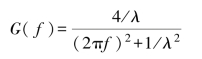
式中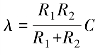，为滤波网络的时间常数。相关函数为

G（f）与R（τ）对应的波形如图5-7所示。从图中可见，相关函数R（τ）随τ增大而单调下降，而不是前两种情况中R（τ）与τ的模糊关系，并且形成此种相关函数的噪声功率谱密度的电路简单。

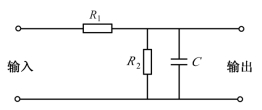
图5-6　低通滤波器

图5-7　白噪声通过低通RC滤波器输出的功率谱密度及其相关函数

四、白噪声通过一个在零点具有最大值的高斯滤波器

白噪声通过以零频为最大值的高斯滤波器输出的功率谱密度为

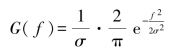
式中，σ为正态分布的均方根。同样通过公式可得相关函数为

R(τ)＝e-2π2σ2τ2

G（f）与R（τ）的图形与图5-7的情况一样，R（τ）也随τ的增长而单调下降，没有模糊情况。但高斯滤波器难以实现。

从以上四种情况可见，第三、第四种情况可得到不模糊的相关函数，但第四种情况要求有较复杂的滤波网络，而第三种情况仅要求阻容网络即可实现。第一、第二种情况存在模糊，给定距带来困难。