差频信号的定距方程

一、锯齿波调频

图3-13所示为锯齿波调频时信号的时间-频率曲线图。图3-13（a）为发射与接收信号的时间-频率曲线，其中实线所示为发射信号频率ft；虚线为回波信号频率fr；载波频率为f0；最大频偏为ΔF；调制信号周期为T。图3-13（b）为某一弹目距离上混频器输出端差频信号ui的时间-频率曲线，其中fi，fi表示这一距离上的差频频率。

由图3-13（a）可求得

从式（3-34）可看出，当调制参数T和ΔF一定时，差频fi与距离R成正比，只要测出fi值就可得到相对应的距离R。

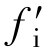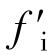在实际调频测距应用中，对差频信号的观测在时间上是随机的，在任何一个观测时刻，尽管探测器与被测物体之间距离是确定的，但因为观测时刻的随机性，使得在观测时刻不知道发射信号和接收信号的频率是多少。尽管此时距离是确定的，电磁波传播时间τ是固定的，但由于观测时刻的随机性，差频可能是fi或。但无论观测时刻如何，在图3-13所示的锯齿波调频中，差频仅是fi或两者中的一个，且fi可能大于，也可能小于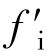。现给出fi、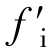与距离的关系曲线如图3-14所示。

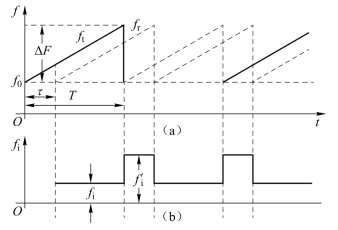
图3-13　锯齿波调频某个距离上的距离差频频率

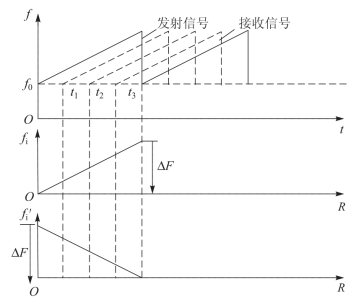
图3-14　距离与差频关系曲线

图3-14中上图为发射信号与接收信号的时间与频率关系的曲线，下两个图为差频与延迟时间（距离）的关系曲线。从图3-14中可见，在任何距离上，由于观测时刻的随机性，锯齿波调频的差频存在两个，一个为fi，另一个为，且

因此，有了fi的表达式，也就有了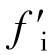的表达式

二、三角波调频

图3-15所示为三角波调频信号的时间-频率曲线图。与上述锯齿波调频相类似，也可求出差频频率。

图3-15　三角波调频时间-频率曲线

或

式（3-38）仅适用于nT＜t＜T/4＋nT（n＝0，1，2，…，N）。

三角波调频与锯齿波调频均为线性调频，但差频与距离的具体关系式不同。

图3-15中，T为调制周期，ft为发射信号频率，fr为接收信号频率，ΔF为调制频偏。从图可见：

（1）在（0～τ）内的任何一个距离上，差频从0到Δf之间变化，距离大（τ越大），Δf大，在τ＝T/4时Δf最大，达到2ΔF，且某个距离上的最大差频Δf可用式（3-37）计算；

（2）在（0～τ）内的任何一个距离上，由于观测时刻的不同，差频0～Δf的各频率出现均不少于两次。

三、正弦波调频(www.xing528.com)

图3-16所示为正弦波调频信号的时间-频率曲线图。发射信号频率为

ft＝f0＋ΔFcosΩt

回波信号频率为

fr＝ft(t-τ)＝f0＋ΔFcosΩ(t-τ)

混频器输出端差频信号频率为

通常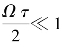，则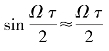

图3-16　正弦波调频时间-频率曲线

由上式可见，差频频率fi是按正弦规律变化的，其最大值为

在调制参数一定的条件下，差频频率最大值fim也是与距离R成正比的。

在正弦波调制时，其差频信号频率是以Ω为角频率按正弦规律变化的。

四、线性调频测距精度

所说的测距精度是指引信能区分的最小距离。式（3-38）给出了三角波调频的距离公式。引信可区分的最小距离可表示为

式（3-41）说明，差频测距的精度取决于调制周期、调制频偏、电路对频率的分辨能力。其中起决定作用的是电路对频率的分辨能力。

五、差频公式的分析

从上述分析，可以得到调频测距的几点重要结论。

（1）差频测距中的差频频率是连续的，差频与距离存在对应关系，因此，可以连续测距。

（2）在锯齿波调频时，差频信号的频率与传播时间（距离）的关系曲线与发射信号的频率与时间关系的曲线变化规律完全相同；由于观测时刻的随机性，同一距离会产生两个差频，两个差频的和为ΔF。

（3）在三角波调频时，差频信号的频率与传播时间（距离）的关系在0＜t＜T/4时段内观测时，是有规律的，可以用式（3-38）表示。

（4）三角波调频存在“差频不规则区”。且由于观测时刻的随机性，同一距离可能对应几个差频频率。

（5）用周期信号调制时，存在测距模糊。

在三种不同调制规律下推导出的差频公式都明确给出了差频信号频率fi与距离R成比例的关系，这些就是差频测距的基本原理。

另外上述分析是在没有考虑系统与目标之间相对运动的条件下进行的，如果考虑引信与目标之间的相对运动，将使差频信号发生变化，从而影响差频公式的精确度。当引信与目标之间具有相对运动时，回波信号相对于发射信号的延迟时间，将是时间的函数，即τ是随时间而变化的。在发射信号的一个调制周期T内，τ将变化2vRT/c。若弹目接近速度vR为1Ma，则在一个调制周期内τ变化为2×10-6T数量级。τ的这种变化对差频频率产生两方面的影响：一方面使发射信号频率相对于反射信号频率的变化不再是确定不变的，而是随时间而变化的；另一方面将使回波产生多普勒频移。这样必将使回波信号及差频信号的时间-频率曲线也发生变化。