多普勒效应原理及应用

多普勒效应的实质是：在振荡源和接收机之间存在相对运动时，接收机所接收到的振荡频率与振荡源的振荡频率不同。这一现象首先在声学上由奥地利物理学家多普勒于1842年发现。

假设声源S以速度vS向静止的接收机R运动（如图2-1（a）），与接收机距离为r的波源在瞬时t1发出的波到达接收机的瞬时为

式中，vW为波的传播速度。

在瞬时t2＝t1＋τ波源发出的波到达接收机的瞬时为

如果波源的振荡频率为f0，则在τ时间内发出的波数为

而接收机接收的频率是

式中，θ＝θ2-θ1。

利用式（2-1）、式（2-2）和式（2-3）求式（2-4）可得

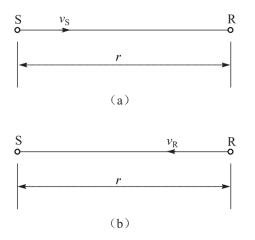
图2-1　声学中的多普勒效应

（a）接收机静止，声源运动时的多普勒效应；（b）接收机运动，声源静止时的多普勒效应

反之，如果振荡源静止而接收机R以速度vR向波源运动（如图2-1（b）），与上面分析类似，可以得到

θ1＝t1＋r/(vW＋vR)

θ2＝t2＋(r-vRτ)/(vW＋vR)

于是

从式（2-5）和式（2-6）中可以看出，当波源和接收机存在相对运动时，接收机接收到的振荡频率与振荡源的振荡频率不同，这就是多普勒效应。

下面看一下电动力学中的情况。把接收机放置在原点为O的坐标系K上，而把发射机放置在原点为O′的坐标系K′上，如图2-2所示。设发射机的坐标系K′相对于接收机的坐标系K沿着x轴以速度v向右运动。发射机的振荡频率是f0，现在确定坐标系K上的接收机接收到的振荡频率为f。

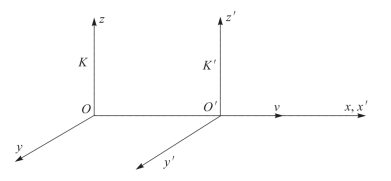
图2-2　电动力学中的多普勒效应

根据爱因斯坦-罗伦兹变换公式，K和K′坐标系上坐标和时间的对应关系为

式中，c为光速。

在发射机发出信号的过程中，在接收机坐标系K上标出两个时间t1和t2及对应的x轴上两点x1和x2，其坐标对应于这些瞬时的波源位置。那么接收机接收信号的持续时间（根据坐标系K上的时钟）等于

(www.xing528.com)

而

x2＝x1＋vτ

因为发射机与接收机之间有相对运动，所以接收机接收信号的起始和终了瞬时θ1和θ2（在坐标系K上测量）将不同于t1和t2，而是

式中，r为瞬时t1发射机和接收机之间的距离。

根据式（2-9），可以计算出在坐标系K上作用于接收机的持续时间θ为

现在求在这个时间内到达接收机的振荡数。

设发射机的振荡频率为f0（在坐标系K′上）。它发射出振荡信号的持续时间在坐标系K′上应该为

式中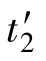，和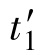为坐标系K′上振荡信号发出的终了和起始时间。根据式（2-7）可得

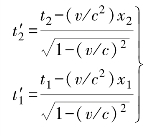
由此得到

根据式（2-12），可求得在时间间隔θ内到达接收机的振荡数

而由接收机接收的频率为

式（2-14）、式（2-5）和式（2-6）都是多普勒效应的表达式，但两式不论从本质上还是形式上完全不同，即传播速度比较小和传播速度接近光速时多普勒效应的表达式是不同的。如果发射机和接收机间相对速度远小于光速，即vc，则式（2-14）完全可以近似地表示成与式（2-6）相同的形式（同时考虑远离和接近的两种情况）

其中负号表示接收机向远离发射机方向运动。由于vW＝f0λ0，λ0为振荡信号波长，故式（2-15）又可写成

式中，v/λ0称为多普勒频率。

在无线电引信系统中，发射机和接收机处于同一弹体中，式（2-16）表示与引信有相对运动的目标处的振荡频率。那么由接收机接收到由目标反射的信号之多普勒频率将增大一倍（用vR代替v），有

令

将fd称为无线电引信的多普勒频率。

如果弹目是逐渐接近的，则fd为正值；如果弹目是逐渐远离的，则fd为负值。