喷射压力条件下燃油的典型物理特性分析

1.简介

这里将比较详细的介绍R.Payri^[16]等人研究的结果，以供高压共轨喷油系统的开发研制者参考。R.Payri等人的工作将燃油物理特性的研究提高到180MPa，温度提高到了343K，并选择了三种燃油进行研究，它们是：一种生物柴油——Rape Methyl Ester（RME）；一种冬天使用的普通柴油（Winter fuel）——Arctic fuel（ARCT）；一种常用的由Repsol公司生产的普通柴油——Elite fuel，并将该柴油作为参照物（Reference fuel），和其他两种燃油进行比较研究。

R.Payri等人在一个专门设计研制的高压环境下测试了三种燃油的声速，用普通的测试设备在大气环境下测试了三种燃油的密度，然后经过适当的数学处理得到了在高压、高温环境下的三种燃油的密度和体积弹性模量。

2.理论基础

因为燃油的等熵声速为

式中 E_s——高压燃油的等熵体积弹性模量；

ρ——燃油的密度；

燃油的等熵体积弹性模量

燃油的等温体积弹性模量

式中 p——燃油的压力。

因为燃油的等熵体积弹性模量E_s和等温体积弹性模量E_T可以用下式连接

式中 α——燃油的等压热膨胀系数；

C_p——比定压热容。

所以从式（9-48）～式（9-51）可以得到

沿着给定的某一条等温线积分上式可以得到联系燃油的声速和密度的关系式

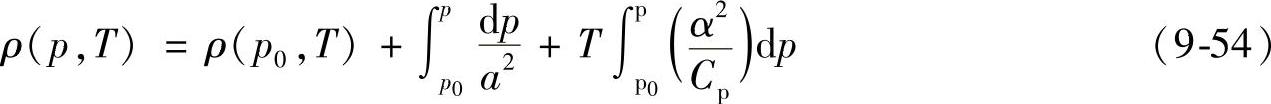
上式中的右边第一项是燃油密度的主要部分，可以直接在大气环境下测得，第二项和声速有关，可以通过沿等温线的积分获得，第三项很小可以忽略不计，因为对于液体，C_p/C_v≈1。

因此求得燃油的声速和密度，利用方程（9-48）既可以求得燃油的体积弹性模量。

3.高压、高温环境下的燃油的声速

通过专门的高压环境下的试验获得的普通柴油（Elitefuel）的声速和压力、温度之间的关系如图9-35所示，通过多项式回归拟合得到相对于每一条等温线的燃油等温声速为

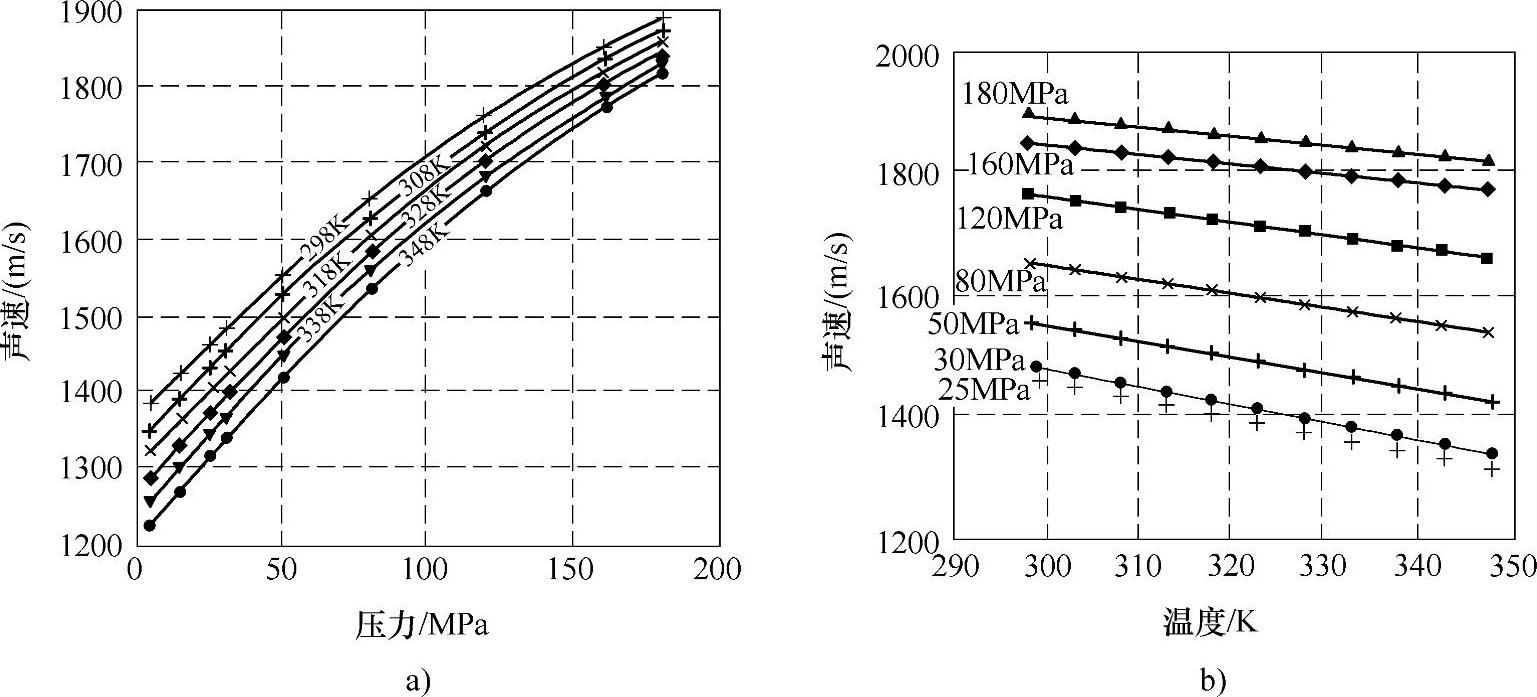
图9-35 普通柴油（Elitefuel）的声速和压力、温度之间的关系

a）在温度分别为298K、308K、318K、328K、338K、348K时，声速和压力的关系 b）在压力分别为25MPa、30MPa、50MPa、80MPa、120MPa、160MPa、180MPa时声速和温度的关系

a=C₁+C₂p+C₃P²+C₃P³ （9-55）

式中的常数C₁，C₂，C₃，C₄可以从表9-3得到，公式（9-54）中，压力的单位是：MPa；声速的单位是：m/s。表9-3中的R²是拟合的公式（9-54）和试验结果的相关性系数，可见相关系数是很高的。表明拟合的公式有比较的精度。表9-2是三种燃油在温度为313K时的基本物理特性。

表9-2 三种燃油在313K时的基本物理特性

表9-3 公式（9-54）中的相关的参数值和相关性系数

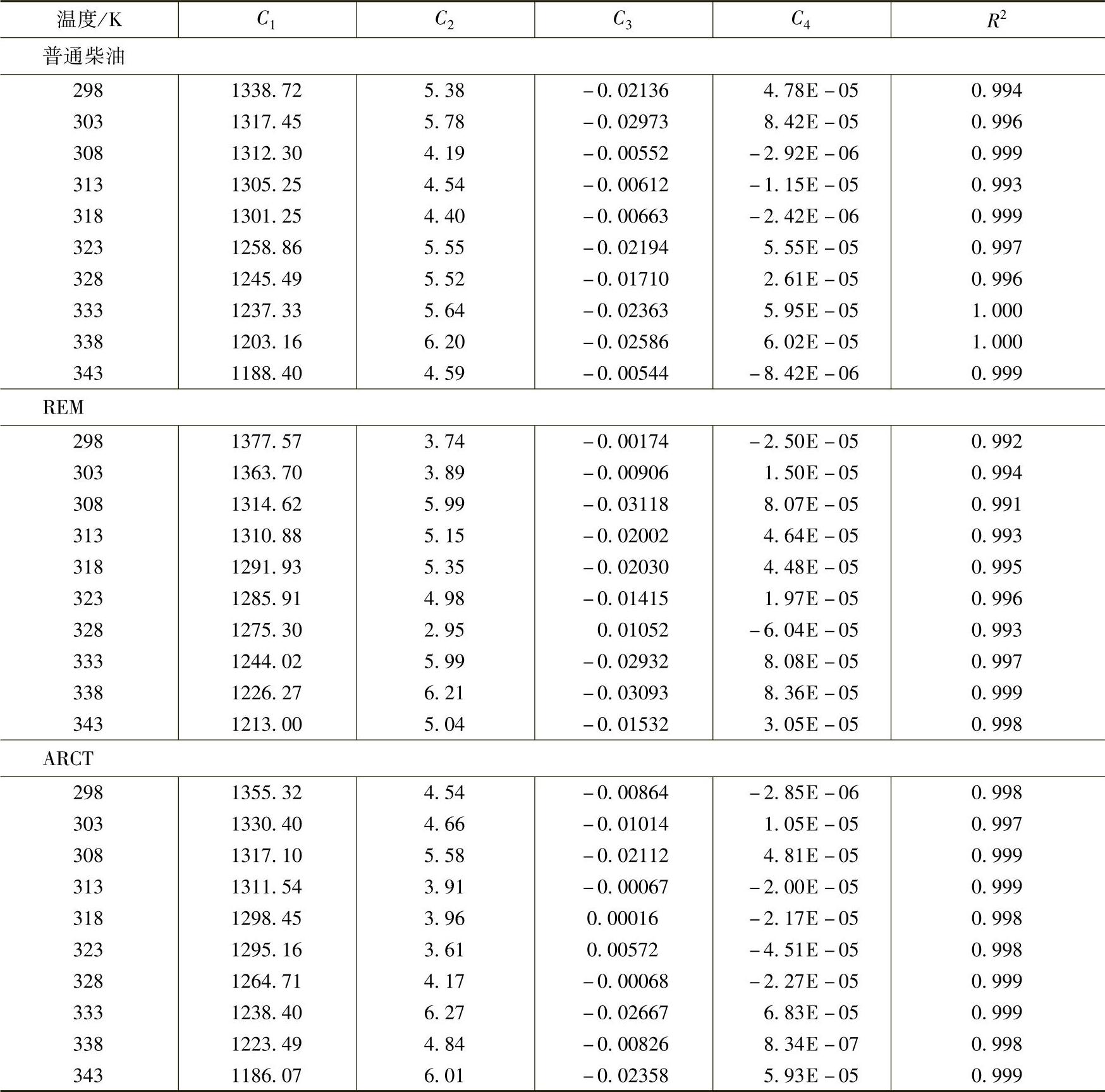
图9-36是三种燃油在给定的压力下，声速和温度之间的关系，图9-37是三种燃油在给定的温度下，声速和压力之间的关系。

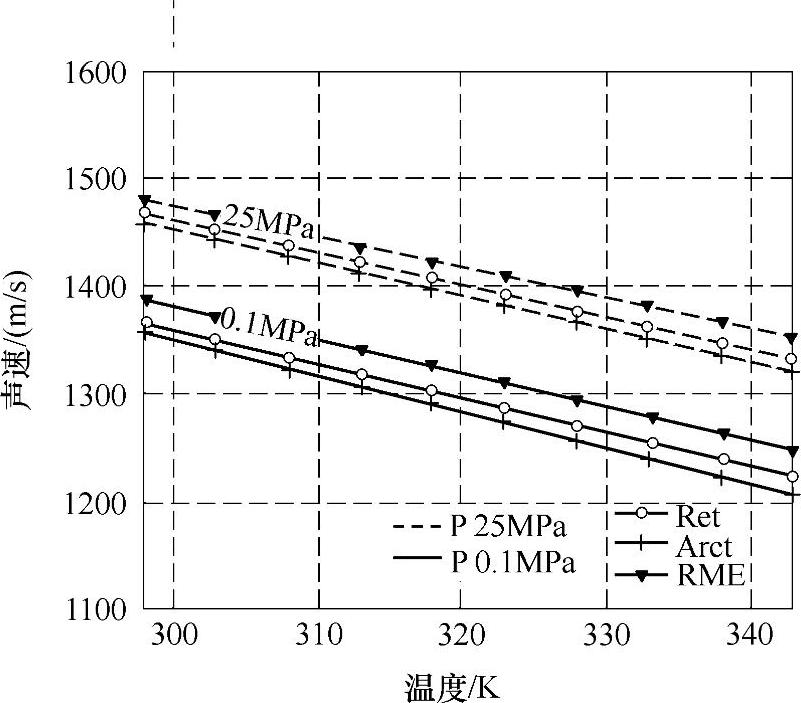
图9-36 三种燃油在给定的压力（0.1MPa、25MPa）下，从方程（9-54）获得的声速和温度之间的关系

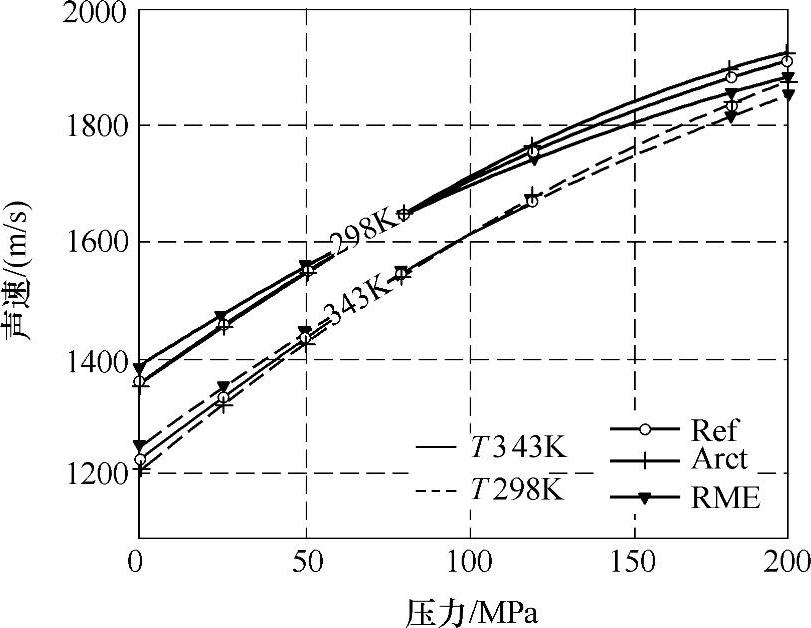
图9-37 三种燃油在给定的温度（298K、343K）下，从方程（9-54）获得的声速和压力之间的关系(www.xing528.com)

综合燃油的声速和压力、温度之间的关系是为

a=k₁+k₂（T-T₀）+k₃（p-p₀）+k₄（p-p₀）2+k₅（p-p₀）·（T-T₀） （9-56）

式中的常数k₁、k₂、k₃、k₄、k₅如表9-4所示。R²为相关性系数。

表9-4 公式（9-55）中相关的参数值和相关性系数

4.高压、高温环境下的燃油的密度

通过在大气压力环境下测试三种燃油的密度，拟合出一个在大气环境压力下的燃油的密度和温度之间的关系

ρ（p₀，T）=C₅+C₆T （9-57）

式中的常数C₅、C₆，如表9-5所示。R²为相关性系数，三种燃油的总的误差不超过0.6%。

表9-5 公式（9-56）中的相关系数和相关性系数

将公式（9-54）代入公式（9-53），并忽略公式（9-53）右边的第三项，可以得到如下的公式

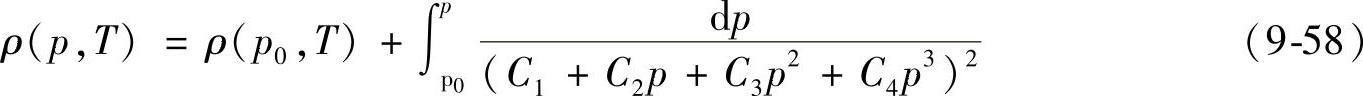
上式中的右边第一项可以利用公式（9-56）确定，这样可以在给定的温度下，计算不同压力时的燃油密度。图9-38是普通柴油（Elitefuel），在不同温度时，燃油的密度随压力变化的曲线。从图9-38中可以看出，该普通柴油的密度随着燃油压力的增大而增大，随着温度增大而减小。图9-39反映了两种不同的温度条件下，三种燃油的密度随压力的变化规律。图9-40两种不同的反映了两种不同的压力下，三种燃油的密度随温度的变化规律。

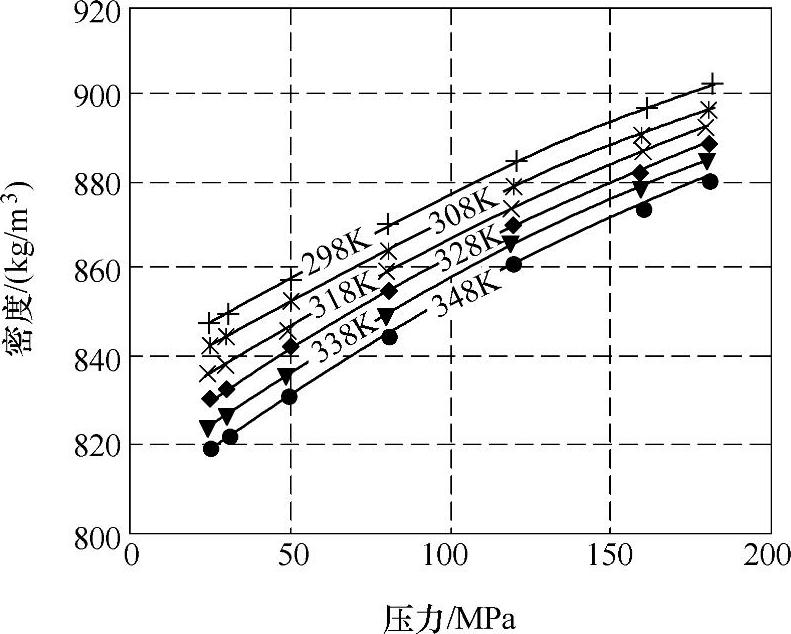
图9-38 普通柴油（Elitefuel）在不同温度（298K、308K、318K、328K、338K、348K）时燃油的密度随压力变化的曲线

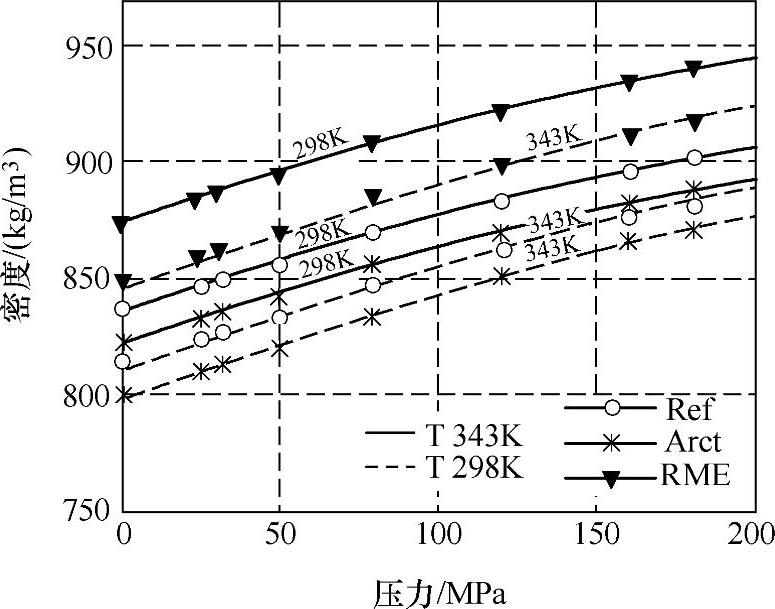
图9-39 两种不同的温度（298K、343K）条件下，从方程（9-57）获得的三种燃油的密度随压力的变化规律

综合考虑燃油的密度和压力、温度之间的关系的表达式为

ρ=k₁+k₂（T-T₀）+k₃（p-p₀）+k₄（p-p₀）2+k₅（T-T₀）2+k₆（p-p₀）（T-T₀） （9-59）

式中的常数k₁、k₂、k₃、k₄、k₅、k₆的数值可以查表9-6。

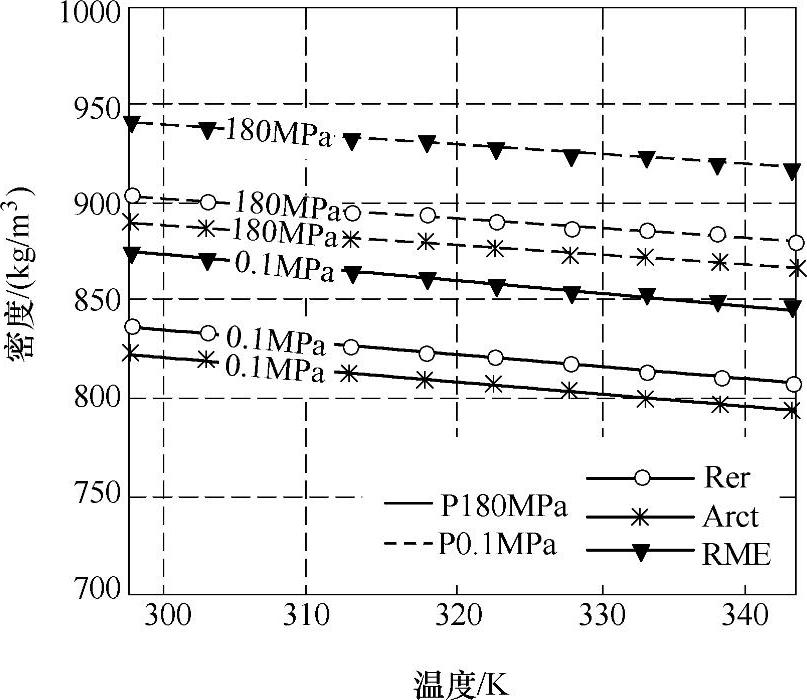
图9-40 两种不同的压力（180MPa、0.1MPa）下，从方程（9-57）获得的三种燃油的密度随温度的变化规律

表9-6 公式（9-58）中的相关系数和相关性系数值

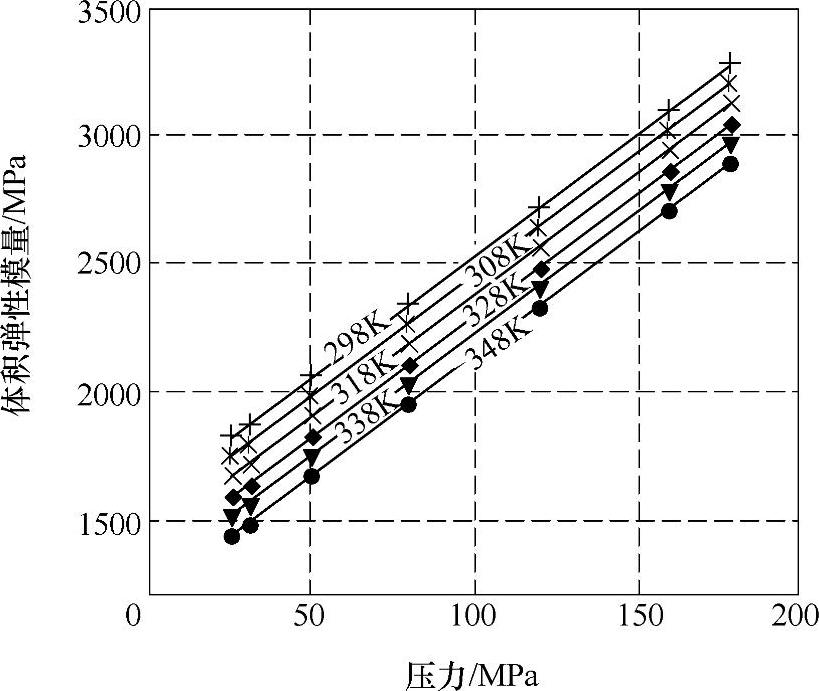
图9-41 普通柴油（Elitefuel）在不同温度（298K、308K、318K、328K、338K、348K）时的体积弹性模量随压力变化的曲线

5.高压、高温环境下的燃油的体积弹性模量

利用得到的燃油的声速和密度，应用公式（9-48）就可以求得在高压、高温环境下的燃油的体积弹性模量。图9-41是普通柴油（Elitefuel），在不同温度时，燃油的体积弹性模量随压力变化的曲线。可以看出，在给定的温度下，普通柴油（Elitefuel）的体积弹性模量随压力的变化几乎是线性的，而且随压力的增大而增大，增长的幅度也比较大。图9-42是三种燃油在给定的温度条件下的体积弹性模量随压力变化的曲线，可以看出，该曲线几乎是直线，说明线性度很好，同样也是随着压力的增大而增大。而图9-43则是在给定的压力下，三种燃油的体积弹性模量随温度的变化规律。可以看出，此时随着温度的增大，燃油的体积弹性模量下降。

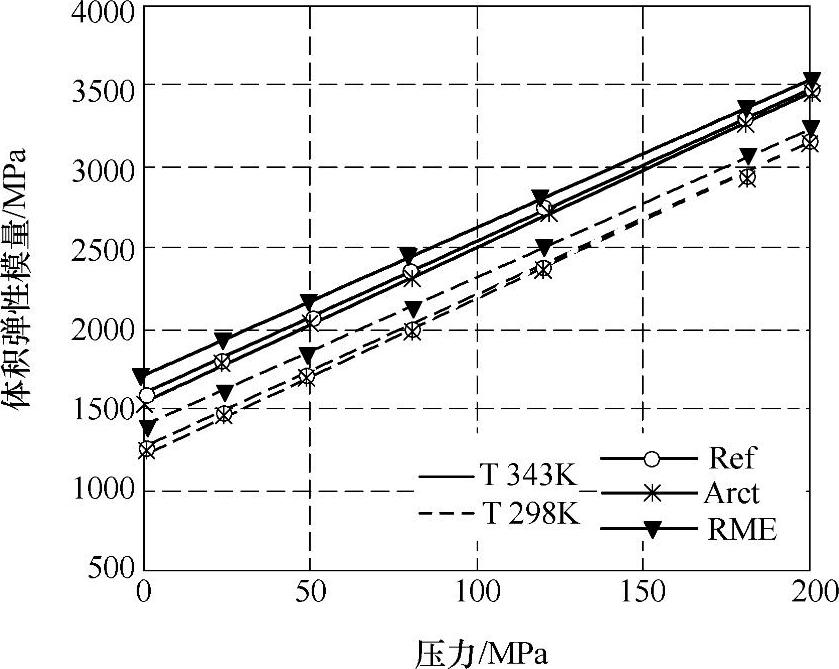
图9-42 三种燃油在给定温度（298K、343K）条件下的体积弹性模量随压力变化曲线

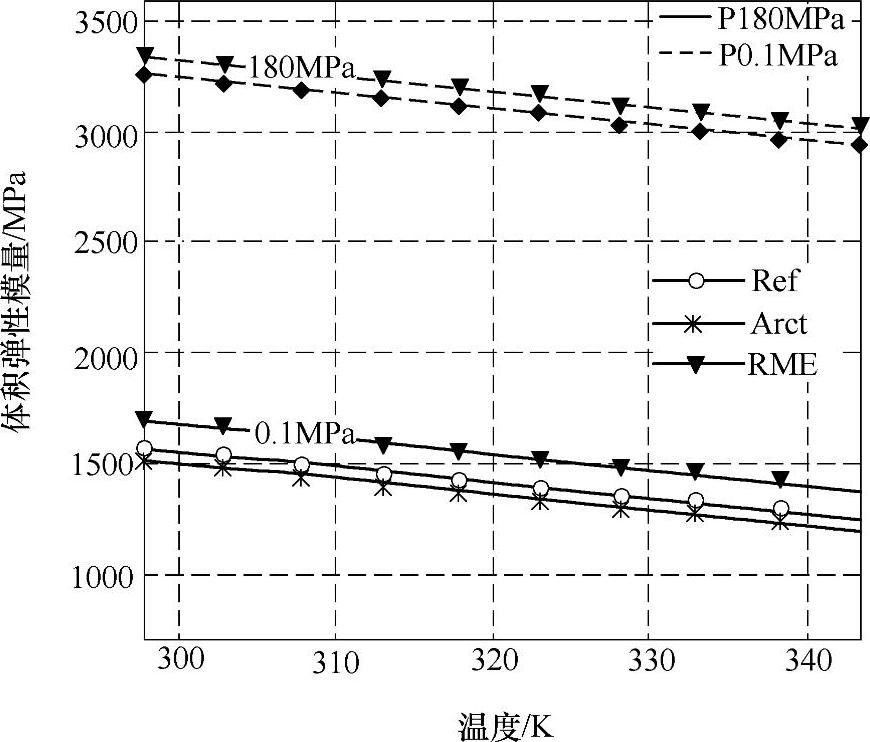
图9-43 三种燃油在给的压力（180MPa、0.1MPa）下三种燃油的体积弹性模量随温度的变化规律

综合考虑燃油的体积弹性模量和压力、温度之间的关系的表达式为

E=k₁+k₂（T-T₀）+k₃（p-p₀） （9-60）

式中的常数k₁、k₂、k₃的数值可以查表9-7。

表9-7 公式（9-59）中的相关系数和相关性系数值