热流体动力学模型的优化：特点与应用

整个喷油系统的液压系统基本都是由各种空腔或容腔所组成的，这些空腔之间通过相应的管道或油道连接。因此各种空腔可以按照相同的维数问题来处理，而各种油管可以按一维问题处理。按照集总质量模型，各种空腔中的燃油压力和温度不随空间位置变化，仅随时间变化。而在高压油管中，燃油的压力和温度可以沿着油管的轴线和时间变化。

高压油泵的输出口的随时间变化的燃油的压力和温度作为该模型的输入变量，这样可以将高压油泵泵油时压缩燃油产生的油液的热流体动力学效应和压力的调节作用反映出来。共轨管是一个管状元件，它可以按一组空腔处理，每一个空腔有相应的高压油管与其连接。

喷油器的高压油入口处安装的缝隙式滤油器处理为液阻元件，而此液阻元件的上、下游，即出入口，按空腔处理。喷油器的最关键的特征是控制柱塞上端的控制腔，该控制腔有一个进油阻尼孔和一个出油阻尼孔。

1.一维非定常可压缩正压流体运动的支配方程

高压油管中的一维非定常可压缩正压流体运动的支配方程可以从其相应的连续性方程和动量方程推出

式中 t——时间变量；

x——沿高压油管轴线的空间变量；

ρ——垂直于管道轴线截面的平均燃油密度；

p——垂直于管道轴线截面的平均压力；

u——垂直于管道轴线截面的平均流速；

d——管道的内径。

由于在高压共轨喷油系统的高压油管中始终存在压力波动以及水锤现象，而且压力波动频率比较高，因此公式（9-2）中描述油液和管壁内表面的剪应力τ_w的公式为

式（9-3）中，左边第一项表示剪应力τ_w稳态部分，其中的f为Darcy-Weisbach摩擦系数。第二项则表示与压力波动频率相关的瞬态剪应力，这是一个卷积积分，其中的权函数w（t-λ）

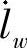——单位质量流体功率粘性耗散。

将动量方程的两边乘以u，并结合连续性方程可以得到如下的方程

式中 ν——油液的运动粘度；

Re——雷诺数；

δ——在层流条件下为1。

对于纯液体的等温管道流动或热力学管道流动（也就是说油液的温度保持不变或油液的温度仅仅和压力或者密度有关），一维非定常可压缩正压流体运动的支配方程除了上述的连续性方程和动量方程之外，只需要再补充一个的油液的状态方程即可，因为是正压流体，所以该状态方程为

p=p（ρ）

但是因为要研究的问题是热流体动力学问题，也就是说要考虑燃油在高压或超高压环境下的压缩升温，所以能量方程是必须要考虑的。一维非定常可压缩正压流体运动的能量方程为

式中 h₀——单位质量流体的总焓，h₀=h+u²/2；

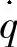——单位质量流体通过边界（即通过高压油管管壁）交换的热量；

利用从此方程，化简能量方程（9-4），可以得到，所谓的“热方程”

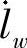——单位质量流体功率粘性耗散。

将动量方程的两边乘以u，并结合连续性方程可以得到如下的方程

利用从此方程，化简能量方程（9-4），可以得到，所谓的“热方程”

式（9-6）中引进熵的概念，就可以得到式（9-7）所表示的适应各种基本热力过程的流体状态变量之间的热力学关系式

式（9-6）中引进熵的概念，就可以得到式（9-7）所表示的适应各种基本热力过程的流体状态变量之间的热力学关系式

式中 T——流体的当地温度；

s——单位质量流体的熵。

考虑高压燃油在高压油管中流动时，通过油管管壁的热交换和油管内的能量的粘性耗散，假设油管内的流动过程是多变（多方）过程，从式（9-7）可以得到如下的流体状态变量之间的热力学关系式

式中 T——流体的当地温度；

s——单位质量流体的熵。

考虑高压燃油在高压油管中流动时，通过油管管壁的热交换和油管内的能量的粘性耗散，假设油管内的流动过程是多变（多方）过程，从式（9-7）可以得到如下的流体状态变量之间的热力学关系式

式中 c——多变（多方）过程的比热容。

对于纯液体，焓的微分形式的表达式为

式中 c——多变（多方）过程的比热容。

对于纯液体，焓的微分形式的表达式为

这样从式（9-8）、式（9-9），并考虑液体在温度为T时的声速

这样从式（9-8）、式（9-9），并考虑液体在温度为T时的声速

可以得到联系燃油压力和温度的方程

可以得到联系燃油压力和温度的方程

方程（9-10）和纯液体的状态方程用来封闭方程（9-1），而纯液体的状态方程为

p=p（ρ，T）

所以

方程（9-10）和纯液体的状态方程用来封闭方程（9-1），而纯液体的状态方程为

p=p（ρ，T）

所以

因为是正压流体

因为是正压流体

所以可以得到纯液体的状态方程为

所以可以得到纯液体的状态方程为

式中 β——液体的体积热膨胀系数。

式中 β——液体的体积热膨胀系数。

式中 E_T——液体的等温体积弹性模量。

式中 E_T——液体的等温体积弹性模量。

因为存在两个互相独立的联系油液的压力、温度、密度的热力学关系式，因此，这种油液系统应该是单变量的系统，也就是说，只需要一个精确的热力学关系式来描述油液内部的状态。因此，为了获得多方过程油液压力波的传播速度，计算方程（9-1）中的压力梯度

因为存在两个互相独立的联系油液的压力、温度、密度的热力学关系式，因此，这种油液系统应该是单变量的系统，也就是说，只需要一个精确的热力学关系式来描述油液内部的状态。因此，为了获得多方过程油液压力波的传播速度，计算方程（9-1）中的压力梯度

然后重写方程（9-1）

然后重写方程（9-1）

式中 A——方程（9-15）的Jacobian矩阵。

式中 A——方程（9-15）的Jacobian矩阵。

该矩阵的特征值就是高压油管中的压力波的传播速度表达式

该矩阵的特征值就是高压油管中的压力波的传播速度表达式

所以高压油管中油液的声速为

所以高压油管中油液的声速为

如果高压油管中油液按多方过程处理，则可以得到声速的具体表达式

如果高压油管中油液按多方过程处理，则可以得到声速的具体表达式

此公式的推导过程如下。

将方程（9-8）代入方程（9-9），可以得到

此公式的推导过程如下。

将方程（9-8）代入方程（9-9），可以得到

该式重写

该式重写

从方程（9-11）可以得到(www.xing528.com)

从方程（9-11）可以得到

考虑到

a²=dp/dρ 和 a²_T=E_T/ρ

从上式可以得到

考虑到

a²=dp/dρ 和 a²_T=E_T/ρ

从上式可以得到

从方程（a2）和（a4）可以得到

从方程（a2）和（a4）可以得到

这样可以得到

这样可以得到

因为比定容热容为

因为比定容热容为

又因为内能

e=h-pv

所以从方程（9-9）和（a7）得到

又因为内能

e=h-pv

所以从方程（9-9）和（a7）得到

另一方面，对于等容过程，方程（9-11）可以变成

另一方面，对于等容过程，方程（9-11）可以变成

将此式代入（a8）式得到

将此式代入（a8）式得到

最后结合方程（a10）和（a6）得到

最后结合方程（a10）和（a6）得到

此即（9-19）式。

2.液压容腔的热力学方程

对于所研究的高压共轨喷油系统中的各种液压容腔都可以用下面的质量守恒方程描述

此即（9-19）式。

2.液压容腔的热力学方程

对于所研究的高压共轨喷油系统中的各种液压容腔都可以用下面的质量守恒方程描述

式中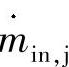——进入液压容腔j的质量流量；

式中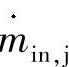——进入液压容腔j的质量流量；

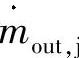——流出液压容腔j的质量流量；

V_j——液压容腔j的体积；

ρ_j——液压容腔j内油液的密度。

如果该液压容腔j和一个高压油管连接，则通过求解描述该高压油管偏微分方程，所求的解，即可作为液压容腔j和该高压油管的边界条件。如果两个液压容腔j和j+1通过一个液阻相连接，则通过该液阻的体积流量可以用下式描述

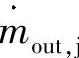——流出液压容腔j的质量流量；

V_j——液压容腔j的体积；

ρ_j——液压容腔j内油液的密度。

如果该液压容腔j和一个高压油管连接，则通过求解描述该高压油管偏微分方程，所求的解，即可作为液压容腔j和该高压油管的边界条件。如果两个液压容腔j和j+1通过一个液阻相连接，则通过该液阻的体积流量可以用下式描述

式中 Δp=p_j-p_j+1；

A——液阻的流通截面积；

式中 Δp=p_j-p_j+1；

A——液阻的流通截面积；

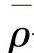——经过液阻的流动按照等焓过程处理时，油液的平均密度。

当高压燃油经过液阻时，燃油的温度会增加，此时的燃油温度的增加的大小可以运用方程（9-9）来计算，此时按等焓过程处理，即dh=0。

公式（9-21）中的燃油的流量系数μ要根据具体情况具体处理。燃油经过针阀和针阀座的形成的液阻时，要按非稳定流量系数处理^[7]、[8]，其他情况要根据燃油的雷诺数确定

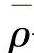——经过液阻的流动按照等焓过程处理时，油液的平均密度。

当高压燃油经过液阻时，燃油的温度会增加，此时的燃油温度的增加的大小可以运用方程（9-9）来计算，此时按等焓过程处理，即dh=0。

公式（9-21）中的燃油的流量系数μ要根据具体情况具体处理。燃油经过针阀和针阀座的形成的液阻时，要按非稳定流量系数处理^[7]、[8]，其他情况要根据燃油的雷诺数确定

式中 Re——燃油流经液阻时的雷诺数数；

Re_ct——燃油的临界雷诺数数；

μ_max——燃油流经液阻时流态为充分发展的湍流时的流量系数。

公式（9-22）中的双曲正切函数tanh，表示当燃油的燃油的雷诺数，Re>>Re_ct时，流量系数μ可以按常数处理，相反，当Re<<Re_ct时，流量系数μ是雷诺数的线性函数。

燃油的临界雷诺数数Re_ct的取值范围为：1000～150，1000对应简单的液阻几何形状，

150对应复杂的液阻的几何形状。μ_max也取决于液阻的几何形状，同时也和流经液阻的收缩断面时燃油的特性有关，因为在最小收缩断面处会产生气穴^[9]。

因为在各种液压容腔j内可以认为燃油的运动速度为零，所以可以不考虑动量定理，只需要再增加能量方程和流体的状态方程就可以组成完备的描述液压容腔j的数学模型。

式中 Re——燃油流经液阻时的雷诺数数；

Re_ct——燃油的临界雷诺数数；

μ_max——燃油流经液阻时流态为充分发展的湍流时的流量系数。

公式（9-22）中的双曲正切函数tanh，表示当燃油的燃油的雷诺数，Re>>Re_ct时，流量系数μ可以按常数处理，相反，当Re<<Re_ct时，流量系数μ是雷诺数的线性函数。

燃油的临界雷诺数数Re_ct的取值范围为：1000～150，1000对应简单的液阻几何形状，

150对应复杂的液阻的几何形状。μ_max也取决于液阻的几何形状，同时也和流经液阻的收缩断面时燃油的特性有关，因为在最小收缩断面处会产生气穴^[9]。

因为在各种液压容腔j内可以认为燃油的运动速度为零，所以可以不考虑动量定理，只需要再增加能量方程和流体的状态方程就可以组成完备的描述液压容腔j的数学模型。

式中 p_j，T_j，e_j——分别液压容腔j内的燃油的平均压力、温度和内能；

h_j——液压容腔j内单位质量流体的焓；

h_0in，j——液压容腔j内单位质量流体的总焓；

c_ch——比热容，该比热容考虑了通过液压容腔j的壁面的热交换和能量耗散，这是一个模型拟合的参数^[10]。

式中 p_j，T_j，e_j——分别液压容腔j内的燃油的平均压力、温度和内能；

h_j——液压容腔j内单位质量流体的焓；

h_0in，j——液压容腔j内单位质量流体的总焓；

c_ch——比热容，该比热容考虑了通过液压容腔j的壁面的热交换和能量耗散，这是一个模型拟合的参数^[10]。