高压共轨喷油系统仿真建模及解算方法

由于需要仿真模拟计算的零部件和系统的多种多样，因此，针对不同的求解问题可以采用不同的仿真模拟方法。例如，高压油泵内部流场的模拟计算一般采用计算流体力学方法进行仿真，喷油器的动态特性的模拟要采用微分方程求解方法进行分析。高压油管的动态特性的分析采用计算流体力学和微分方程求解方法相结合的方法进行分析。

1.计算流体力学方法

流体力学分析方法是高压共轨喷油系统仿真分析的基础，而流体力学问题也是高压共轨喷油系统中最难以精确求解的问题。计算流体力学数值求解方法有很多种，主要用于二维、三维空间域上的偏微分方程的求解，以分析复杂流场的压力、速度等参数的分布特征。由于求解的方法的计算工作量大，耗费机时多，因此过去一般只适用于求解静态流场分布特征问题，现在由于计算机运算速度的提高，该方法也广泛用于求解动态流场问题。

虽然各种计算流体力学求解方法的数学原理各不相同，但是所有方法的共同点是离散化和代数化。总体来说，计算流体力学求解方法的基本思想是：将原有连续的求解区域划分为网格或单元子区域，在其中设置有限个离散点（称为节点），将求解区域中的连续函数离散为这些节点上函数值；通过某种数学原理，将作为控制方程的偏微分方程转化为联系节点上待求函数值之间关系的代数方程（离散方程），求解所建立起来的代数方程获得求解函数的节点值。

各种计算流体力学数值方法的主要区别在于求解区域的离散方式和控制方程的离散方式的不同。在流体力学数值方法中，应用比较广泛的是有限差分法，有限元法，边界元法，有限体积法。

2.微分方程求解方法

通常时间域上的微分方程是用于描述高压共轨喷油系统中的零部件或整个系统的动态特性的数学模型，其求解方法有时域法和频域法。一般为了评价喷油器、电液比例溢流阀等部件的响应特性，多采用时域法进行分析；为了分析电液比例溢流阀、电液比例节流阀的稳定性或控制精度，多采用频域法进行分析。

从求解系统的数学模型来看，时域法是对系统的微分方程不做任何变换，直接在时间域中求解的方法，用时域法进行分析，所得元件或系统的响应特性是时间的函数，用系统对阶跃、斜坡等信号的响应曲线表示。从这些曲线中可以得到系统的响应时间、超调量以及稳态误差等信息。(www.xing528.com)

频域法是通过傅里叶变换将微分方程变换成频率域中的代数方程进行求解，所求的元件或系统的响应特性是频率的函数，通常以伯德图（Bode）或奈奎斯特（Nyquist）曲线的形式表示。伯德图表示的是系统的幅值和相角随频率变化的关系，分别称为幅频特性和相频特性。从伯德图可以得到系统的稳定性、幅值余量和相角余量等参数。

3.键合图法

键合图（BondGraph）又称为键图，是20世纪60年代美国麻省理工学院HenryM.Paynter教授提出的一种系统建模方法，主要用于建立机械、电气、液压等系统的动态数学模型，以便于分析整个系统的动态特性。所谓键合图（BondGraph），简单地说就是将所研究的动力系统内部功率的产生、传递、转换和损耗，用功率键和若干作用元以及相关的连结符号，按一定的规律连结起来用于描述动态系统的一种图形。键合图类似于控制理论中的框图或信号流图。传递函数框图、信号流图、键合图以及微分方程都能描述动态系统，但与传递函数框图、信号流图相比，键合图更接近于实际物理系统。例如图9-1a所示的锥阀，其数学模型可以用图9-1b所示的键合图来描述。

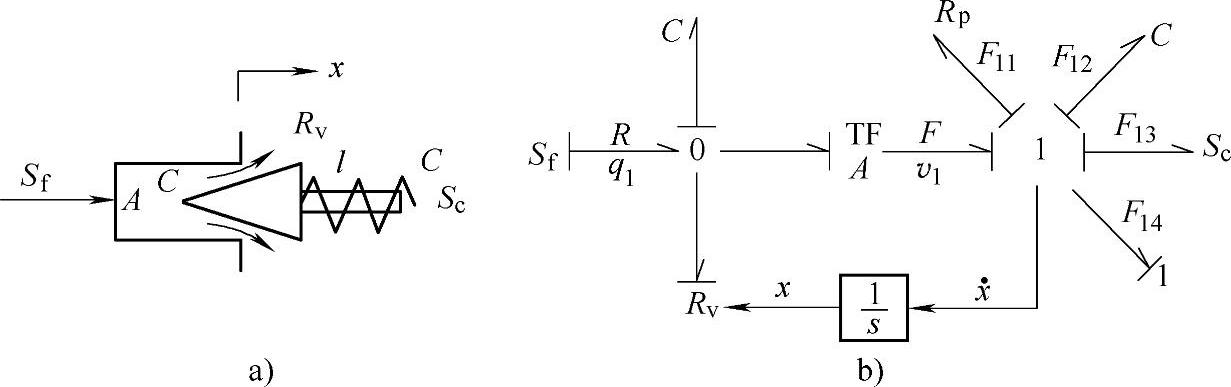
图9-1 典型的圆锥阀及其功率键合图

由于键合图是以能量守恒原理为基础，因此它能更清楚、更直观的表达系统的能量特性、物理效应和系统的内在联系，根据键合图，可以很方便地判断出状态方程的阶次，并建立状态方程，可以根据需要取舍或改变有关系统的参数，进而找出系统的最佳参数及相关准则，实现对系统性能的动态分析。特别是对于具有不同种类能量耦合的复杂系统，如机、电、液耦合系统，键合图是建模的最有力工具。此外，键合图还具有独特的符号推理功能。目前，键合图理论已经在很多科学和工程技术领域得到了广泛的应用，特别是在分析机、电、液耦合系统时，应用键合图理论更加方便。