高速电磁开关阀的开关性能优化分析

1.电磁铁的吸合过程与吸合时间

不论何种方式的电磁铁作为高速开关阀的驱动机构，电磁铁总是一个带铁心的线圈，具有一定的电感值。当加上电压U后，线圈中的电流不能跃变到稳定的I_W（I_W=U/R，R为线圈回路内的电阻值），而是随时间按一定的规律上升，如图6-23所示。当线圈电流增长到I_cd所需时间t_c′_d称为吸合触动时间。当线圈电流增长到I_cd后，电磁铁吸力F_d将大于电磁铁所受反力，衔铁开始运动。衔铁开始运动到最后达到闭合位置所需的时间t_y′_d，称之为吸合运动时间。所以电磁铁的固有吸合时间t_xh包括两部分，即

t_xh=t_c′_d+t_y′_d（6-49）

式中 t_c′_d——吸合触动时间；

t_y′_d——吸合运动时间。

（1）吸合触动时间t_c′_d 当线圈加上直流电压U以后，其电流（或磁通）增长的过渡过程可以由电压平衡方程求得，即

式中 U——线圈电压（V）；

i——线圈电流（A）；

R——线圈回路总电阻（Ω）；

Ψ——线圈总的磁链（Wb）；

t——通电时间（s）。

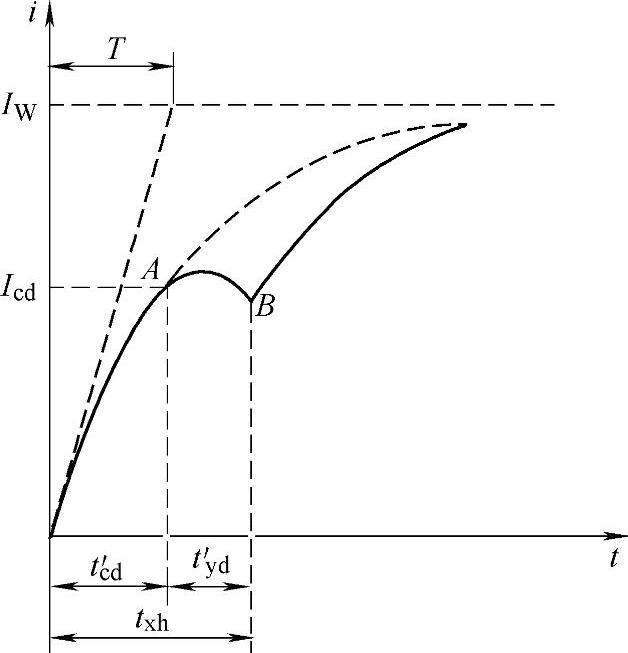
图6-23 线圈电流增长曲线

如果已经由磁路计算求得电磁铁在打开（未吸合）位置δ_k时的励磁特性Ψ=f（i），如图6_-24a所示，则可用图解积分法求得t_c′_d，因为由式（6-50）得

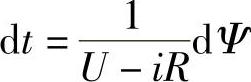
所以

式中 Ψ_cd——触动电流I_cd时的线圈磁链。

图6-24 用图解积分法求t_c′d

a）δ=δ_k时的励磁特性Ψ=f（i） b）由Ψ=f（i）求得的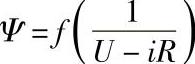

若由Ψ=f（i）逐点计算Ψ=f（1/（U-iR）），如图6-24b所示，则t_c′_d即正比于阴影面积Q。当衔铁处于打开位置时，并且电流又不是很大时，磁路一般并不饱和，则可以认为线圈电感L（L=Ψ/i）为常数，则式（6-50）可以写为

式（6-52）的解为

式中 I_W——线圈的稳态电流值（A），I_W=U/R；

T——线圈的时间常数（s），T=L/R。

可见，电流按指数曲线上升，如图6-23。如果线圈电流达到I_cd后衔铁仍保持不动，则电流将按图中虚线（指数曲线）上升到稳态值I_W。线圈电流到达I_cd所需的时间t_c′_d（单位为s），可令i=I_cd代入式（6-53）求得，即

若令

式中 K_cb——储备常数。

则代入上式得

以上推导并未考虑涡流的影响。实际上，当Φ变化时，导磁体内将会产生环绕磁通的感应电流，即所谓涡流。涡流的作用总是使磁通的变化落后于线圈电流的变化，因此使触动时间变大。在打开位置时，涡流的影响一般不大，可以用一个系数α来考虑它的影响，即

一般α等于1.1～1.3。

为说明涡流的影响，现分析下面的问题：

如果电磁铁有两个线圈，其中一个是励磁线圈，匝数为N₁，另一个是短接线圈，其匝数为N₂，如图6-25所示。

假定磁路为线性，在触动时间内衔铁又静止，故L₁、L₂均为常数，并假定二线圈耦合，即在N₁、N₂中通过同一磁通，于是可列方程

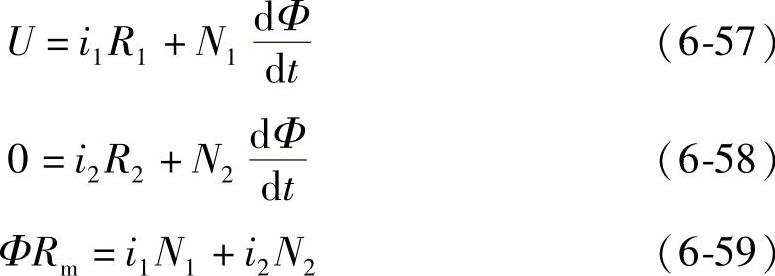
式中 R_m——磁路总磁阻。

由式（6-57）、式（6-58）得

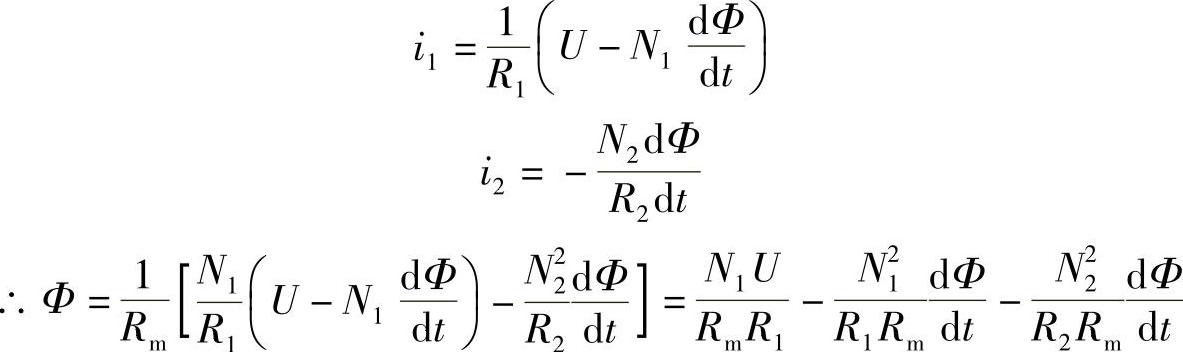
图6-25 双线圈电磁铁

整理后，得

令

其解为

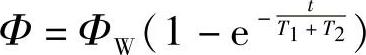
或

当

i=I_cd时，t=t_c′d

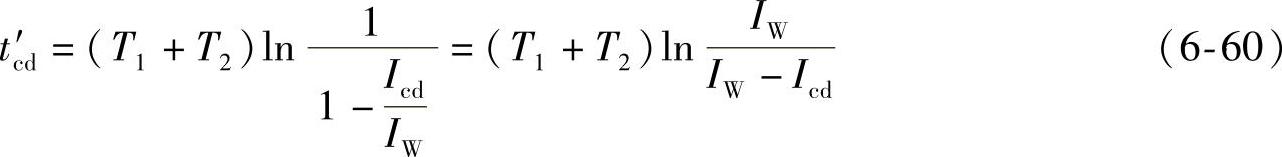
由此可见，短路线圈的存在，使触动时间增长。

励磁线圈的时间常数T₁为

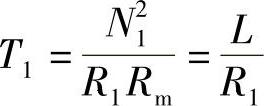
短接线圈的时间常数T₂为

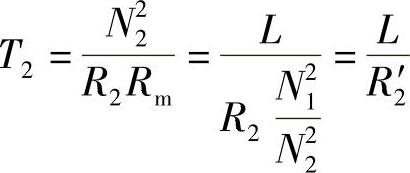
式中 R₂′——归化到励磁线圈的短接线圈电阻。

式（6-60）可写成

现在可利用式（6-61）的结论，考虑涡流对触动时间的影响。如果用绕在静铁心上的一匝短接线圈来等效地代替涡流效应，求出归化到励磁线圈的等效电阻，即可求出计入涡流影响的触动时间t_c′_d。

设铁心截面是圆形，如图6-26所示，涡流在沿着以截面中心为圆心而半径不同的圆周内流动。

在离圆心为r处，取一圆环dr，其所链连的磁通为

Φ_r=Bπr²

环中的感应电动势为

圆环的电导为

圆环涡流损耗为

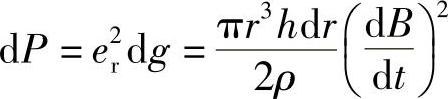
总的涡流损耗为

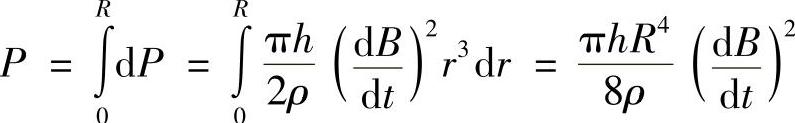
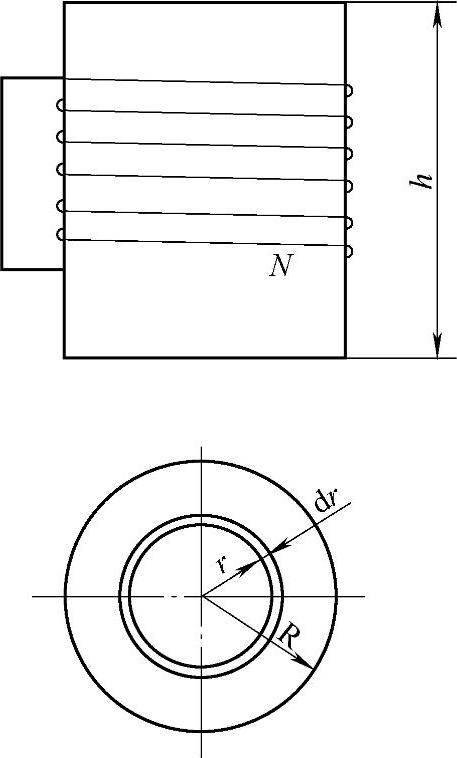
图6-26 铁心的等值电阻

假想铁心外有一短接线圈，匝数为1，电阻为R_wl，线圈中感应电动势为

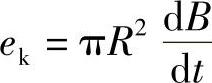
则线圈消耗的功率为

令P=P′，得

归化到励磁线圈的涡流等效电阻为

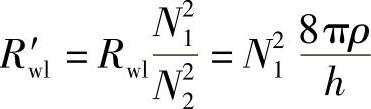
显然涡流的作用也使触动时间增加，则

（2）吸合运动时间t_y′_d 衔铁运动后，电流不再按式（6-53）的指数曲线上升。因为衔铁运动过程中，气隙减小，磁通增大，而磁通的变化将在线圈内感应而产生一个反电动势。这个反电动势和线圈的自感电动势共同阻止线圈电流的增长。此时，由于线圈电感在变化，电路的电压平衡方程将不同于式（6-52）而是

等式右边的第二项为自感电动势，而第三项即为电感变化时的反电动势。因此，电流的增长规律将低于式（6-53）的指数曲线，并且，随着衔铁运动速度的增加，反电动势就愈大，两者的差别就愈大，电流甚至不再上升反而下降，如图6-23中AB段。B点的位置与衔铁运动的速度有关，速度愈大，B点就愈低，到达B点，衔铁已闭合，气隙不再变化，线圈电流又近似地按指数规律增长，不过这时线圈的时间常数已不同于衔铁打开时的电时间常数，因为电感变大了。

电磁铁的运动时间的计算是比较麻烦的，因为衔铁在运动过程中除线圈电感变化外，作用于衔铁上的反作用力和电磁吸力都在变化。计算电流的变化规律以及衔铁的运动时间不仅要研究电和磁的变化规律，还要同时研究衔铁的运动规律，也就是说，必须联立求解下列两个微分方程(www.xing528.com)

电路方程

运动方程

式中 m——衔铁及其他运动部分的质量；

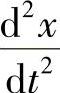——衔铁的运动加速度，x为衔铁的行程；

F_d——电磁铁的电磁力；

F_f——电磁铁的反力。

由于Ψ和F_d是x和i的函数，并且是非线性的关系，F_f也与x与dx/dt有关。因此要用解析法求解以上方程比较困难。为求得简明而又有一定指导意义的结果，设阀芯行程较小，可近似地把电磁铁吸力F_d及运动阻力F_f（即反力，由弹簧力、运动阻力、液动力组成）近似不变，力平衡方程写成

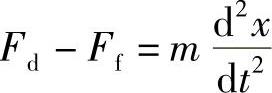
求解得

求解过程如下

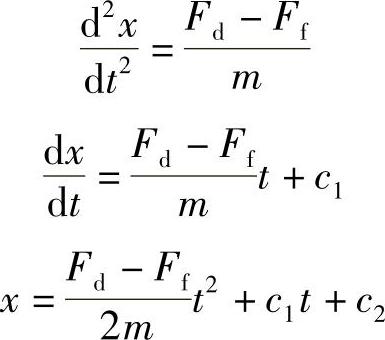
式中 c₁、c₂——积分常数，由初始条件确定。

当t=0时

当x=0，c₁=0，c₂=0

所以

当x=x_d，t=t_y′_d则

2.电磁铁的释放过程和释放时间

从线圈断开电源的瞬间到衔铁开始运动的时间，这段时间为释放触动时间t″_cd，而从衔铁开始运动到恢复到原来打开位置所需时间为释放运动时间t″_yd，电磁铁的固有释放时间t″_sf由以上两个阶段组成，即

t″_sf=t″_cd+t″_yd （6-66）

（1）释放触动时间t″_cd 当电磁铁线圈断电时，如果不计断电时电弧熄灭所需的时间，则可以认为线圈电流瞬间即减到零，此时如果不计涡流的作用，线圈本身也没有短路匝，则可以认为磁通也瞬间降为剩磁值（一般很小），因此t″_cd这段时间也就不存在了。而实际上，由于涡流的影响，磁通不会瞬间由闭合时的稳态磁通Φ_b降到剩磁值Φ_r，而是近似于指数曲线逐渐下降，如图6-27所示。当磁通下降到释放磁通Φ_sf，吸力已不足吸住衔铁而被释放，这段时间即为释放触动时间t″_cd。因此描述此段过程的电路方程和电磁铁的受力方程为， F_d≥F_f

求解得

但若考虑线性磁路

当t=0时，i=I_W=U/R，则上式的解为

当i=I_q时，t=t″_cd，则释放触动时间为

再计入涡流的影响，则

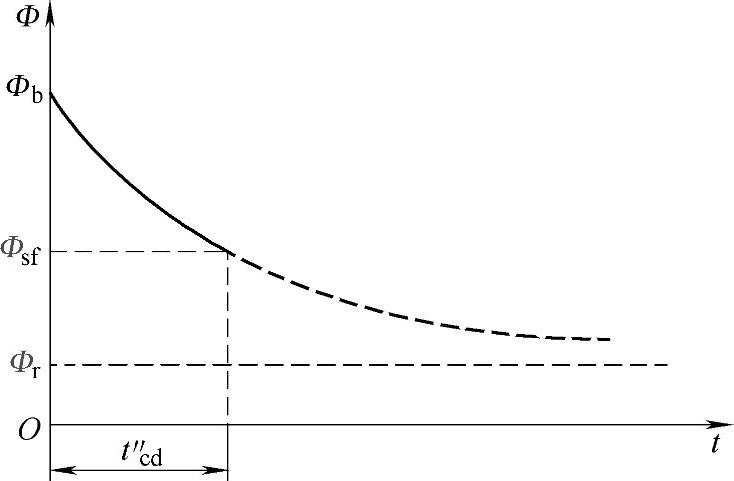
图6-27 磁通衰减曲线

（2）释放运动时间t″_yd 衔铁开始运动以后，电流（或涡流）的变化规律比较复杂，和计算吸合运动时间一样，必须作一些简化。设衔铁释放运动时不计电磁吸力，即设F_d=0，则衔铁只在反力的作用下释放，这时，衔铁的运动方程可写为

式中 m——衔铁及阀芯等运动部件的质量（kg）；

v——衔铁的运动速度（m/s）；

F_f——电磁铁的反力（N）。

若已知F_f随δ变化的规律F_f=f（δ），即可代入上式求解t″_yd。对于高速电磁开关阀其反力主要是复位弹簧，因此可假设F_f的变化规律为线性，即

F_f=F_fb-kx （6-71）

式中 F_fb——衔铁在吸合位置时的反力（N）；

x——衔铁返回运动的行程（m）；

k——复位弹簧的刚度（N/m）。

于是可求得

式中 F_fk——衔铁打开位置时的反力（N）。

在这里分析时，仅考虑了复位弹簧的反力，实际上在这个阶段，仍然有涡流引起的阻滞释放运动的阻力，还有剩磁造成的滞后电磁阻力限制释放运动的过程。

通过上述的分析计算可以看出，要提高高速电磁开关阀的快速性就要减少电磁铁的吸合时间（包括t_c′_d，t_y′_d）和释放时间（包括t″_cd，t″_yd），为此，可采取以下措施：

1）从式（6-54）可知，要减t_c′_d就要减小T=L/R这个时间常数。对于高速、高压电磁开关阀，由于多用盘式电磁铁，这时一般工作气隙都很小，这时可应用麦克斯韦电磁吸力公式计算电磁铁吸力，即

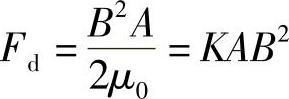
式中 F_d——电磁吸力；

A——电磁铁工作气隙对应的面积；

μ₀——空气的磁导率，μ₀=1.25×10^-6H/m。

而磁感应强度B正比于励磁线圈的安匝数，反比于磁极面积和磁路磁阻，即

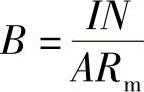
由此得

而线圈电感

所以

与工作气隙的磁阻相比，铁心磁阻是非常小的，因此有

式中 μ₀——空气的磁导率；

δ——工作气隙长度。

由此得

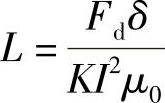
最后得

式中 I²R——输入电磁铁的能量。

对于给定条件的高速电磁铁，其工作气隙δ是受到工作条件要求的，所以δ的减小是有限度的。

由上式可知，减小时间常数T，就要增大能量输入P_W=I²R，就是对电磁铁进行激励，通过加快电磁铁线圈电流上升速率来减小时间常数T，从而缩短电磁铁的吸合触动时间t_c′_d。

另外，为减少时间常数T=L/R，应减少电磁铁励磁线圈的匝数N，因为线圈的电感L为

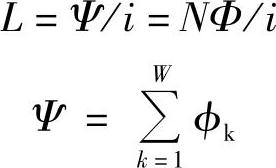
式中 Ψ——线圈各匝相交链的磁通总和，为线圈的磁链。

若通过各匝的磁通相等，并等于Φ，则Ψ=NΦ。显然，N的减少，可减少线圈的电感，加速线圈断电时其中电流的衰减过程，使电磁铁的释放触动时间减少。N的减少，也可使吸合时间减少，但N的减少将使线圈磁通势IN下降。因此，为了保证足够的电磁吸力，只有加大线圈电流I，即对电磁铁进行强激励。

2）减少反力F_f，可使吸合时间t_y′_d减少，但反力减少会影响释放运动时间的减少，所以要兼顾两者，折中考虑。

3）减少电磁铁动铁心、即衔铁行程δ_K，可使t_y′_d减少，但δ_K减少，意味着电磁铁驱动的阀芯开口要减小，这要影响阀的工作流量的要求。

4）减少运动部件的质量，包括衔铁、阀芯等，可减少t_c′_d，t″_yd。

5）减少涡流可使t_c′_d，t″_cd减少，因此尽管是直流电磁铁，也常常要用电阻系数高的硅钢片来叠制成铁心。

高速、高压电磁开关阀，不仅仅要求能高速、高频响地启闭运行，而且由于柴油机高压喷射的要求，其工作压力要达到120～220MPa，甚至更高。因此，高速高压电磁开关阀所用的电磁铁必须具有足够的电磁作用力储备。

一方面，足够的电磁作用力或电磁吸力可保证电磁铁衔铁及其阀芯运动时有足够高的加速度，加速电磁阀的关闭，而且即便是衔铁及其阀芯的反作用力由于偶然因素变大时，足够大的电磁作用力仍能确保阀芯关闭加速度基本不变，确保电磁阀快速响应的可靠性，保证喷油定时的准确性。

另一方面，足够的电磁吸力为电磁开关阀的高压密封提供了保障。高速、高压的二位二通锥阀式电磁开关阀，其结构如图6-28所示。该电磁阀形成高压燃油的密封需要有两个密封面：一为圆柱形滑阀与阀体内孔之间的径向间隙密封；另一个是菌状锥形阀与阀座孔之间的密封。滑阀与阀体内圆柱孔之间的间隙密封，取决于间隙的大小，密封长度，而锥形阀与阀座之间的密封取决于电磁铁的吸力和各种反力的大小。只有电磁铁产生足够的电磁作用力才能保证电磁阀可靠的高压密封。

图6-28 二位二通锥阀式电磁阀的结构

因此，超高压高速电磁阀的驱动电磁铁的结构形式选择非常重要。目前，柴油机各类电控喷油系统中用的电磁铁主要是两类：螺线管式电磁铁和盘式电磁铁。螺线管式电磁铁的电磁吸力含有漏磁通产生的螺线管力，而且对于有平顶座的螺线管式电磁铁，在闭合位置附近的螺线管力及衔铁端部的吸力均得到加强，可使电磁吸力特性变陡，而且当电磁铁处于打开位置时，尽管工作主气隙δ上主磁通Φ_δ产生的端面吸力F_δ下降迅速，但由漏磁通Φσ产生的螺线管力F_dσ却变化不大。因此，它适于需要衔铁或阀芯行程（或开口）较大的场合，而且螺线管式电磁铁结构简单，径向尺寸较小。盘式电磁铁吸合面积大，而行程小，吸力特性非常陡，因此，随着衔铁的吸合，亦即锥阀芯的关闭，电磁吸力迅速增长，因此可获得极大的电磁吸力，以满足高压高速电磁开关阀的需要。因此，目前盘式电磁铁在各类柴油机电控喷油系统中应用较多，螺线管式也有不少应用。