电磁铁能否可靠的工作取决于其吸力特性与反作用力特性配合得是否恰当。所谓吸力特性就是在某一线圈磁通势IN（或线圈电压U）时，作用在衔铁上的电磁吸力Fd与衔铁行程（或工作气隙）δ关系：Fd=f（δ），IN=常数（或U=常数）。所谓反作用力特性指的是衔铁运动时必须克服的阻力Ff与行程δ的关系，即Ff=f（δ）。因此，必须对电磁吸力进行计算。为此，先分析磁场的能量。
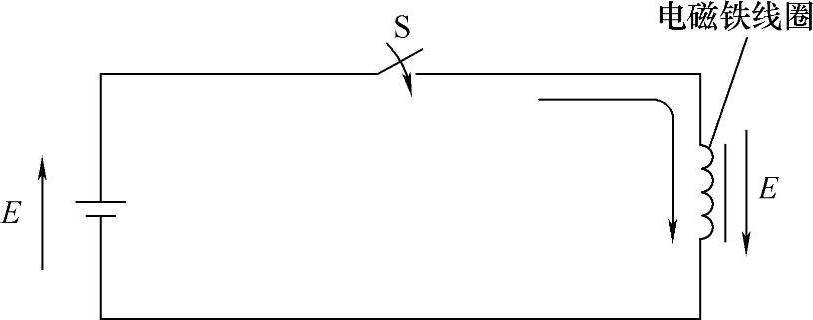
图6-6 磁场的建立过程
1.磁场的能量
磁场的能量是在建立磁场的过程中从产生磁场的外电源或其他能源中转化来的。在图6-6所示回路中，合上开关S时，电磁铁线圈中的电流I并不能立即增大，而是逐渐增大至最后的稳定值Iw（Iw=E/R，E为外电源的电动势，R为回路总电阻）。这是因为，在建立磁场的过程中，磁通的增大会在线圈内感应而产生一个反电动势e。e的作用方向是企图阻止电流的增大，而其大小正比于通过各匝线圈的磁通量对时间的变化率的总和，即
式中 Φk——通过第K匝线圈的磁通量（Wb）；
N——为线圈总匝数。
将上式适当转换，得
式中 Ψ——与线圈各匝相交链的磁通总和，其定义为：线圈的磁链，若通过各匝的磁通相等并等于Φ，则Ψ=NΦ。
外电源E在克服这个反电动势的过程中提供了能量，其能量转换关系可从电路方程求得
Eidt=i2Rdt+idΨ （6-19）
上式中，左边Eidt代表外电源在dt时间内所提供的能量。这个能量中的一部分转化为热能，消耗在回路电阻R内，即i2Rdt，而剩下的一项idΨ就代表外电源在dt时间内克服反电动势所供给的能量。根据能量守恒定律，如果电磁铁的衔铁保持不动（即不做任何机械功）并忽略导磁体内的涡流和磁滞损耗，它就必然代表磁场中增加的储能。
若线圈电流由零增大到某一值I1，磁通（或磁链）相应地由零增大到Φ1（或Ψ1），则磁场所获得的能量为Wc。而
若通过各匝的磁通相等并等于Φ，则得
图6-7 图解积分法求磁能
a）已知磁系统的励磁特性Ψ=f（i） b）已知磁系统的磁化曲线Φ=f（iN）
如果已经通过磁路计算求得磁系统的磁化曲线Φ=f（iN），或者求得其励磁特性Ψ=f（i），如图6-7所示，则Wc即正比于图6-7中的阴影面积。值得指出的是，磁系统内的储能只和其磁化曲线的形状以及最终的Φ1（或Ψ1）及I1有关。而和其建立过程中电流（或磁通）随时间增长的快慢并无关系。
Wc也可表示成其他形式，例如当磁系统中铁磁材料并不饱和时（或者在空心线圈时），Φ（或Ψ）与i的关系为线性，则式（6-20）及式（6-21）可以转化为下列形式：
定义Ψ（或NΦ）与i的比例系数为线圈的电感L，即
显然，若Ψ与i的关系为非线性，则L不是常数。但是若Ψ-i的关系为线性，则L为常数。因此，可用下式计算磁能（单位为J）
至此，我们讨论了电磁铁的衔铁保持不动时，电能和磁能的转化关系。下面将进一步讨论当衔铁在电磁吸力的作用下移动一个距离而做机械功时，电能、磁能和机械功之间的转化关系，从而导出电磁铁吸力公式。
2.电磁铁吸力计算的一般公式
图6-8a拍合式磁系统中，当主工作气隙为δ1时的励磁特性Ψ=f（i）如图6-8b所示，当线圈电流为I1时，线圈磁链为Ψ1。此时磁系统内的储能为Wc1，Wc1正比于面积Aoac，即
图6-8 电磁铁的能量转换与吸力
a）拍合式磁系统 b）励磁特性
若此时作用于吸片上的电磁吸力为Fd1，其正方向为向下，即使工作气隙减小，如图6-8a所示，则为了确定该吸力，假设吸片在该吸力的作用下移动一个微小的距离Δl，此时气隙将由δ1减小为δ2，而Δl=δ1-δ2，在吸片移动的过程中，保持线圈电流不变，则由于气隙减小，磁阻减小，磁路中的磁通和线圈磁链将会增大。当δ=δ2时，磁链为Ψ2，Ψ2可由δ=δ2时的Ψ=f（i）求得。如图6-8b所示。在吸片移动的过程中，磁系统又要从电源内吸收一部分能量，用Wm表示，即
即Wm正比于图6-8bAcabd。
到目前为止，磁系统由外电源总共吸收了Wc1+Wm的能量。显然，这些能量不是都储藏在磁系统内。因为，在吸片移动的过程中，电磁吸力做了一定的机械功，因此必然有一部分磁能要转变为机械能。实际上，当气隙为δ2，磁链为Ψ2时，储藏在磁系统内的磁能为Wc2，而Wc2=Aobd。
因此，电磁吸力所做的机械中ΔW即可根据能量守恒定律由下式确定，即
ΔW=Wc1+Wm-Wc2=Aoac+Acabd-Aobd=Aoab
即ΔW正比于图6-8b中的阴影面积。
求得ΔW后，即可确定吸片在Δl的行程所受到的平均电磁吸力Fdp，因为
ΔW=FdpΔl
因此
考虑到
Δl=δ1-δ2=-（δ2-δ1）=-Δδ，
由此可得
如果Δδ趋向于零，该Fdp就等于δ1时的吸力Fd1。
但是，用以上方法推导的吸力计算公式（6-25）只是原理性的，在实际应用该公式计算吸力时并不方便。不过，根据这个原理可以推导求得一些比较实用的吸力计算公式如下：
1）若假定在吸片（或衔铁）Δl的移动过程中漏磁通并不改变，例如拍合式电磁铁就近似于这种情况，则可用下式计算电磁吸力（单位为N），即
式中 uδ——该气隙的磁压降（A）；
Λδ——该气隙的磁导（H）；
δ——气隙大小（m）。
电磁吸力Fd的正方向取为δ减小的方向。该公式的推导过程从略。此外，若有漏磁存在，但漏磁不随气隙的改变而变化，上式仍可适用。
2）对于旋转式电磁铁，往往需计算的是电磁力矩Md，此时，当衔铁旋转Δα弧度时所做的机械功
ΔW=MdpΔα
式中 Mdp——Δα弧度内电磁力矩的平均值。
所以
同理可求得计算电磁力矩的实用计算公式为
3）利用麦克斯韦公式求的另一个计算电磁力的公式为
然而，实用上并非在任何场合都可用式（6-26）、式（6-28）这两种电磁力公式中任何一种进行计算。例如，当气隙值甚小时，除非气隙磁导能以解析公式表示，一般不宜采用能量平衡电磁力公式（6-26）。因为dΛδ/dδ有时颇难计算准确，以致电磁力计算产生较大误差，但是这种衔铁接近闭合场合，气隙磁场一般相当均匀，故可用麦克斯韦公式求得相当准确的结果。当然，即使气隙较大，在已知气隙中磁感应强度的分布规律B=f（s）时，同样可采用麦克斯韦电磁力公式。
3.电磁铁的吸力特性和负载特性
电磁铁是一种依靠电磁系统产生的电磁吸力，使衔铁对外作功的一种电动装置，其基本特征可表为衔铁在运动中所受到的电磁力Fd与它的行程δ之间的关系，即Fd=f（δ）。这个关系称为吸力特性，对于比例电磁铁，要求它具有水平的吸力特性（见图6-9的曲线1）。对于力矩电动机，其吸力特性用电磁转矩与衔铁转角的关系表示。
图6-9所示为普通开关电磁铁与比例电磁铁的静吸力特性。由电磁吸力公式（6-26）可知，电磁铁的吸力与气隙磁压降uδ和气隙磁导变化率dΛδ/dδ有关，而这两者又与线圈磁通势IN和气隙大小δ有关。因此对于某一形式的电磁铁，其电磁吸力Fd是IN和δ的函数，即Fd=f（IN，δ）。在某一磁通势下，即IN=常数，电磁吸力Fd与δ的关系Fd=f（δ）称为电磁铁的静吸力特性。显然不同的磁通势，Fd=f（δ）也不相同，因此得到一组曲线。当衔铁在运动过程中，由于会在线圈中感应电动势，使线圈电流发生变化，即IN≠常数，这时Fd与δ的关系为动吸力特性。在衔铁的实际运动过程中，只存在动态吸力特性，静态吸力特性只是衔铁无限缓慢移动时的一种特例。由于动态吸力特性与负载有关，以致同一电磁铁也会有不同的动态吸力特性。习惯上把静态吸力特性作为电磁铁的吸力特性。在电磁铁的运动过程中，必然要克服机械负载和阻力而做功。对于开关电磁铁在吸合过程中，电磁吸力特性曲线应在负载反力曲线的上方，而在释放运动中，负载反力又必须大于剩磁产生的电磁力。但在吸合过程，电磁吸力也不宜超过负载反力太多，否则会导致吸合撞击。
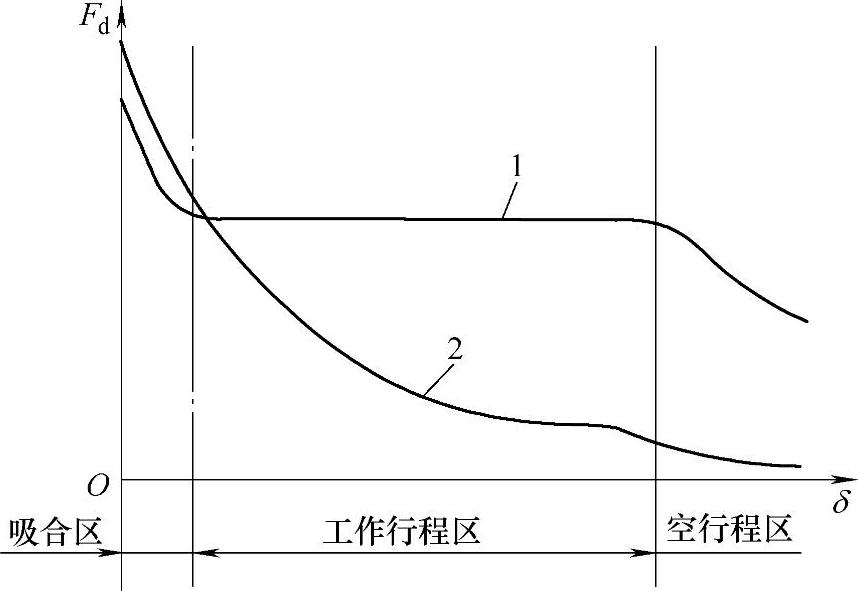
图6-9 电磁铁的静吸力特性
1—普通开关电磁铁 2—比例电磁铁
对于比例电磁铁，由于在工作过程中，电磁力总是与负载反力相平衡，参与工作的吸力特性曲线有很多条，而负载多为弹簧负载，所以它工作时吸力特性与负载反力特性的配合情况如图6-10所示。负载弹簧的特性曲线与多条吸力特性曲线相交，对应不同的输入电流。电磁铁的吸力特性水平上下平移，而它与弹簧特性曲线的相交点便是对应电流下的工作点。由图6-10中可以看出，当电流I改变时，工作点也改变，比例电磁铁正是利用这一特性实现电—机械信号的比例转换。
（1）吸入式电磁铁的静吸力特性 吸入式电磁铁就是螺线管式电磁铁。在柴油机电控技术中所应用的吸入式电磁铁基本上分为两类：一种是开关型的，但必须是高速开关型的。另一类即是比例电磁铁，也即线性电磁铁。下面先讨论最基本的平顶型的螺线管电磁铁。
图6-10 比例电磁铁的吸力特性与负载特性配合
吸入式电磁铁中（图6-11a），可动铁心侧面到壳体之间的漏磁通Φσ是直接随动铁心的移动而变化的，因此就不能单纯用公式（6-26）计算吸力，此时可以将作用于可动铁心的电磁力Fd看成是由两部分力所合成，即
Fd=Fdδ+Fdσ （6-29）
式中 Fdδ——通过主工作气隙δ的主磁通Φδ所产生的端面吸力；
Fdσ——漏磁通Φσ1与线圈导线电流作用而产生的电动力，Fdσ也称螺线管力。
端面吸力Fdδ可用公式（6-26）计算，即
而螺线管力Fdσ可以近似用下式计算，即
式中 IN——线圈磁通势（A）；
lk——线圈长度（m）；
Φσ1——可动铁心部分总的漏磁通（Wb）。
公式（6-31）的推导如下：
(www.xing528.com)
图6-11 吸入式电磁铁
a）铁心为平顶 b）铁心为锥顶 1—可动铁心 2—上端盖 3—线圈 4—台座（也称静铁心） 5—隔磁套 6—壳体 7—下端盖
图6-12为吸入式电磁铁通过轴线的一个剖面。在其上半部画出了可动铁心段分布的漏磁通。该漏磁通对圆环导线产生电动力，力图使线圈右移（左手定则），而其反作用力即使动铁心左移。设作用于截面积为dxdr，半径为r的微元中那部分线圈中的电动力dFd′σ，而由安培定律得
dFd′σ=I（lx×Bx）
式中 Bx——漏磁感应强度（T）；
lx——微元中通电导线的长度（m），方向为导线中电流的方向；
I——线圈电流（A）。
若在dx段内的漏磁通为dϕσ，则
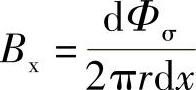
若线圈总匝数N，长度为lk，厚度为r2-r1，则
因为径向的漏磁通各处都和导线垂直，因此有
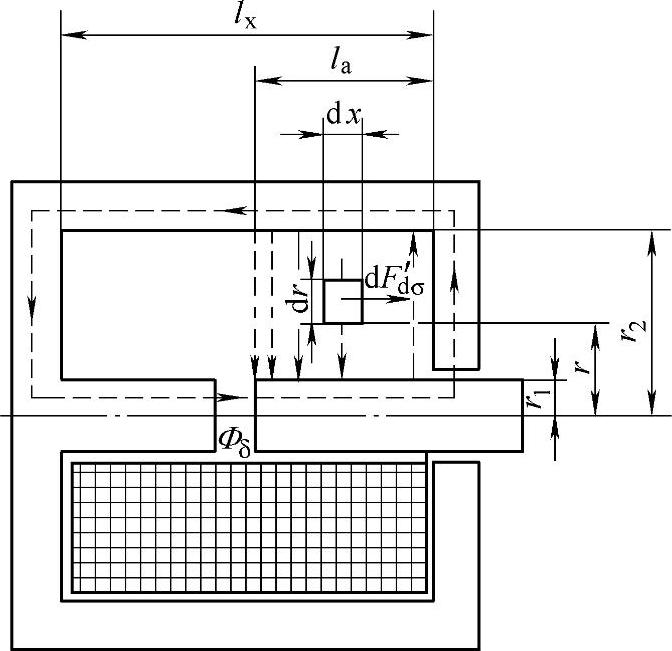
图6-12 螺线管力
在la这一段内作用于线圈上的总的电动力Fd′σ为
式中 Φσ1——la段内总的漏磁通。
Fd′σ的反作用力Fdσ即作用于动铁心，使动铁心向气隙减小的方向运动。
Φσ1可表示为
式中 g——单位长度漏磁导（或称比磁导），因此
将式（6-30）及式（6-32）代入式（6-29）最后得
由此式可得出以下几点结论：
1）若铁心为平顶，则当δ不是很大时，可以认为
（A为极面面积），而
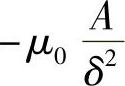，因此Fdδ=f（δ）是双曲线型，（这里忽略铁磁阻和工作气隙的磁阻，则Uδ近似等于线圈磁通势IN，而不随δ变化）。随δ增大，Fdδ很快下降。但是，当δ变化时，漏磁通Φσ1却变化不多（因为δ的变化是相对la来说是不大的），所以Fdσ不会因为δ的增大而减少很多，而且，在打开位置时，螺线管力所占的比例更大，因此，它适用于需要铁心行程较大的情况。
2）螺线管力Fdσ与线圈磁通势（IN）2成正比，因此，增大IN就可以增大Fdσ，而不受磁路饱和所限。这就使吸入式电磁铁适用于短时产生较大的吸力，因为线圈短时通以很大的电流并不会发热过甚。
3）铁心（及台座）端面的形状对吸力特性有较大的影响。锥顶铁心的吸力特性比平顶的平坦，如图6-13所示。这是因为锥顶铁心的气隙磁导Λδz和其导数dΛδz/dδ都比平顶的Λδp和dΛδp/dδ大
。而当δ较大时，可以认为线圈磁通势绝大部分降落在主工作气隙上，即uδ=IN。
因此，锥顶的吸力要比平顶的大。但是，当δ较小时，磁铁和非工作气隙中的磁压降就不能忽略，这时，由于Λδz＞Λδp，锥顶气隙磁压降就会比平顶的小。很明显，锥角α愈小，吸力特性就愈平坦。当δ较大时，吸力也愈大，所以适应于较大行程的情况。比例电磁铁就是基于此特性而工作的。但这种形式的比例电磁铁的吸力特性并不理想，理想的比例电磁铁的吸力特性应是水平吸力特性，即要求它的电磁吸力与行程无关，只取决于线圈电流I的大小。
目前应用广泛的是所谓盆底止座结构的比例电磁铁。盆底止座结构的比例电磁铁，实质是在基本平顶吸入式电磁铁的主工作气隙区域设置了一个由导磁材料制成的磁分路器。这样可以有效地改变吸力特性的形状，使其变得平坦。如图6-14所示，吸入式磁系统的磁分路器就是台座的一部分。此时将台座做成盆形，其盆边就起磁分路器的作用，盆边的高度为b，它与铁心间形成圆环状气隙δr。
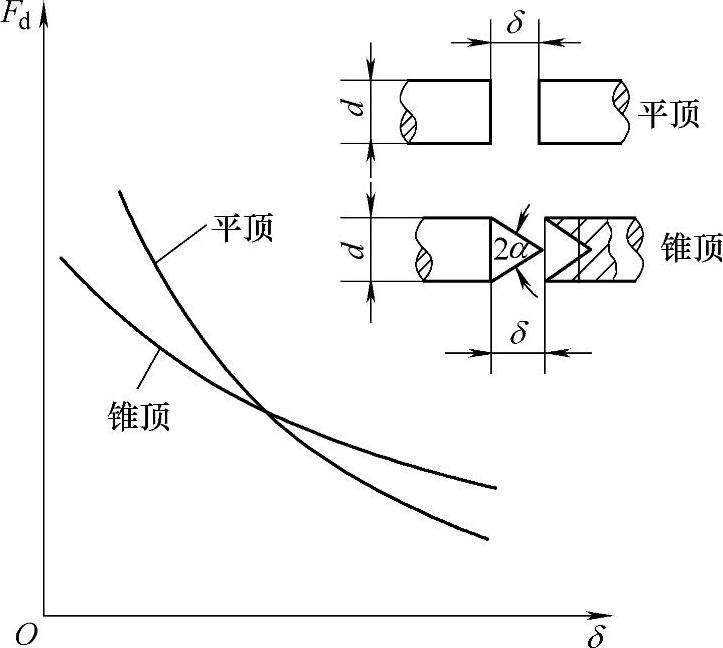
图6-13 吸入式电磁铁静吸力特性
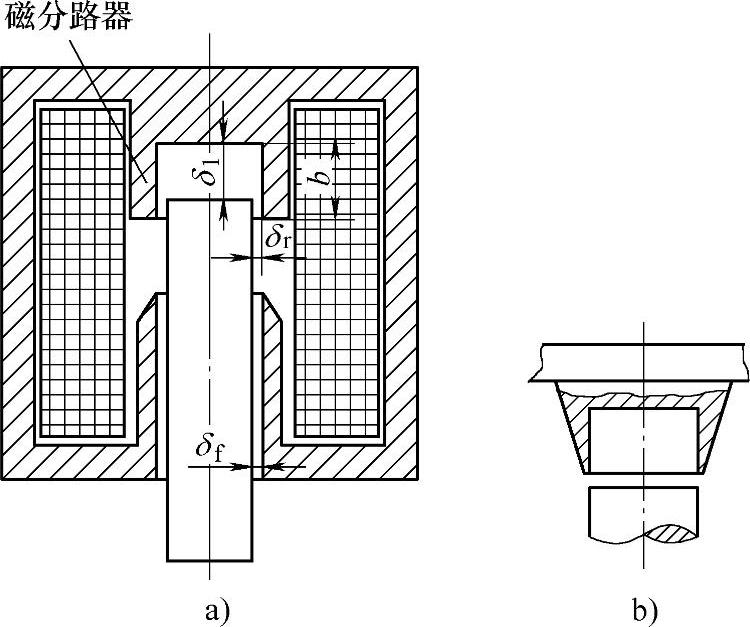
图6-14 具有磁分路的吸入式电磁铁
a）非饱和型 b）饱和型（仅画出台座和铁心端部）
由吸力计算公式（6-26）可知，电磁铁的吸力特性取决于主工作气隙上的磁压降uδ以及其气隙磁导Λδ随气隙δ（或衔铁行程）变化的情况。电磁铁在没有磁分路器时的吸力特性，如图6-15中曲线1，而在设置了磁分路器后的吸力特性如图6-15中曲线2。
为了便于分析，在图6-16a中绘出了磁系统的原理等值磁路图，并在图6-16b中绘出了吸入式主工作气隙各部分磁导的示意图及局部等值磁路图。图中Λδ，Λf及Λk分别为主工作气隙δ，非工作气隙δf以及导磁体的磁导，Λδ则由磁极相对端面间的主磁导Λ0，衔铁与磁分路器之间的散磁导Λ2，以及磁分路器本身的铁磁导Λtf，串、并联组和而成。当气隙较大时（δ＞b），主工作气隙的磁阻远大于非工作气隙和导磁体的磁阻，所以线圈磁通势IN绝大部分降落在主工作气隙上，即uδ=IN。另一方面，由于在气隙区加入了磁分路器，Λδ与dΛδ/dδ必然增大，因此，使电磁吸力增大，即当δ＞b时，特性2高于特性1。当气隙减小到δ＜b，即当吸入式的动铁心开始进入盆形台座的内腔时，形成的圆环状气隙δr，使磁导Λ2增大，并分走相当一部分气隙磁通。铁心愈深入盆腔，分走的磁通也愈多，这部分磁通虽然也能产生吸力，但其dΛ2/dδ近似为常值。另一方面，Λ2的增大导致Λδ增大，以致其数值可以和Λf相比较了。这时线圈磁通势重新分配，使uδ减小。综合以上两个原因，吸力特性将由上升变为下降，形成了第一个转折点δ1，而且δ1=b。磁路愈饱和，或非工作气隙δf愈大，则下降的趋势更为明显（因uδ减小更多）。当工作气隙继续减小到磁极端面很接近时（例如δ2），由于端面间的主磁导Λ0大大增加，气隙磁通的大部分通过Λ0，又因为dΛ0/dδ在δ很小时增加很快，致使端面吸力大大增加，吸力特性也就再度上升，形成第二转折点δ2。
图6-15 具有磁分路器与没有磁分路器的吸力特性
1—没有磁分路器的吸力特性 2—具有磁分路器的吸力特性
图6-16 具有磁分路器时的等值磁路图
a）磁系统的原理等值磁路图 b）吸入式磁系统的主工作气隙各部分磁导示意图及等值磁路图 c）具有磁分路器的吸入式电磁铁的吸力特性
改变磁分路器的厚度b、气隙δr或磁分路器的饱和程度就可以有效改变吸力特性的形状。图6-14a为非饱和性，即具有等截面积的盆边，其吸力特性已如前述，具有明显的马鞍形，如图6-16c中非饱和型曲线，而图6-14b为饱和型，即具有变截面积的盆边（图中只划出台座及铁心端部）。由于盆边的截面积在端部很小，所以只要不大的分路磁通就会使这部分达到磁饱和，从而限制了分路磁通，阻止吸力下降，而当动铁心进入盆口后，饱和的磁分路起了一个特殊调节器的作用，使吸力特性在以后的一段行程内保持不变，直到动铁心端接近盆底端面，端面吸力大大增加，使吸力特性再度上升，如图6-16c中饱和型曲线。
（2）旋转式电磁铁的吸力特性 旋转式电磁铁的特点是：线圈通电后，衔铁即动铁心的运动方向不是沿着磁力线的方向，而是垂直于磁力线的方向。旋转式电磁铁的衔铁转动时，通常漏磁通的变化并不大，因此，可以用公式（6-27）来计算电磁力矩。电磁力矩的方向总是力图使衔铁运动到使整个磁路内磁阻为最小的位置。因此，在图6-17所示的例子中，电磁力矩的方向为逆时针方向。当衔铁转动时，气隙δ0并不变化，但气隙面积A将发生变化，如不考虑散磁，则气隙磁导Λδ可由下式计算，即
式中 α——极面对转轴所夹的角度（rad）；
r0——极面圆弧的半径（m）；
b——衔铁厚度（m）。
因此
因为衔铁旋转时上下两个气隙的极面都发生变化，因此，电磁力矩为
式中 uδ——每一个气隙上的磁压降（A）。
由式（6-34）可见，若忽略导磁铁磁阻，则当线圈磁通势IN为常数时，uδ和Md为常数。因此，电磁铁的吸力特性为一水平直线，如图6-18所示。显然改变磁通势IN，则可得到不同的Md直线。因此，如果在旋转电磁铁的衔铁上装上复位弹簧，则就可使衔铁（或转子）在与Md平衡时，停留在某一位置上。因此，与比例电磁铁一样，可通过控制励磁电流I，实现衔铁转角的连续的、成比例的调节与控制。
图6-17 旋转电磁铁原理图
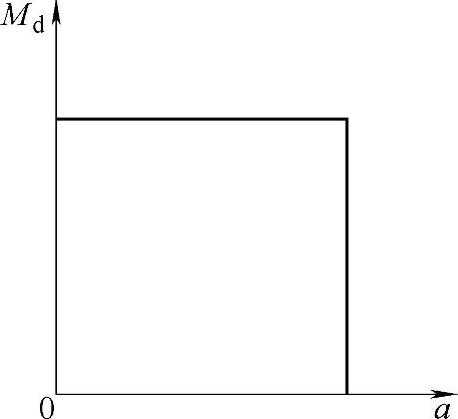
图6-18 旋转电磁铁静吸力特性
如果要求衔铁的旋转角度比较大时，则衔铁外形不再是圆弧，也就是说，在衔铁转动时，气隙δ0不能不变。而为某一种其他曲线形状，如螺旋线形、双曲线形等。这时衔铁的旋转角度可达120°～150°。下面介绍在这种情况下的吸力计算公式。
图6-19为一般情况下的一对磁极，其中气隙δ为角度φ的函数，即δ=f（φ）。设衔铁一个极的极距为τ，定子极所张的角度为φd，极宽为b，定子极面半径为rd，衔铁极面最大半径为r0，而rd-r0=δ0，δ0为最小间隙。
计算气隙磁导时忽略散磁导，则
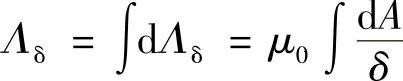
式中 dA=brdφ。
若δ相对于r很小时，则
dA=br0dφ
因此有
而
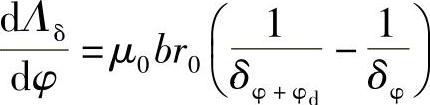
所以一对磁极所产生的电磁力矩为
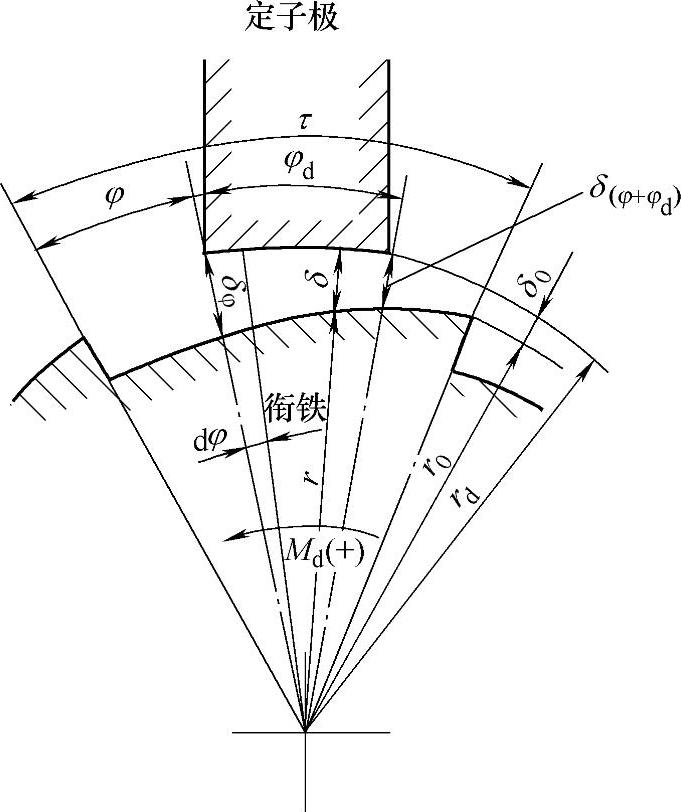
图6-19 求旋转电磁铁的吸力
将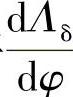
代入上式，即得
若令
式中 Md0——为一不随φ而变的常数。
则式（6-35）可写为
Md=Md0f（φ） （6-36）
式中
f（φ）称为特征函数，只要研究了f（φ）就可知道Md与φ转角的关系。
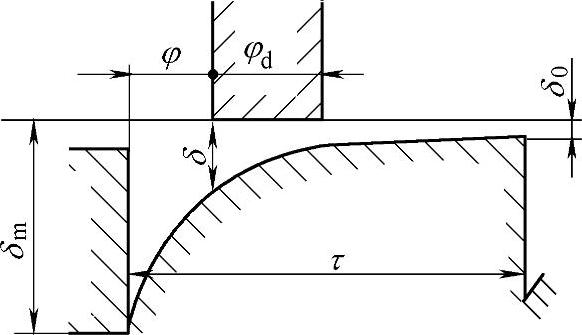
图6-20 例题图
例题 旋转电磁铁的气隙按双曲线规律变化，即
，
。如图6-20所示，试求其吸力特性。
解：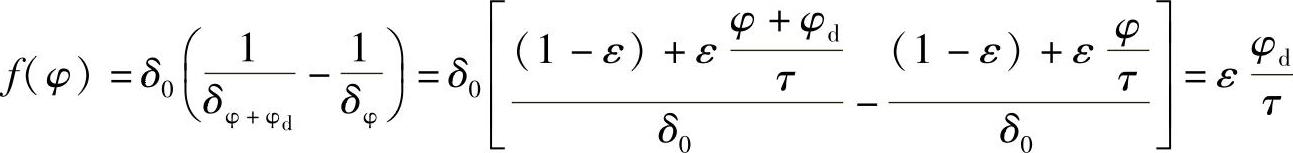
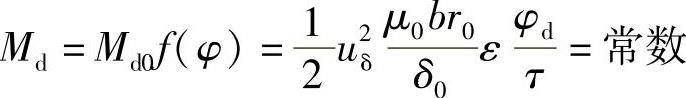，即Md=c，所以在忽略磁阻，则当线圈磁通势IN为常数时，uδ和Md为常数，因此电磁铁的吸力特性为一水平直线。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
