电磁场基础及磁位概念的引入

1.磁场

任何运动电荷或电流，在周围空间内产生磁场，并对场中其他运动电荷或电流产生力的作用。运动电荷或电流的相互作用是通过磁场和电场来传递的。磁场是统一的电磁场的一个方面。磁场用磁力线或磁通来描述。在磁场中通过一给定面积的磁力线称为通过此面积的磁通量，或简称磁通Ф，单位为韦伯（Wb）。

而表示磁场强弱的方法有两种：

第一种方法是单位面积上所通过的磁通量，称磁感应强度B（单位为Wb/m²），这是一个矢量，其大小可用公式表示为

式中 A——垂直于磁力线的给定面积。

另一种方法是规定任何磁介质中某一点的磁感应强度B和磁导率_μ的比值称为磁场强度H。这也是矢量，用公式表示为

磁场强度的单位是安培/米（A/m），磁导率的单位是亨利/米（H/m）。

2.安培环路定律（也称“全电流定律”）

关于磁场（B或H）与场源（宏观电流）之间的关系可以由物理学中的毕奥—萨伐尔定律来确定，也可以安培环路定律来确定。这两个定律都是在大量实验的基础上总结出来的，这里主要介绍的是应用较多的安培环路定律。

安培发现在任何磁场中，矢量H沿任何一封闭回线的线积分等于穿过此回线所界定之曲面的电流的代数和，如图6-1所示。用数学形式表示为

式中 H——回线上某点（如A点）的磁场强度；

dl——A点附近沿回线一小段的距离矢量；

θ——H和dl之间的夹角。

∑I——穿过此回线所界定的曲面的电流的代数和，式中电流I的正负视其方向与所选回线方向是否符合右手螺旋法则而定，如图6-1所示情况，I₁为正，I₂为负，I₃未穿过该曲面，因此不计入，所以∑I=I₁-I₂。

这个规律就叫安培环路定律，后经麦克斯韦发展为全电流定律，即∑I中不但包括传导电流也包括位移电流。

显然，在各向同性的均匀线性介质空间内，当磁场对称分布时，应用安培环路定律计算磁场要比应用毕奥—萨伐尔定律方便得多。理论和实践均可证明，式（6-3）不仅适用于均匀介质，也适用于非均匀介质。

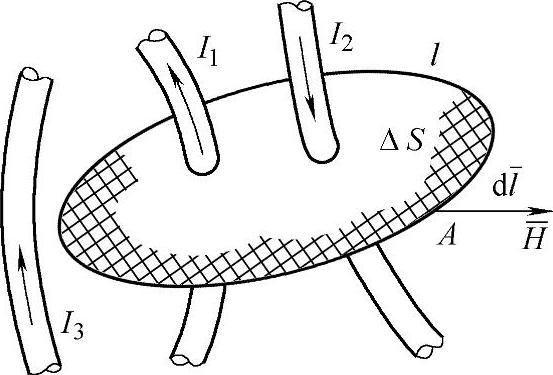
图6-1 安培环路定律

3.标量磁位、等磁位面及磁场的图形

为了便于对磁场进行研究，也可以模仿电场中的电位，引入磁位（指标量磁位）的概念。在某一特定的空间内（见下述），恒定磁场中任意一点的磁场强度H与标量磁位u之间的关系可由下式表示：

H=-gradu 或 H=-▽u （6-4）

式中 gradu或▽u——磁位的梯度。

因此，场中某点P相对于参考点0的磁位u_p是

一般认为参考点的磁位u₀=0，而场中某两点a和b之间的磁位差是u_ab为

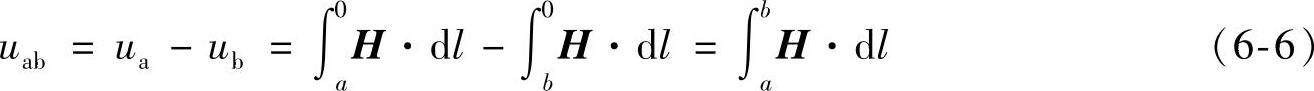
例如，在均匀磁场中（图6-2），沿磁力线方向求以上线积分得

u_ab=Hl_ab （6-7）

而在非均匀磁场中，若假设沿磁力线方向的微小段Δl_i上的H_i为常数，则该微小段上的磁位差为

u_ab=H_iΔl_i （6-8）

通常将磁场中磁位相等的点连成的曲面称为等磁位面，而对于不同磁位就会有不同的等磁位面。如图6-2中的a—a，b—b，c—c面，因此，在磁场中形成一组等磁位面。可以证明，等磁位面（或线）必然与磁力线正交。

4.磁路

像电流在电路中运动一样，磁通也沿一定的磁路形成闭合的回路。什么叫磁路？凡是磁通（或磁力线）所经过的闭合回路就叫磁路。一般情况下，磁力线散布在整个空间，不容易找到一条磁通比较集中通过的磁路。但是，在一般电磁机构中，为了获得较大磁通，通常采用铁磁材料制作零件，使磁通主要集中在导磁材料中，这样可形成一个确定的磁路，使计算简便了。计算磁路所用到的一些概念和定律，如磁通势、磁通、磁阻、磁位差、磁路的欧姆定律和克希荷夫二定律都是直接从磁场的概念和定律转化得来的，但是在形式上与电路非常相似。

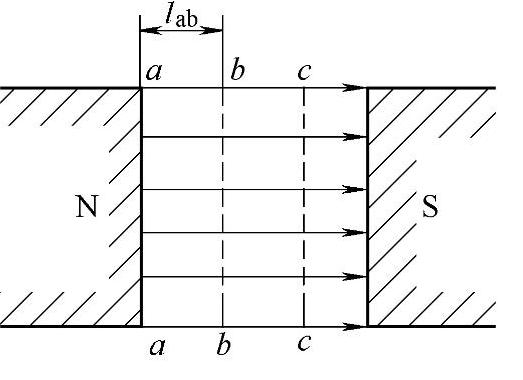
图6-2 均匀磁场中的磁力线和等磁位面

（1）磁通势、磁通、磁阻和磁压降 图6-3a所示是一个最简单的磁系统。它只有一个圆环状铁心，环上绕有N匝的线圈。当线圈通以电流I后，绝大部分磁力线都会集中在磁导率很高的铁心之中（若线圈均匀而又紧密地绕在整个圆周上，则磁通实际上几乎全部局限在环内）。

若圆环的内外径之差远比平均直径小，则可以认为磁通在横截面A上的分布是均匀的。因此，铁心各处的B（或H）可以认为相等。设圆环平均周长l_p应用安培环路定律，并注意到各处的H和dl同方向，即cosθ=1，因此得

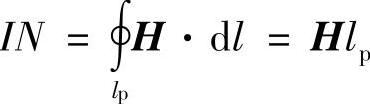
考虑到

H=B/μ(www.xing528.com)

式中 μ——铁心材料的磁导率。

B=ϕ/A

代入上式则得

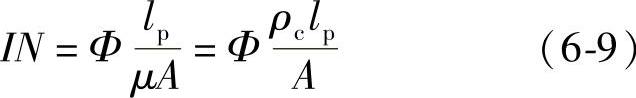
式中 ρ_c——磁导率μ的倒数，称为“磁阻系数”，即ρ_c=1/μ。

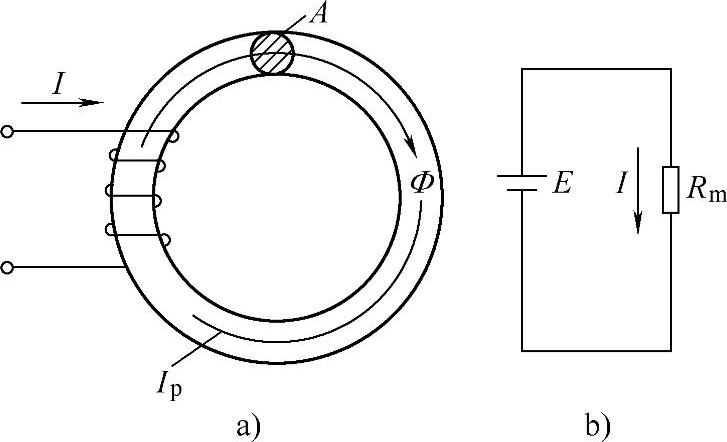
图6-3 磁路和电路的对比

a）磁路 b）电路

将线圈中电流I与匝数N的乘积IN称为“磁通势”，并将磁通势与磁通Φ之比定义为磁阻R_m，即

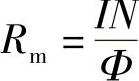
则对于均匀磁场，由式（6-9）有

因此，磁路中磁通与磁通势和磁阻的关系即可表示为

这个关系就称为磁路的欧姆定律，它和电路中的全电路欧姆定律在形式上很相似。

磁通势的单位为安，但习惯上往往称它为安匝，以便和电流相区别。在磁路计算中，比较习惯于应用磁导Λ，磁导就是磁阻R_m的倒数，即

磁导的单位为H，1H=Wb/A。

在电路中，电阻两端的电位差U叫作电阻压降，简称电压降，可表示为

U=IR

同样，在磁路中，磁阻两端的磁位差U_m叫做磁压降，也可表示为

U_m=ΦR_m （6-13）

因为由式（6-7）得

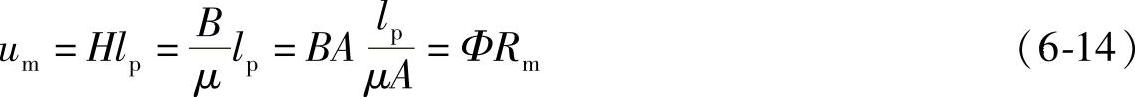
磁路中，磁场强度H具有另一种含义，即由式（6-14）H=ΦR_m/l_p，因此，可以将H看成为磁路单位长度上的磁压降。

因为磁路和电路在计算上有相似之处，所以分析和计算某一磁路系统时常常模仿电路的表示形式将它表示成等值磁路图。图中引用电路中代表电动势和电阻的符号来代表磁通势和磁阻。

图6-4a所示为一拍合式电磁铁的磁系统。它的导磁磁路由插入线圈的铁心、L形的铁轭和能绕轴转动的吸片（也称“衔铁”）所组成。线圈通电后，绝大部分磁通将通过铁心、铁轭、吸片以及吸片与铁心端面间的空气隙δ₁（称为主工作气隙）而构成闭合磁路。该磁通对吸片产生吸力，因而称为主磁通Φ_δ，主磁通的平均磁力线如图中虚线所示，该磁系统的等值磁路图如图6-4b所示。

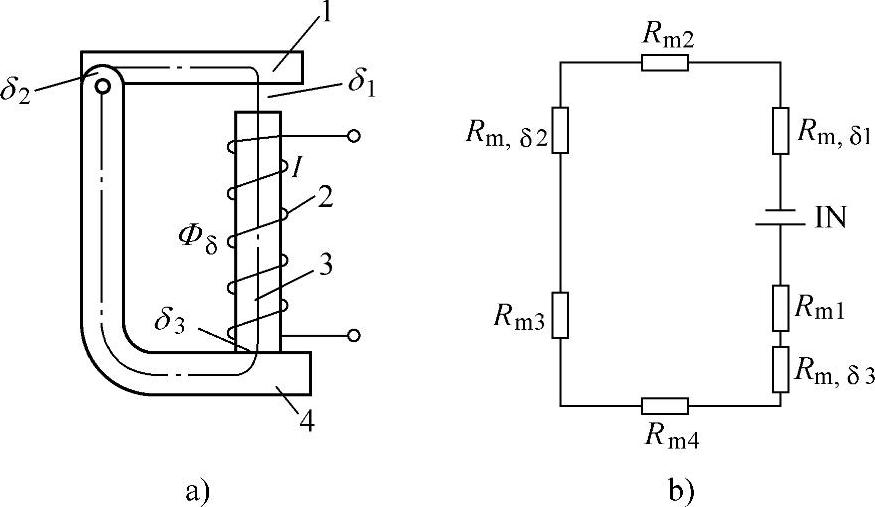
图6-4 拍合式磁系统及其等值磁路图

a）磁路 b）等值磁路 1—吸片 2—线圈 3—铁心 4—铁轭 IN—线圈磁通势（长的一横代表N极，短的一横代表S极） R_m，δ₁—主工作气隙的磁阻 R_m，δ₂—转轴配合处的气隙磁阻 R_m，δ₃—铁心和铁轭配合处的气隙磁阻 R_m1—铁心磁阻 R_m2—吸片磁阻 R_m3及R_m4—铁轭磁阻

（2）磁路的克希荷夫二定律 计算具有分支的多回路电路需运用电路的克希荷夫（Kirchhoff）二定律，同样在计算复杂磁路时也可应用类似的磁路克希荷夫二定律。磁路克希荷夫二定律实质上就是磁通连续性原理和安培环路定律在磁路中的应用。与电路相似，把同一磁通通过的路径称为“支路”，而把三条或三条以上的支路会聚处称为“节点”。

磁通连续性原理指出，磁场中穿出（或穿入）一个封闭曲面的磁通总和恒为零。如果我们把封闭曲面取在磁路的节点处，如图6-5所示，显然应有

∑Φ=0 （6-15）

即汇聚在任一节点上的磁通的代数和恒等于零，这就是磁路的克希荷夫第一定律。

同样，根据安培环路定律也可以得到相应的磁路克希荷夫第二定律，即对于任一闭合磁回路，沿某一环绕方向，其磁压降的代数和恒等于该回路中磁通势的代数和，即

∑IN=∑U_m=∑ΦR_m （6-16）

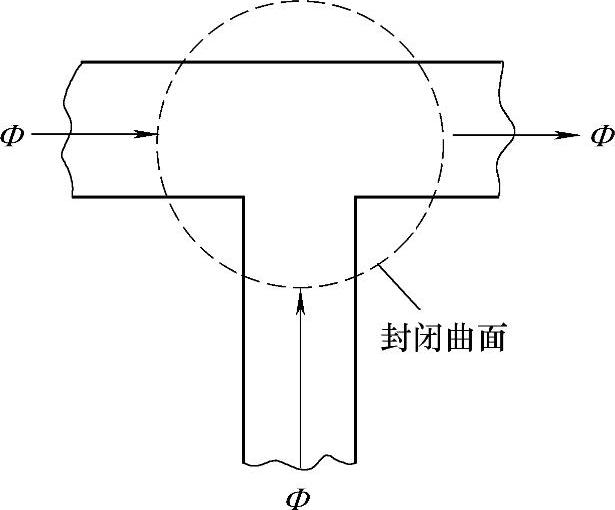
图6-5 磁路分叉处

如果磁路各分段中的B（或H）可假定为常数，并且其方向与环路方面一致，则磁路克希荷夫第二定律也可表示为

∑IN=∑Hl （6-17）

磁路克希荷夫二定律对于任何形式的磁路都是普遍适用的，也就是说，不论导磁体的磁阻是线性（即_μ为常性）还是非线性（即μ不是常数），也不论考虑还是不考虑漏磁现象，磁路克希荷夫二定律都是适用的。