机器人运动学基础概述

服务机器人的执行机构是应用在复杂作业环境空间中的综合体。而且，通常情况下，它本身也必须保证作为一个统一的整体在工作过程中运动。因此，需要一种简便灵活的数学方法，用来描述单一刚体的位移、速度和加速度等参数，以便很好地解决服务机器人在运动学上的问题。而这种数学方法不一定是统一形式的，不同的研究者可能会采用不同的方法。本书所采用的是矩阵法，用以描述服务机器人的运动学和动力学问题。基于矩阵的数学描述法的基本思想是将矩阵的运算与服务机器人的运动、变换和映射结合起来，利用四阶的方阵实现三维空间中点的齐次坐标转换。

在研究服务机器人运动的过程中，不仅需要考虑机器人本身的运动，而且要考虑工作环境中各个作业之间，以及作业与服务机器人之间的关系。这些关系的表示相对比较复杂，将采用齐次坐标及其矩阵变换来表示。因为齐次坐标的矩阵变换数学建模能力比较突出，它不但可以表示机器人的运动学问题，而且能够表达服务机器人的控制算法、计算机图形学和计算机视觉等问题，所以，研究者特别青睐这种数学表示方法。

1.服务机器人的位置描述和坐标变换

首先需要建立一个空间坐标系，用以描述空间中点的位置。接着，在该坐标空间中，使用一个3×1的位置向量来确定空间内的任意一个点，该向量被称为“位置矢量”。在确定了物体的位置之后，还需要将物体的姿态表示出来。同样的，使用一个3×3矩阵来表示物体的姿态，该矩阵处于固接在对应物体的坐标系中。另外，还需要依据约束条件给出焊接机器人的旋转变换矩阵，该矩阵表示以对应坐标轴进行旋转θ角的变换。物体在坐标空间中的位姿（位置与姿态）可以由以上给出的位置矢量和姿态矩阵共同来表示。

1）位置的描述

如果给定了空间坐标系，则该空间内点的位置就可以由一个三维的矢量来描述。例如：给定直角坐标系{}A，该空间中点q的位置可用一个3×1的列向量Aq表示。

式（3.1）中，左下标A代表点q所处的参考坐标系为{A}。qx，qy，qz分别表示点q在{A}中的3个坐标分量值。则将Aq称为点q的位置矢量（见图3-5）。

图3-5　点的位置表示示意图

2）方位的描述

要全面研究服务机器人的操作与运动，既需要知道空间中物体点的位置，又需要了解代表物体方位（orientation）的矩阵。通常情况下，使用固接在物体上的坐标系来描述物体的具体方位。假设，在规定的空间中有一个刚体G，再设定一个直角坐标系{G}与该刚体相固接。

使用坐标系{G}的三个单位向量xG，yG，zG相对于参考坐标系{A}的位置来表示刚体G的方位，如下所示：

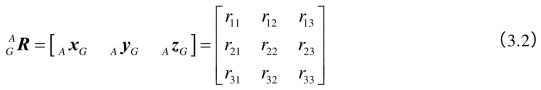
式（3.2）中，称为旋转矩阵。有9个参数，它们分别表示了矢量xG，yG，zG对应于{A}中坐标轴的方向余弦值。

可以证明，旋转矩阵是一个正交的矩阵。并且能够满足如下条件：

进一步可得，刚体相对参考系的x轴、y轴或z轴，做ω角度的旋转变换，其对应的旋转变换可以描述为如下形式：

在式（3.4）～（3.6）中，s代表sin，c代表cos。

如图3-6所示，G代表物体；{G}表示与物体对应的坐标系，并且能够进行以坐标系{A}为参考的旋转运动。

图3-6　物体的方位表示示意图

3）位姿的描述

在确定了物体的方位与位置之后，就能够考虑描述物体在坐标空间中的位姿（位置和姿态）。同样的，在表示物体G的位姿之前，首先需要将物体G放在与其相对应的坐标系{G}中，并且，一般将物体G的质心作为{G}的坐标原点。

坐标系{G}原点的位置由位置矢量标示，坐标系{G}坐标轴的方位由旋转矩阵来表示。所以，使用坐标系{G}来描述刚体G的位姿，其计算公式如下：

上式中，若位姿{G}仅仅表示刚体的位置，则旋转矩阵(单位矩阵)。

同理，若位姿{G}仅仅表示刚体的方位，式（3.7）中的位置矢量。(www.xing528.com)

4）服务机器人的坐标变换

要知道，空间中的点q在不同坐标系中有不同的位姿参数。需要找到一种数学模型，来描述点q从一个坐标系到另一个坐标系的变换关系。

在通常的情形下，坐标系{G}与参考系{A}的原点不会在同一位置，它们的方位也不会相同。

因此，使用位置矢量和旋转矩阵来共同描述{G}相对于{A}的位姿。

如下图3-7所示。

图3-7　空间中物体复合变换的示意图

在空间中，一般都同时存在着物体的平移变换和旋转变换。点q在{A}和{G}中的位置分别由Aq和Gq来描述，它们具有如下关系：

a）齐次坐标变换

式（3.8）是非齐次的，然而，能够使用等价的齐次变换将其表示出来，形式如下：

需要说明的是，式（3.9）中最左边和最右边的式子均可称为点的齐次坐标，依旧将它们记为Aq和Gq。则，与式（3.9）相等价的矩阵可表示为

式（3.10）中，齐次坐标Aq和Gq均加入了第4个元素1，是4×1的列向量。齐次变换矩阵的表达形式如下：

由矩阵的形式，能够看出：变化矩阵代表了刚体进行平移变换和旋转变换所产生的综合效果。式（3.9）和式（3.8）的意义是等价的。

b）平移齐次坐标的变换

假设：i，j，k分别为坐标系中x轴，y轴，z轴上的单位向量，则矢量li+mj+nk可以表示该坐标空间中的某个点。所以，平移齐次变换的关系矩阵可以表示为如下形式：

式（3.12）中，Ts代表平移变换关系。

例如：已知向量u=[x,y,z,γ]T，对其进行平移变换后所得的结果由向量ζ表示。向量ζ的计算公式如下：

可把平移齐次坐标变换看作是向量与向量li+mj+nk相加之和。

c）旋转齐次坐标的变换

若物体对应于参考系{A}的坐标轴x、y或z，作角度为ω的旋转运动，则分别可得如下表示旋转变换关系的矩阵：

式（3.14）～（3.16）中，Rt代表旋转变换关系。