国外动力煤干燥无灰基成分的理论绝热燃烧温度分布规律

根据表2-5～表2-8 的数据和第3.3 节的计算方法，国外动力煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）计算结果见表4-34～表4-37。

国外动力煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）分布规律直观地反映在图4-19、图4-20 中，其中的多项式拟合函数参数见表4-38。

表4-34 国外无烟煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）计算结果 ℃

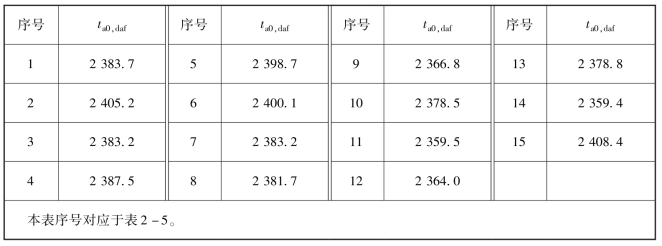
表4-35 国外贫煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）计算结果 ℃

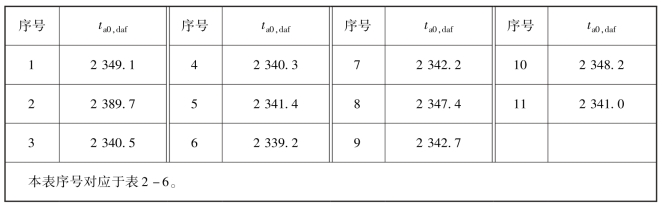
表4-36 国外烟煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）计算结果 ℃

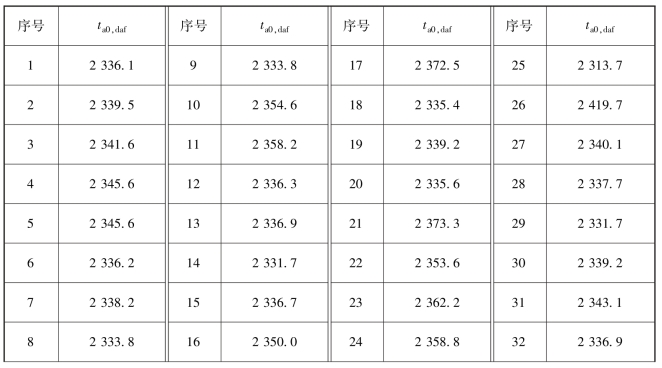
续表

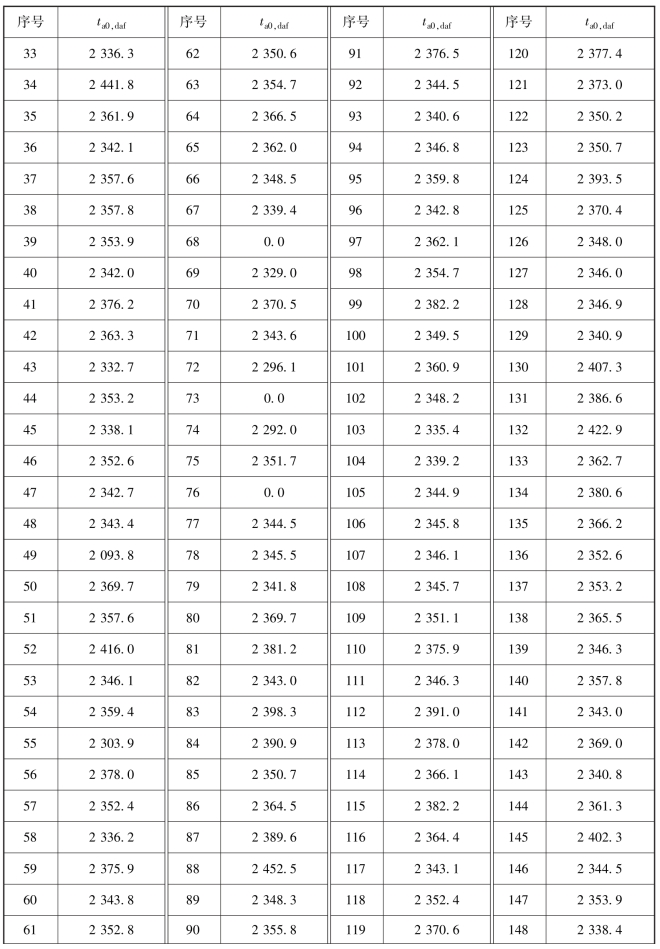
续表

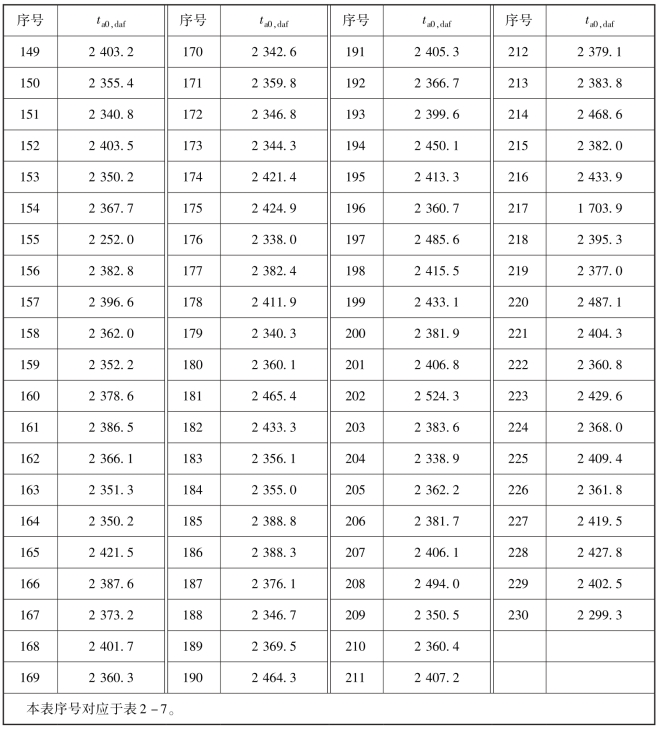
表4-37 国外褐煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）计算结果 ℃(www.xing528.com)

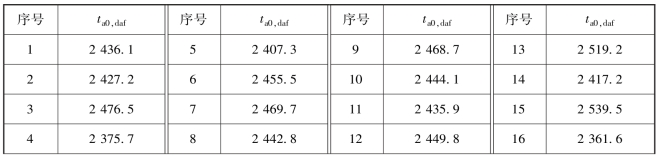
续表

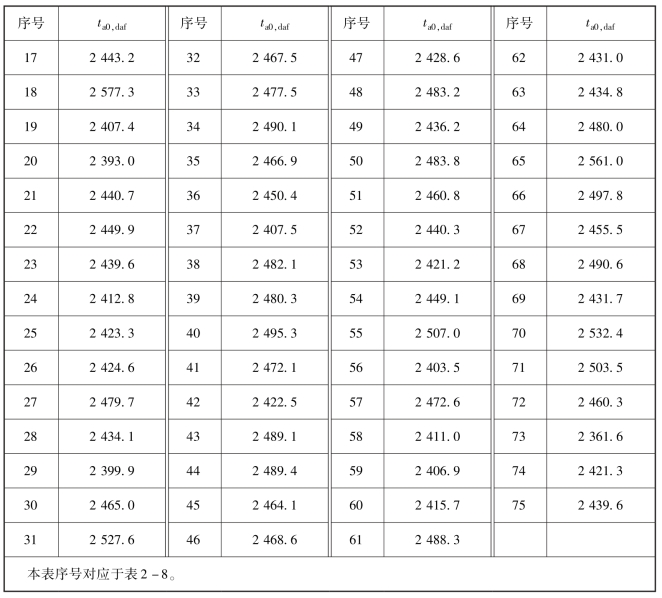
由图4-19 拟合曲线可知：随着Vdaf的提高，国外动力煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）先缓慢降低，后快速提高。Vdaf≤21%时，也就是在无烟煤、贫煤范围以及少量挥发分低的烟煤范围内，ta0，daf从2 362.6℃降低到2 351.6℃，降低的速度随着Vdaf的提高逐渐降低到0；Vdaf＞ 21%时，ta0，daf从2 351.6℃提高到2 536.2℃，提高的速度随着Vdaf的提高逐渐加快。

由图4-20 拟合曲线可知：随着Qdaf，net的提高，国外动力煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）单调降低，从2 548℃降低到2 322℃。

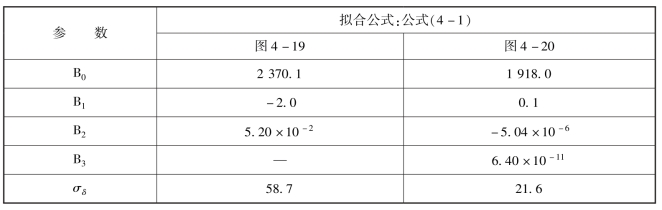
比较图4-19、图4-20、表4-38 数据可知：国外动力煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）的数据与多项式拟合函数之间存在一定的分散度。ta0，daf与Vdaf的函数关系中，数据分散度较大，残差标准差为58.7；ta0，daf与Qdaf，net的函数关系中，数据分散度较小，残差标准差为21.6。在图4-19、图4-20 中可以明显观察到上述数据分布特点。

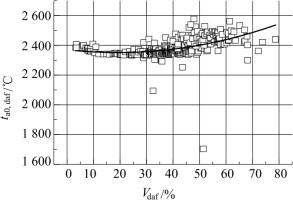
图4-19 国外动力煤干燥无灰基成分的理论绝热燃烧温度与Vdaf的关系

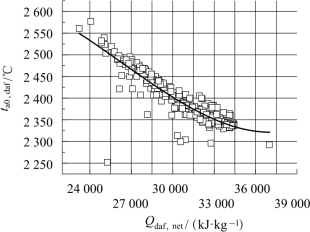
图4-20 国外动力煤干燥无灰基成分的理论绝热燃烧温度与Qdaf，net的关系

比较图4-17～图4-20可知：虽然国外动力煤理论绝热燃烧温度（ta0）的分布规律类似于工程绝热燃烧温度（taE）的分布规律，但由于过量空气系数降低为1.0，因此烟气量降低，烟气焓提高，同一种煤的ta0，daf＞ta0。

表4-38 国外动力煤干燥无灰基成分的理论绝热燃烧温度（ta0，daf）与Vdaf、Qdaf，net多项式拟合函数参数