机械特性：2.6.3kf>1的影响

k_f＞1时的一个重要特点是，U_X=U_N=const。即一般情况下，电动机不可能在超过额定电压的情况下运行。与k_f<1时一样，仍通过临界点的坐标来进行观察。

1.临界转矩 将k_u=1代入式（2-17），得

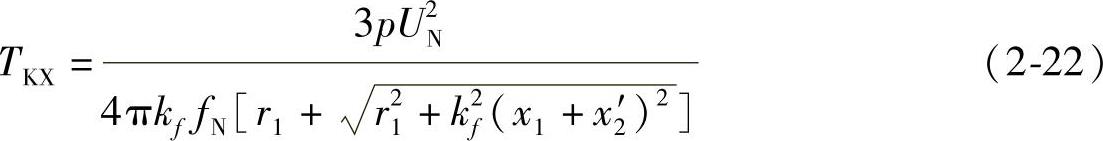
因为k_f≥1时，k_f²（x+x₂′）＞＞r₁，所以如果略去r₁不计，式（2-22）可简化为

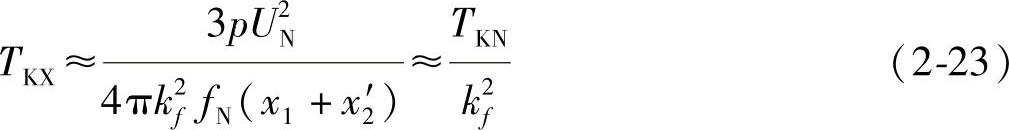
式中 T_KN———k_f=1（f_X=f_N）时的临界转矩。

式（2-23）表明，临界转矩的大小与k_f²成反比。

这是近似计算的结果。实际上，根据变频器生产厂商提供的资料，临界转矩大致可按下式计算：

T_KX=T_KN/k_f^1.4 （2-24）

2.临界转差率 由于s_KX和s_K′_X均和电压无关（和k_u如何变化无关），故其大小仍分别由式（1-40）和式（2-18）决定。如果忽略r₁不计，则

s_K′_X≈r₂′/（x₁+x₂′）≈s_KN而临界转差Δn_KX的大小是(www.xing528.com)

Δn_KX=s_K′_Xn_0N≈Δn_KN以上各式中，凡下足标中带“X”者均为f₁=f_X时的值，带“N”者均为f₁=f_N时的值。

可见临界转差几乎不变。

今将某电动机在k_f>1时，临界点坐标的计算结果列于表2-3中。

表2-3 k_f>1时的临界点

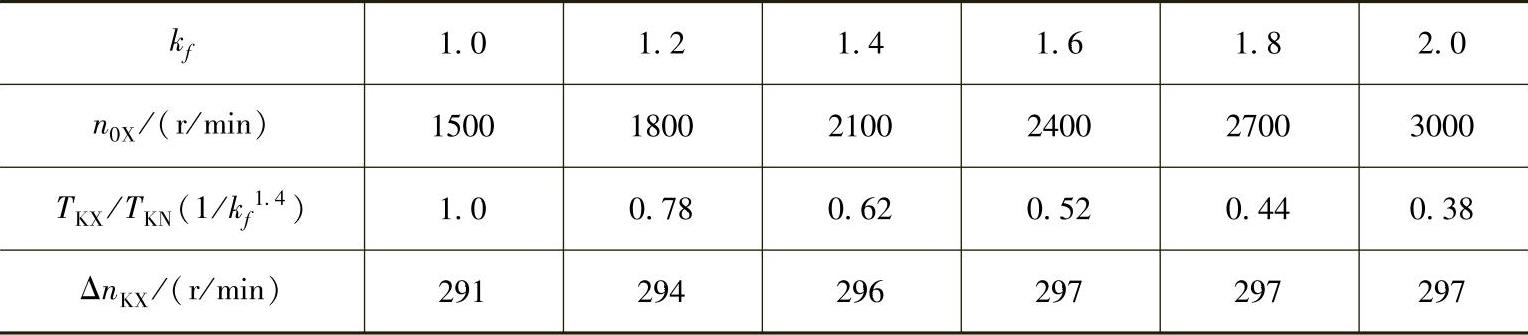
由表2-3所得数据作出的机械特性曲线如图2-19所示。由图可知

（1）f_X升高时，T_KX近乎按（1/k_f^1.4）的规律减小。

（2）临界转差Δn_KX变化很小，但因临界转矩减小很多，故机械特性的倾斜度加大，工作区的机械特性略为变软。

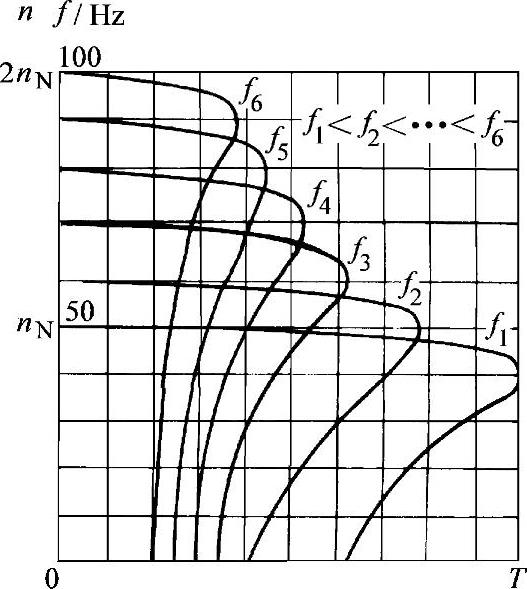
图2-19 k_f>1时的机械特性