机械特性：当ku=kf＜1时的优化方案

异步电动机机械特性的大致形状主要通过临界点的坐标来观察。

1.临界转矩 详细的定量分析不属本书的介绍范围。这里，只是根据两种极端情况，大概地分析其变化趋势。

（1）当k_u=k_f→1时，有

k_f（x₁+x₂′）＞＞r₁如果忽略r₁不计，则

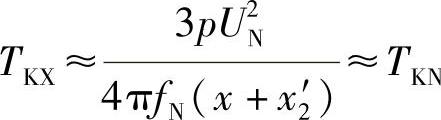
即当k_u=k_f趋近于1时，T_KX的大小趋近于T_KN值。

（2）当k_u=k_f→0时，有

k_f（x₁+x₂′）＜＜r₁

如果忽略k_f（x₁+x₂′）不计，则有

即当k_u=k_f趋近于0时，T_KX的大小趋近于与k_u成正比。需要说明的是，因为在k_f=1时，x₁+x₂′>>r₁，所以只有当k_f＜0.1时，k_f（x₁+x₂′）＜＜r₁才是成立的。

综合上述两种极端情况可以看出，从k_f=1→k_f=0的过程中，T_KX是逐渐减小的。开始时减小得比较慢，当k_f很小时，T_KX减小得较快。

2.临界转差 由式（2-18）可知：

（1）k_f→1时，如忽略r₁不计，则

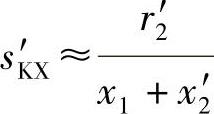
所以，s_K′_X和Δn_X几乎不变。

（2）k_f→0时，如忽略k_f（x₁+x₂′）不计，则

s_K′_X≈k_fr₂′/r₁∝k_f

所以，s_K′_X和Δn_X都随k_f而减小。

今将某一电动机的计算结果列于表2-2中。(www.xing528.com)

表2-2 k_u=k_f＜1时的临界点坐标

由表2-2的数据作出的k_u=k_f<1时的机械特性曲线簇如图2-18所示。由图可知：

（1）f_X不同时，在相同转矩时的速度降Δn_X变化很小，所以工作区的机械特性曲线大致是平行的，保持了较硬的机械特性。

（2）随着f_X的下降，临界转矩T_KX逐渐减小，电动机的带负载能力也随之下降。

3.T_KX减小的物理意义如2.4.2节所述，用k_u=k_f来维持电动机的主磁通不变（Φ_M=const）的方法，是以U₁近似地代替E₁（认为U₁≈E₁）的结果。这种近似代替，是以忽略阻抗压降ΔU₁为代价的。

问题是，当f₁=f_X下降，U₁=U_X也按比例下降时，ΔU₁=ΔU_X是否也按比例下降？近似式U_X≈E_X（E_X为f₁=f_X时的反电动势）能否始终成立？

图2-18 k_u=k_f<1时的机械特性

当f₁=f_X时，阻抗压降是

式中 ΔU_X———f₁=f_X时的阻抗压降；

ΔU_r———定子绕组的电阻压降；

ΔU_LX———f₁=f_X时，定子绕组的漏抗压降。

f_X下降时，漏抗压降ΔU_LX=k_fI₁x₁也随着下降，但电阻压降ΔU_r=I₁r₁却与f_X无关。因此，当U_X随着f_X下降时，ΔU_X在U_X中所占的比例逐渐增大，而E_X所占的比例则逐渐减小，U_X≈E_X的误差越来越大。当U_X降得很低时，式（2-6）的关系已不能成立，而成为

式（2-21）表明，在保持U_X/f_X=const的情况下，随着f_X的下降，比值E_X/f_X也在减小，从而Φ_M也减小。由式（1-25）可知，Φ_M的减小，必将导致电磁转矩的减小。

对以上分析，可归结如下：

k_u=k_f↓→ΔU_X/U_X↑→E_X/U_X↓→Φ_M↓→T_KX↓