传感器的动态特性及影响因素分析

传感器的动态特性是指其输出量对随时间变化的输入量的响应特性。当被测量随时间变化，是时间的函数时，则传感器的输出量也是时间的函数，其间的关系要用动态特性来表示。一个动态特性好的传感器，其输出量将再现输入量的变化规律，即具有相同的时间函数。实际上除了具有理想的比例特性外，输出信号将不会与输入信号具有相同的时间函数，这种输出与输入间的差异就是所谓的动态误差。

为了说明传感器的动态特性，下面简要介绍动态测温的问题。在被测温度随时间变化或传感器突然插入被测介质中，以及传感器以扫描方式测量某温度场的温度分布等情况下，都存在动态测温问题。例如，把一支热电偶从温度为t0℃环境中迅速插入一个温度为t℃的恒温水槽中（插入时间忽略不计），这时热电偶测量的介质温度从t0突然上升到t，而热电偶反映出来的温度从t0℃变化到t℃有一个过渡过程，其间反映出来的温度与介质温度的差值就称为动态误差，如图1-5所示。

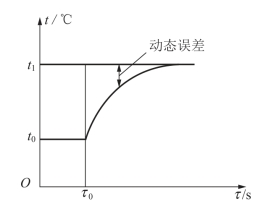
图1-5　动态测温

造成热电偶的输出波形失真和产生动态误差的原因，是因为温度传感器有热惯性（由传感器的比热容和质量大小决定）和传热热阻，使得在动态测温时传感器输出总是滞后于被测介质的温度变化。如带有套管的热电偶的热惯性要比裸热电偶大得多。这种热惯性是热电偶固有的，它决定了热电偶测量快速温度变化时会产生动态误差。动态特性除了与传感器的固有因素有关之外，还与传感器输入量的变化形式有关。也就是说，在研究传感器的动态特性时，通常是根据不同输入变化规律来考察传感器的响应的。

虽然传感器的种类和形式很多，但它们一般可以简化为一阶或二阶系统（高阶可以分解成若干个低阶环节），因此一阶和二阶传感器是最基本的。传感器的输入量随时间变化的规律是各种各样的，下面在对传感器动态特性进行分析时，采用最典型、最简单、易实现的正弦信号和阶跃信号作为标准输入信号。对于正弦输入信号，传感器的响应称为频率响应或稳态响应；对于阶跃输入信号，则称为传感器的阶跃响应或瞬态响应。

1.瞬态响应特性

传感器的瞬态响应是时间响应。在研究传感器的动态特性时，有时需要在时域中对传感器的响应和过渡过程进行分析。这种分析方法是时域分析法，传感器对所加激励信号的响应称为瞬态响应。常用激励信号有阶跃函数、斜坡函数、脉冲函数等。下面以传感器的单位阶跃响应来评价传感器的动态性能指标。

（1）一阶传感器的单位阶跃响应

一阶传感器的单位阶跃响应的通式为

式中，x（t）、y（t）分别为传感器的输入量和输出量，均是时间的函数。表征传感器的时间常数，具有时间“秒”的量纲。

一阶传感器的传递函数：

对初始状态为零的传感器，当输入一个单位阶跃信号时，由于

则X（s）＝1s，传感器输出的拉氏变换为

一阶传感器的单位阶跃响应为

相应的响应曲线如图1-6所示。由图可见，传感器存在惯性，它的输出不能立即复现输入信号，而是从零开始，按指数规律上升，最终达到稳态值。理论上传感器的响应只在t→∞时才达到稳态值，但实际上当t＝4τ时其输出达到稳态值的98.2％，可以认为已达到稳态。τ越小，响应曲线越接近输入阶跃曲线，因此，τ值是一阶传感器的重要性能参数。

图1-6　一阶传感器单位阶跃响应

（2）二阶传感器的单位阶跃响应

二阶传感器的单位阶跃响应的通式为

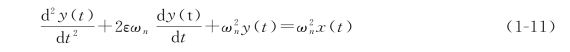
式中，ωn为传感器的固有频率；ε为传感器的阻尼比。

二阶传感器的传递函数：

传感器输出的拉氏变换：

(www.xing528.com)

二阶传感器对阶跃信号的响应在很大程度上取决于阻尼比ε和固有频率ωn。固有频率ωn由传感器的主要结构参数所决定，ωn越高，传感器的响应越快。当ωn为常数时，传感器的响应取决于ε。如图1-7所示为二阶传感器的单位阶跃响应曲线。阻尼比ε直接影响超调量和振荡次数。当ε＝0时，为临界阻尼，超调量为100％，产生等幅振荡，达不到稳态；当ε＞1时，为过阻尼，无超调也无振荡，但达到稳态所需时间较长；当ε＜1时，为欠阻尼，衰减振荡，达到稳态值所需时间随ε的减小而增长；当ε＝1时，响应时间最短。但实际使用中常按欠阻尼调整，ε＝0.7～0.8为最好。

图1-7　二阶传感器单位阶跃响应

（3）瞬态响应特性指标

①时间常数τ。一阶传感器的时间常数τ越小，响应速度越快。

②延时时间。传感器输出达到稳态值的50％所需时间。

③上升时间。传感器输出达到稳态值的90％所需时间。

④超调量。传感器输出超过稳态值的最大值。

2.频率响应特性

传感器对正弦输入信号的响应特性，称为频率响应特性。频率响应法是从传感器的频率特性出发研究传感器的动态特性。

（1）一阶传感器的频率响应

将一阶传感器的传递函数中的s用jω代替，可得频率响应特性的表达式，即

幅频特性：

相频特性：

从式（1-15）、式（1-16）和图1-8看出，时间常数τ越小，频率响应特性越好。当ωτ＜＜1时，A（ω）≈1，Φ（ω）≈0，表明传感器的输出与输入为线性关系，且相位差也很小，输出y（t）比较真实地反映输入x（t）的变化规律。因此，减小τ可改善传感器的频率特性。

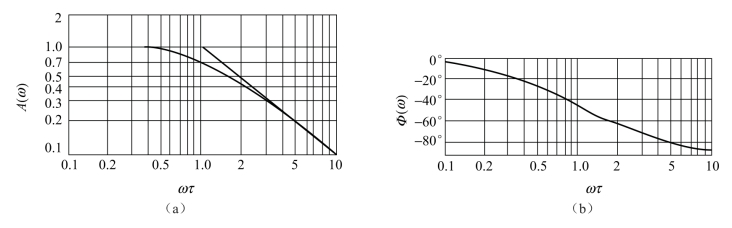
图1-8　一阶传感器的频率响应特性

（2）二阶传感器的频率响应

二阶传感器的频率响应特性表达式、幅频特性、相频特性分别为

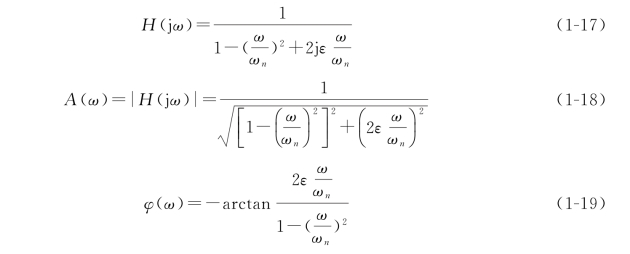
如图1-9所示为二阶传感器的频率响应特性曲线。从式（1-18）、式（1-19）和图1-9可见，二阶传感器的频率响应特性的好坏主要取决于传感器的固有频率ωn和阻尼比ε。当ε＜1，ωn＞＞ω时，A（ω）≈1，Φ（ω）很小，此时，传感器的输出y（t）再现了输入x（t）的波形。通常固有频率ωn至少应大于被测信号频率ω的3～5倍，即ωn≥（3～5）ω。

为了减小动态误差和扩大频率响应范围，一般是提高传感器固有频率ωn。而ωn与传感器运动部件质量m、弹性敏感元件的刚度k有关，即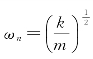。增大刚度k和减小质量m可提高固有频率，但刚度k增加，会使传感器的灵敏度降低。所以在实际中，应综合各种因素来确定传感器的各个特征参数。

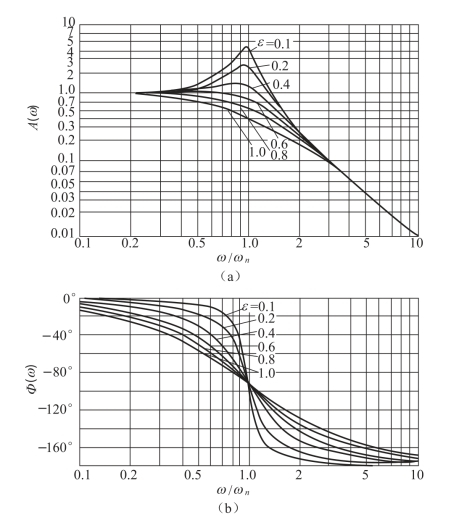
图1-9　二阶传感器频率响应特征

（3）频率响应特性指标

①频带。传感器增益保持在一定值内的频率范围称为传感器频带或通频带，对应有上、下截止频率。

②时间常数τ。用时间常数τ来表征一阶传感器的动态特性。τ越小，频带越宽。

③固有频率ωn。二阶传感器的固有频率ωn表征了其动态特性。