试验结果与分析深度解析

7.5.2.1　动态应力-应变关系

与研究材料准静态力学行为不同，在研究材料高应变率下的动态力学行为时，必须计及两类基本的动力学效应：结构惯性效应（也称为应力波效应）和材料应变率效应。前者导致了各种应力波传播和其他形式的结构动力学研究；后者导致了各种类型的、应变率相关的本构关系和破坏准则的研究［299，194］。在中应变率SHPB试验中，试件厚度通常远小于脉冲宽度，试件内部沿长度方向的应力/应变分布将很快趋于均匀，从而可以忽略试件的应力波效应。SHPB试验采取将应力波效应和应变率效应解耦的方法，其是目前使用最为广泛的材料应变率效应研究方法。为了更好地反映材料惯性效应和应变率效应的耦合，本节采用拉氏分析方法，通过波传播法来研究材料高压、高应变率下的本构关系。

拉氏分析［194，305-307］通过在材料内部不同位置处埋入传感器，得到一组应力或粒子速度的变化曲线，通过普适守恒方程计算得到完整的流场信息。该方法不依赖事先的本构假定，得到的流场时-空分布曲线是真实过程的写照，可反映材料在试验过程中的动态响应行为历程。在忽略热传导、体积力等的假设条件下，一维应变平面波拉格朗日坐标下的普适守恒方程为：

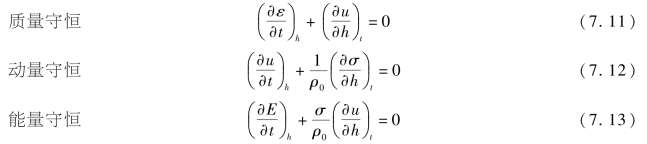
式中，ρ0为初始密度；ε为应变；u为粒子速度；t为时间；σ为应力；E为比内能；h为拉格朗日位置坐标。采用路径线法对上述偏微分方程组进行求解，如图7.32所示，路径线实际上就是一条人为构筑的连接各波形的曲线。多条相互间隔的路径线与量计线（锰铜压阻传感器记录的σ-t波形）联系在一起，构成一个逼近实际流场曲面的网状框架，然后依赖普适的守恒方程数值模拟出流场中的其他力学量。

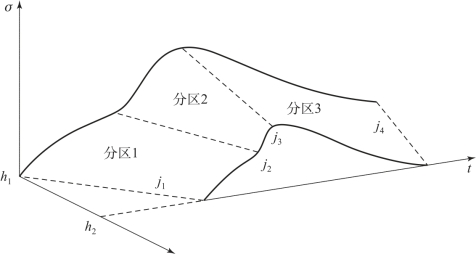
图7.32　路径线与量计线构成的σ-h-t空间波形示意图

如图7.32所示，因平板撞击试验中，在三层靶板中嵌埋两个锰铜压阻传感器，故量计线序号i从1到2，在每条量计线上取相等数量的节点，序号从1到N，节点（i，j）上的应力为σi，j。在每条量计线上等时间间隔选取节点，不同量计线上对应的时间单元不一定相同。将各量计线上对应节点用一条光滑曲线连接起来就是路径线。每条量计线上有N个节点，就能连接得到N条路径线，依靠这些路径线就可以把整个流场的信息联系起来。沿量计线对式（7.11）～式（7.13）在短时间间隔（t1，t2）内积分，于是可以得到：

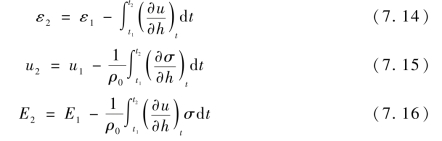
由于一般情况下求出等时线是十分困难的，故在等时状况下求解和难度较大，并且给计算带来不必要的误差，因此，一般采用路径线技术来求解。路径线技术实际上是一种数学变换方法，其目的在于将沿等时线的积分转换成沿路径线的积分。设一力学量φ在h-t直角坐标系中表示为φ（h，t），在h-t坐标平面内引入另一新的路径线坐标j，在此平面内，j与h构成一个新的坐标系，新旧坐标系的变换关系为：

由式（7.17）可知，当h一定时，j和t有一定的对应关系，因此，j可以作为自然时间坐标。用j代替t，则曲面σ（h，t）、u（h，t）等均可以变换成曲面σ（h，j）、u（h，j）等，这样通过路径线就可以将沿等时线的积分转换成沿路径线和量计线的微分。力学量φ的坐标变换如下：

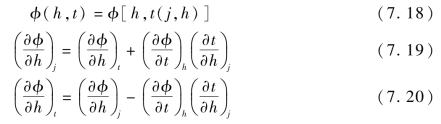
如果已知流场σ-t，把上式代入式（7.14）～式（7.16），利用梯形公式对方程进行积分。沿着第i条量计线在时间单元（j，j＋1）内相应的差分方程为：

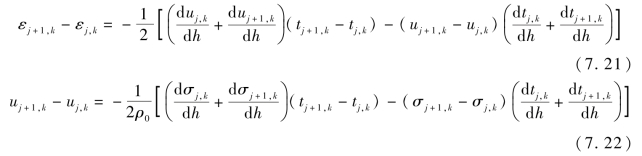
用Matlab对上述差分方程进行编程［295］。为了表示波传播的特征，根据所测量计波形特征，将量计线分成若干区。如图7.33（a）所示，根据锰铜压阻传感器实测压力-时间信号，将量计线分成加载区、平台段和卸载区三个部分［69］，并采用Savitzky-Golay滤波器对数据流进行平滑除噪处理，滤波后的应力-时间信号如图7.33（b）所示。由应力场通过式（7.22）可逐步求解速度场（图7.33（c）），然后由速度场可逐步求解应变（图7.33（d））和比内能（图7.33（e））等。

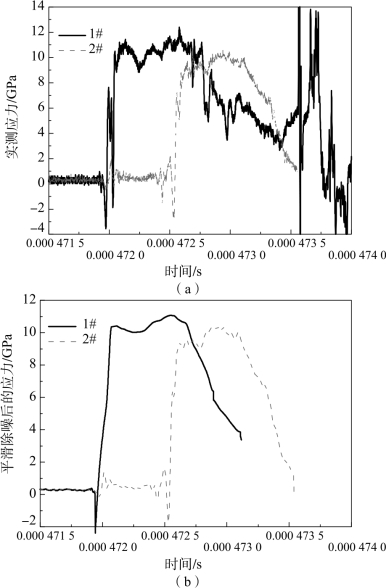
图7.33　623 m/s撞击速度下35CrMnSiA钢各力学量的时-空分布特性

（a）实测应力-时间曲线；（b）平滑除噪后的应力-时间曲线

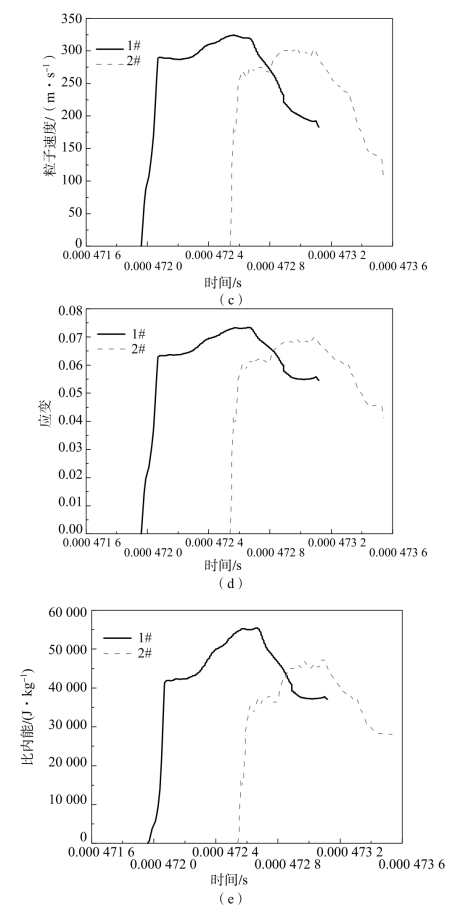
图7.33　623 m/s撞击速度下35CrMnSiA钢各力学量的时-空分布特性（续）

（c）粒子速度-时间曲线；（d）应变-时间曲线；（e）比内能-时间曲线

图7.33　623 m/s撞击速度下35CrMnSiA钢各力学量的时-空分布特性（续）

（f）应力-应变曲线

高压高应变率下的35CrMnSiA钢的应力-应变曲线如图7.34所示。由图7.34可见，高压高应变率下35CrMnSiA钢具有如下动态响应特性：

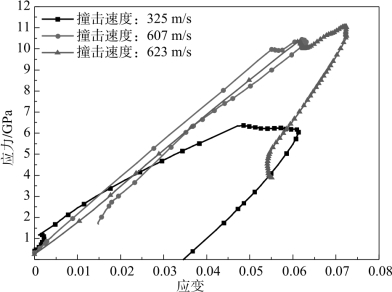
图7.34　高压高应变率下35CrMnSiA钢的应力-应变曲线

（1）应变率相关性

由图7.34可以发现，35CrMnSiA钢的应力峰值随着撞击速度的增加而增大，也就是抗压强度随应变率的增加而递增，表现出明显的应变率敏感性。

（2）应力-应变关系总体呈滞徊型

同一加载速度下，同一测点处的应力-应变加、卸载段曲线并不重合，即卸载时应变不能完全恢复；加载初始段斜率较大，在接近峰值时曲线弯向应变轴，斜率下降，这时较小的应力增量就会引起较大的应变增量。当卸载到某一压应力时，其应变较加载到同一应力时大；当应力卸载到零时，还有较大的残余应变。

（3）材料的流变特性

材料在加载到强度极限后，存在一个应变软化过程，这一由“应变强化为主”到“应变软化为主”的“本构失稳”现象是与材料固有的应变强化机制和损伤演化引起的软化机制共存又相互竞争的过程密切相关的。一方面，应变率强化效应可以和应变硬化效应一起来抵制材料软化破坏，以阻止本构失稳的发生；另一方面，伴随着变形增大、应变率提高和固态相变，材料微裂纹也增多，必定削弱材料的抗变形能力，导致材料的软化破坏［308］。

7.5.2.2　Hugoniot关系

通过对DISAR探针记录的频域信号进行傅里叶变换，得到不同撞击速度下靶板自由面粒子速度历史曲线，如图7.35所示。在607 m/s的撞击速度下，35CrMnSiA钢靶板内一维应变平面波呈现由弹性前驱波E和第一塑性冲击波P1构成的双波结构。当靶板内应力超过HEL（Hugoniot弹性极限）时，材料由弹性状态进入弹塑性Hugoniot状态。Hugoniot弹性极限可视为一维应变状态下材料的屈服强度。当撞击速度达到1 240 m/s时，一维应变平面波呈现三波结构，走在最前面的是弹性前驱波E，以材料的一维应变弹性纵波波速Ce传播，波幅等于材料的Hugoniot弹性极限；跟在弹性前驱波E后面的是两个塑性冲击波P1和P2，第一塑性冲击波P1将材料冲击压缩到相变时的压力pc，第二塑性冲击波P2将材料由相变压力冲击压缩至最终状态。当撞击速度增加到1 733 m/s时，由于第二塑性波P2的波速已加快到超过第一塑性冲击波P1的波速，从而形成了一个新的传播速度更快的塑性冲击波，故此时仅观测到由弹性前驱波E和第二塑性波P2构成的双波结构［309，310］。综上所述，当撞击速度高于1 240 m/s时，35CrMnSiA钢发生了相变。

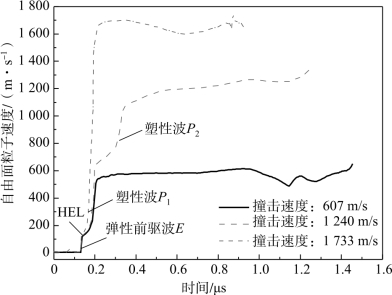
图7.35　35CrMnSiA钢自由面粒子速度历史曲线

锰铜压阻传感器测试得到的典型试验测试信号如图7.36所示。一维应变平面波剖面由冲击波波阵面（上升沿）、恒定应力平台（Hugoniot状态）及弥散卸载波（下降沿）三部分组成，未能观察到明显的弹性波与塑性波分界点。通过测量冲击波波阵面到达两压阻传感器时的时间差Δt（即两传感器所测冲击波上升沿的时间间隔），可计算得到靶板中的冲击波速度D，不同撞击速度下测试得到的试验结果列于表7.8中。

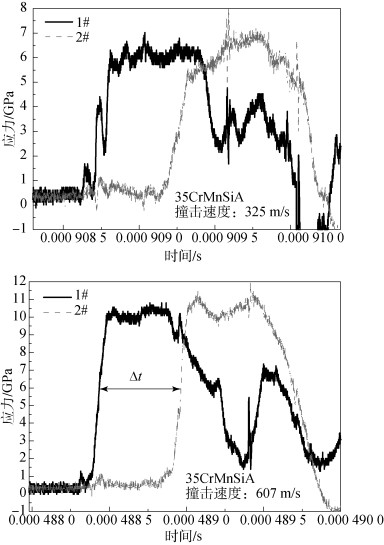
图7.36　锰铜压阻传感器试验测试信号

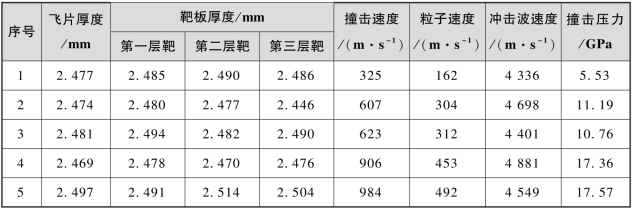
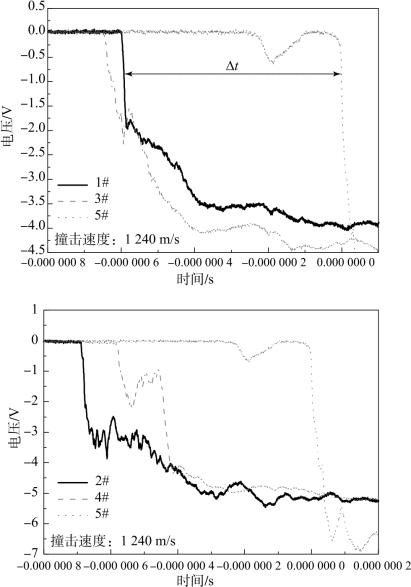
光纤探针测试得到的典型试验信号如图7.37所示。通过测量冲击波波阵面到达光纤探针的时间差Δt（即靶板撞击端面和背面处光纤探针所测信号下降沿的时间间隔），可计算得到靶板中的冲击波速度D。为了减小探针端面与靶板撞击端面的非共面误差，分别取1＃和3＃探针响应时刻的平均值与2＃和4＃探针响应时刻的平均值计算冲击波速度，再取二者平均值作为实测冲击波速度值。不同撞击速度下测试得到的试验结果列于表7.9中。为了讨论锰铜压阻传感器和光纤探针冲击波速度测量结果的一致性问题，对飞片撞击速度为607 m/s的试验工况分别用上述两种传感器进行冲击波速度测量，试验结果见表7.8和表7.9。两种测试方法测得冲击波速度分别为4 698 m/s和4 797 m/s，相对误差仅为2.11%，结果呈现较好的一致性。

表7.8　锰铜压阻传感器测试试验结果

(www.xing528.com)

图7.37　光纤探针试验测试信号

表7.9　光纤探针传感器测试试验结果

各次试验测试所得冲击波速度D与靶板内粒子速度u的关系如图7.38所示。当飞片撞击速度小于984 m/s时，冲击波速度随粒子速度的增大近似线性增加；但当撞击速度增加到1 240 m/s时，冲击波速度显著减小。基于对冲击波传播规律的认识，对于稳定传播的冲击波，其波速随波幅的增强而增大。结合上文中对不同撞击速度下靶板自由面粒子速度历史曲线的讨论，当撞击速度达到1 240 m/s时，35CrMnSiA钢发生了相变，使冲击波的传播失稳，冲击波波速随波幅增强而变慢，冲击波波阵面发生间断而蜕化为两个波速不同的冲击波。对广泛材料所做的大量试验研究表明，在不发生冲击相变的相当宽的试验压力范围内，冲击波速度D与靶板内粒子速度u呈简单线性关系［299］：

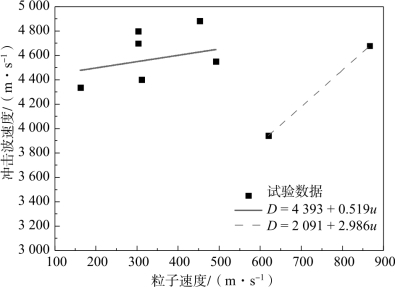
图7.38　冲击波速度与粒子速度关系图

式中，C0和λ为Hugoniot材料常数。如图7.38所示，35CrMnSiA钢在984～1 240 m/s的撞击速度范围内开始出现相变，故利用最小二乘法对D-u关系式进行分段线性拟合，拟合结果列于表7.10中。

表7.10　Hugoniot关系式分段线性拟合结果

在低压低应变率下，材料的弹性段应力-应变是线性关系，但是在高压高应变率下，材料的弹性模量E与剪切模量G都不再是常数，而是随压力变化而变化。在高压下，固体材料抵抗形状变化的能力可以忽略不计，只需要考虑体积变化，因而本构关系就变成了压力与比容的关系［299，304，306，311］。pH-V Hugoniot曲线的解析表达式为：

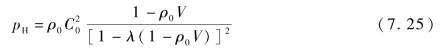
图7.39所示为试验所测的冲击波波阵面上的压力和比容所确定的Hugoniot关系曲线，据此可以确定不同波速的冲击波传过同一初始状态的介质之后所突跃到的终点状态。实测压力值与理论公式计算值一致性较好，证明了上述拟合Hugoniot参数的正确性。此外，由图7.39可见，高压高应变率下35CrMnSiA钢固态相变导致pH-V Hugoniot曲线在17.57～19.19 GPa压力范围内发生间断。

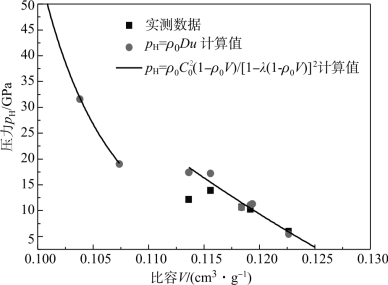
图7.39　35CrMnSiA钢的Hugoniot关系曲线

7.5.2.3　动态响应特性

基于上述对自由面粒子速度历史曲线的结构分析，进一步对一维应变状态下35CrMnSiA钢的动态响应特性进行定量分析。依据平面正冲击波Rankin-Hugoniot突跃变化条件，传播速度较快的塑性波波速可用下式进行计算：

式中，Cp为紧随弹性前驱波E的传播速度较快的塑性波波速；Tt为靶板厚度；te为弹性前驱波E到达靶板自由面的时刻，如图7.40所示；tp为塑性波到达靶板自由面的时刻；Ce为一维应变弹性纵波波速。撞击压力p可用下式进行计算：

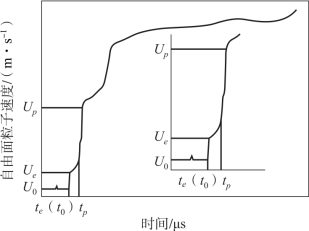
图7.40　冲击波速度与粒子速度关系图

如图7.40所示，自由面粒子速度的阶跃变化是弹性波和塑性波共同作用的结果。由于在高速冲击问题中，弹性波的强度远低于塑性波强度，并且一维应变状态下，弹性纵波波速仅比塑性波波速高25%左右［57］，因此，忽略弹性波的作用，利用塑性波波速来计算应变率：

式中，Up为塑性波作用引起的靶板自由面粒子速度阶跃；U0为靶板自由面粒子速度起跳之前的初始值；t0为靶板自由面粒子速度起跳时刻。Hugoniot弹性极限（HEL）可用下式进行计算：

式中，Ue为弹性波作用引起的靶板自由面粒子速度阶跃。一维应变状态下，材料的等效屈服应力σs可用下式进行计算［57］：

式中，υ是材料的泊松比，对超高强度合金钢，一般取0.3。一维应变状态下，35CrMnSiA钢的动态响应特性计算结果列于表7.11中。

表7.11　一维应变状态下35C rMnSiA钢的动态响应特性

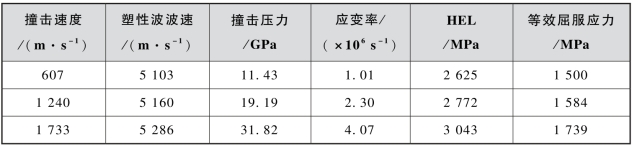
表7.11表明，一维应变状态下35CrMnSiA钢的HEL和等效屈服应力均随应变率的增大而增加。为了对比不同应力状态下35CrMnSiA钢的应变率敏感性，进一步讨论10-3～106 s-1应变率范围内轴向屈服应力和等效屈服应力随应变率的变化规律，并通过计算应变速率敏感指数m［62］对其进行定量表征：

式中，σD和σS分别为动态及准静态加载时材料的屈服应力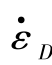；和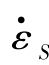为相应的加载应变率，计算结果列于表7.12中。

表7.12　不同应力状态下35CrMnSiA钢的屈服应力和应变率敏感性因子

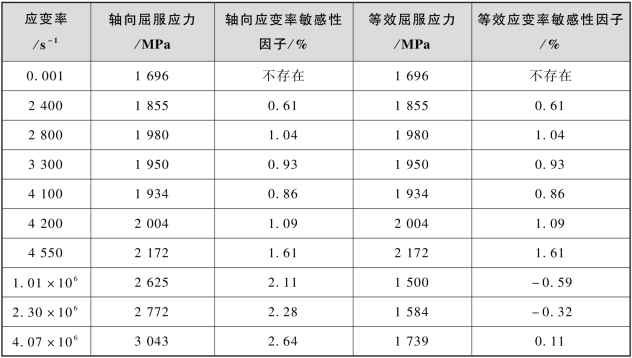
如图7.41（a）和表7.12所示，在10-3～106 s-1应变率范围内，35CrMnSiA钢的轴向屈服应力和轴向应变率敏感性因子随应变率的增加而近似单调递增，在106～106 s-1范围内，材料的应变率敏感系数最大；如图7.41（b）和表7.12所示，在一维应力或一维应变状态下，35CrMnSiA钢的等效屈服应力和等效应变率敏感性因子随应变率的增加而近似单调递增，但1.01×106 s-1和2.30×106 s-1应变率下，材料的等效屈服强度低于准静态等效屈服强度。因此，在数值仿真和理论分析过程中，应注意材料所处的应力状态和应变率范围，谨慎使用等效屈服应力作为材料的失效或侵蚀判据。

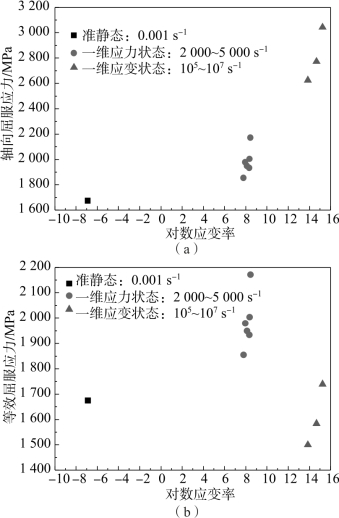
图7.41　不同应力状态下屈服应力随对数应变率的变化关系

为定量分析一维应变状态下高速冲击产生的温升效应，采用Walsh（1957）［312］提出的物态方程计算方法对冲击温升进行简化计算：

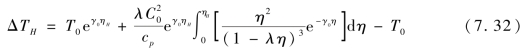
式中，T0为环境温度；C0和λ为Hugoniot参数；γ0由Meyers公式λ＝（γ0＋1）/2［313］计算得到；cp为定压比热；η是体积应变，由式η＝u/D计算得到。该方法适用于可以不考虑电子项贡献及晶格非谐振项贡献的较低压力区，对于固体材料而言，适用于200 GPa以下的冲击压力范围。不同撞击速度和撞击压力下的冲击温升计算结果列于表7.13中。

表7.13　不同撞击速度下35CrMnSiA钢的冲击温升

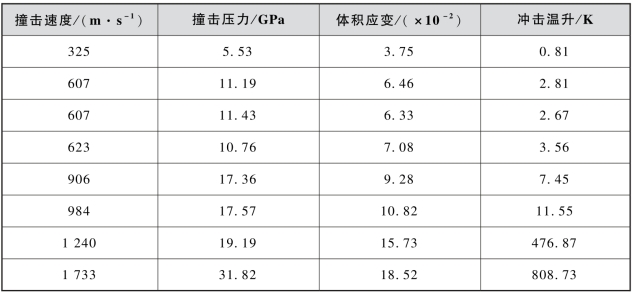
由表7.13可见，当撞击压力小于17.57 GPa时，35CrMnSiA钢靶板的冲击温升均小于12 K，当撞击压力提高到19.19 GPa材料发生相变时，冲击温升从11.55 K突跃变化到476.87 K，可知超高强度合金钢的固态相变伴随着显著的热效应。由于高压高应变率下固体材料抵抗形状变化的能力可以忽略不计，材料不再对剪切强度敏感，因此，35CrMnSiA钢靶板并没有在476.87 K的冲击温升作用下发生绝热剪切破坏。