破片剩余速度与着速的相关性分析

靳佳波［212］（2003）、徐豫新［213］（2010）通过Ls-Dyna软件分别获得了高速杆条和球形钨合金破片在不同着速下的靶后剩余速度，并通过着速与剩余速度的相关曲线，外推获得了破片的弹道极限速度。此方法也被Zukas［58］（1982）应用于试验弹道极限的试验研究。

在此，将表6.9中通过数值模拟获得的弹道极限分别与7.5 m/s（数值模拟获得弹道极限速度时的贯穿速度）、17.5 m/s（7.5＋10）、27.5 m/s（17.5＋10）、47.5 m/s（27.5＋20）、77.5 m/s（47.5＋30）和107.5 m/s（77.5＋30）共6个值求和所获得的数值作为着速，进行同结构破片对不同试验工况靶标侵彻的数值模拟，获得破片的靶后剩余速度。回归曲线如图6.30所示。

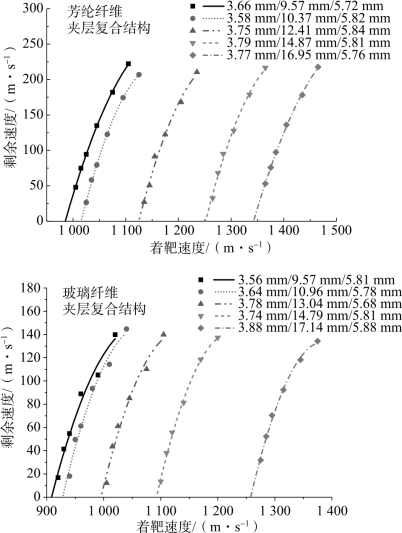
图6.30　破片靶后剩余速度随着速的变化

图6.30中，无论夹层材料为何种纤维，随着破片着速的提高，破片靶后剩余速度也不断递增，递增规律并非线性，近似于二次函数形式。通过外推获得不同试验工况的弹道极限速度列于表6.10中。

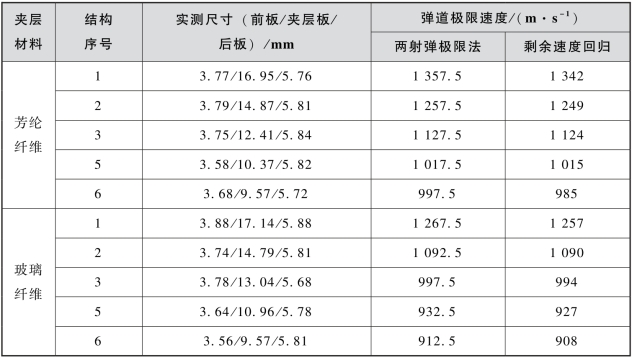
由表6.10可见，外推值均略偏低于同数值模拟模型和参数条件下采用两射弹极限法获得的弹道极限速度值。表明该方法虽然符合弹道极限速度的物理内涵，但由于靶体临近破坏时对局部加载具有敏感性和随机性，通过试验数据统计规律获得的弹道极限速度的可信度更高。

表6.10　不同分析方法获得的弹道极限速度

(www.xing528.com)

将破片对不同结构靶标的着靶速度进行归一化（即获得破片着靶速度与弹道极限之差：7.5 m/s、17.5 m/s、27.5 m/s、47.5 m/s、77.5 m/s和107.5 m/s），根据表6.10获得的着速与弹道极限速度值之差与剩余速度的关系如图6.31所示。

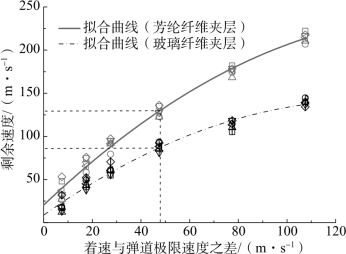
图6.31　着速与弹道极限速度之差随剩余速度的变化

由图6.31可见：

①破片剩余速度随着着速与弹道极限之差的增加而呈二次函数递增；

②同等条件下，芳纶夹层复合结构的靶后速度要高于玻璃纤维夹层复合结构的靶后速度。

③当着速高出弹道极限速度的值大于40 m/s时，靶后剩余速度随着靶标结构变化跳动范围缩小，靶体破坏对局部加载的敏感性对剩余速度的影响开始减弱，此时，无论何种结构，破片的剩余速度均大于50 m/s。