无间隔复合结构的设计与应用优化

4.6.1.1　破片侵彻机理分析

根据第4.5节的试验研究可知，对于无间隔复合结构，韧性钢破片侵彻过程中先开始侵磨合金钢，直至磨透穿出后，对纤维增强复合材料板进行侵彻并贯穿，整个过程为一整体，韧性钢破片并未发生破碎，但是有明显的侵蚀。因此，破片对复合结构的弹道极限计算模型应当作整体考虑。在第4.5节试验中，回收试验后，破片典型形貌列于表4.18中。

表4.18　回收破片的形貌

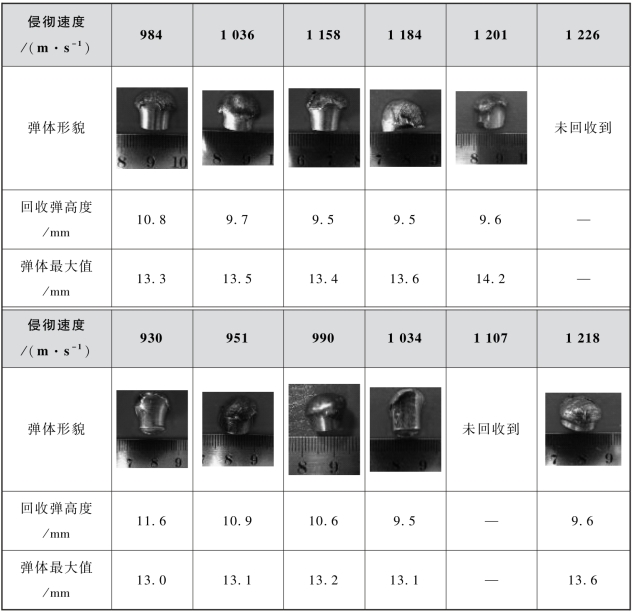
由表4.18可见，弹速侵彻下，未热处理的韧性钢破片发生严重塑性变形，头部被墩粗。试验后，合金钢靶板、纤维板典型破坏形态如图4.11和图4.12所示。

图4.11　前置合金钢靶板典型破坏形貌

（a）迎弹面；（b）背弹面

图4.12　后置芳纶纤维典型破坏形态

（a）迎弹面；（b）背弹面；（c）侧面

图4.11中，前置合金钢靶板迎弹面处翻边成孔，背弹面局部屈曲成孔，同时，形成薄片球冠状塞块，与文献［248］中无约束钢板的破坏模式不同；纤维板迎弹面纤维丝剪切断裂成孔，背弹面拉伸断裂成孔，同时伴有层裂，与文献［244］中无约束破坏模式相同。综合分析，将破片对钢/纤维复合结构的侵彻分为3个阶段：①弹体变形侵入阶段，即破片墩粗变形侵入钢板并挤压侵彻至钢板背弹面开始屈曲盘凸；②钢板背弹面局部屈曲剪切成孔，形成冲塞阶段，即钢板背弹面屈曲盘凸至塞块形成；③破片与塞块共同侵彻纤维板阶段，即破片顶着塞块侵入纤维板至弹体和塞块贯穿纤维板［86］。破片侵彻过程如图4.13所示。

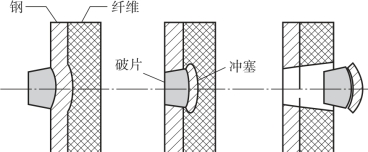
图4.13　破片侵彻过程示意图

据此，可推断破片的动能E0在侵彻过程中转换为前置钢板的屈曲盘凸、破裂成孔、纤维丝的断裂和纤维层间的开裂及弹体墩粗变形。即

式中，E1为前置钢板所吸收的能量，包括形成弹孔所消耗的能量、弹靶接触中形成共同速度所消耗的能量E11及纤维板抵抗前置钢板盘凸变形挤压所消耗的能量E12；E2为后置纤维板拉伸断裂和层裂所吸收的能量；ED为破片与冲塞墩粗的变形能。因此，将式（4.3）代入式（4.2）可得：

4.6.1.2　破片侵彻过程能量转换分析

在此，将破片对钢/纤维复合结构的侵彻过程看作3个相互独立的能量转换过程进行分析，即侵彻前置合金钢板至钢板背部开始盘凸变形、前置合金钢板盘凸变形挤压纤维板至塞块形成、破片与塞块共同侵彻纤维板至贯穿复合板或运动结束3个独立阶段，并做如下假设：

①破片对钢/纤维复合结构侵彻的整个过程遵循能量守恒和动量守恒；

②在900～1 200 m/s的试验速度段，前置合金钢板形成弹孔所消耗的能量为一恒定值，不随撞击速度的变化而改变；

③纤维板在破片侵彻方向近似为同性均匀体，抗破片侵彻性能只与纤维材料的强度和侵彻体的撞击速度相关；破片在侵彻纤维板过程中为一刚体，不发生变形。

据此，建立3个不同阶段的复合结构能量吸收分析模型如下：

（1）破片侵彻前置合金钢板至钢板背部开始盘凸变形阶段

破片侵彻合金钢板所消耗的能量包括弹靶接触中形成共同速度所消耗的能量Es及弹孔形成所消耗的能量Ef。即

根据动量守恒：

根据动能与动量守恒，则破片和冲塞形成共同速度vf所消耗的能量为：(www.xing528.com)

弹孔形成所消耗的能量为：

式中，v0为破片侵彻复合结构的弹道极限速度；vs50为破片侵彻前置合金钢靶板的弹道极限速度。

（2）前置合金钢板盘凸变形挤压纤维板至塞块形成阶段

假设纤维板对前置合金钢板背部鼓包阻力符合H.M.Wen［249］（2000）的理论模型。即抗侵彻阻力分为两部分：一部分是纤维材料自身强度引起的静阻力fe，另一部分是惯性效应引起的动阻力fD。纤维板抗前置合金钢板背部鼓包的阻力F1可写为：

式中，A0为前置合金钢板背面盘凸与纤维板接触的平均横截面积，为0.5×

（1＋λ2）πRP

2，λ为冲塞直径与原弹体直径之比，根据试验结果，λ可取1.25，RP为原弹体半径；σe为纤维板的抗压强度；β为弹体头部形状系数；ρf为纤维板的密度；vd为前置合金钢板背部盘凸变形的平均速度，为最终冲塞塞块速度的一半。

盘凸变形的最终高度H2可视为前置合金钢板盘凸变形挤压纤维板至塞块形成阶段的作用距离，可根据前置钢板的延伸率计算获得。据此，前置合金钢板盘凸变形挤压纤维板至塞块形成过程中所消耗的能量E12可表示为：

（3）破片与冲塞共同侵彻纤维板阶段

同样根据H.M.Wen模型，纤维板抗破片与冲塞的阻力为：

式中，A1为冲塞块与纤维板接触的横截面积，为π（λRP）2，mm2；vf为破片与冲塞的共同速度，为2vd，m/s。在此阶段，破片的作用距离H3为Ha与H2之差，Ha为纤维板的厚度，mm。

据此，破片与冲塞共同侵彻纤维板过程中所消耗的能量E2可表示为：

冲塞与破片墩粗变形能可写成：

式中，σp、σt分别为破片、合金钢材料的屈服强度；Wp、Wt分别为试验后破片和塞块的变形量。

此外，对于芳纶纤维板，尤其是较厚的芳纶纤维板，存在分层吸能，吸能量与芳纶纤维的基体种类及含量相关，即表现为基体与纤维布的耦合力，则该吸能量与芳纶纤维板的厚度相关，见式（4.14）：

式中，K为单位厚度分层吸能量，根据第4章材料选型结果时的试验，可得K为5.6×1010 g·mm/s2；Hfk为芳纶纤维板的厚度，mm。

根据式（4.4），比吸收能可表示为：

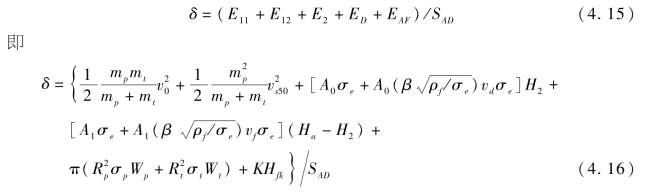
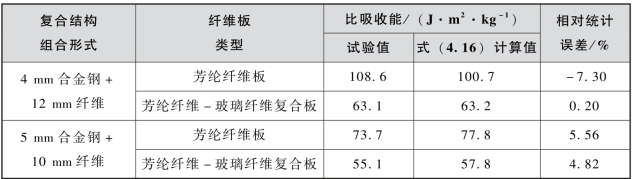
根据获取的纤维板材料参数，采用式（3.13）计算获得7.5 g破片对厚度为4 mm和5 mm合金钢靶板的弹道极限速度，并按半球形计算塞块的质量，根据文献［250］，弹体头部形状系数β取1.5；根据第3章测试获得合金钢板的延伸率，计算4 mm和5 mm前置合金钢板在破片高速侵彻下盘凸变形的最终高度。将上述参量代入式（4.16）中，计算获得不同试验工况下比吸收能的分析值，列于表4.19中。因表4.19中数据较少，并不适合采用基于标准化残差值在标准正态分布区间落入度的方法检验模型，在此采用传统的相对统计误差的方法进行检验。由表4.19可见，分析模型与试验结果相比，相对统计误差不大于8%，表明该分析模型计算结果具有一定的准确性。

表4.19　分析模型与试验结果对比