破片贯穿合金钢靶板后剩余速度数值仿真优化

破片贯穿合金钢靶板后的剩余速度是破片侵彻复合结构研究中的重点关注内容，因破片贯穿靶体后，破片与塞块同时存在，且弹道随机，剩余速度的测试往往难以精准；此外，已有试验表明，在临界速度附近，弹体剩余速度随撞击速度的增加呈非线性增长规律，且塞块的质量难以有效计算，因此，基于能量守恒获得的线性增长函数也无法精确计算破片贯穿合金钢靶板后的剩余速度。

为了分析剩余速度与撞击速度的关系，采用3.3节建立的数值仿真模型，通过数值仿真计算出不同入射速度下破片贯穿合金钢靶板后的剩余速度。将通过数值仿真计算获得的弹道极限分别与50 m/s、100 m/s、200 m/s、300 m/s、400 m/s和500 m/s等相加（直至1 400 m/s以上）作为撞击速度，进行破片以不同撞击速度对4 mm、5 mm、6 mm、7 mm和8 mm厚合金钢靶板侵彻的数值仿真，获得破片的靶后剩余速度，列于表3.35中。根据表3.35，获得破片撞击速度与剩余速度的关系，如图3.27所示。

表3.35　不同撞击速度下破片的靶后余速

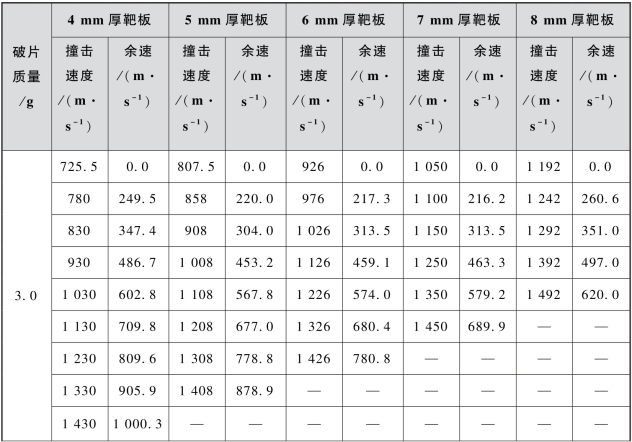
续表

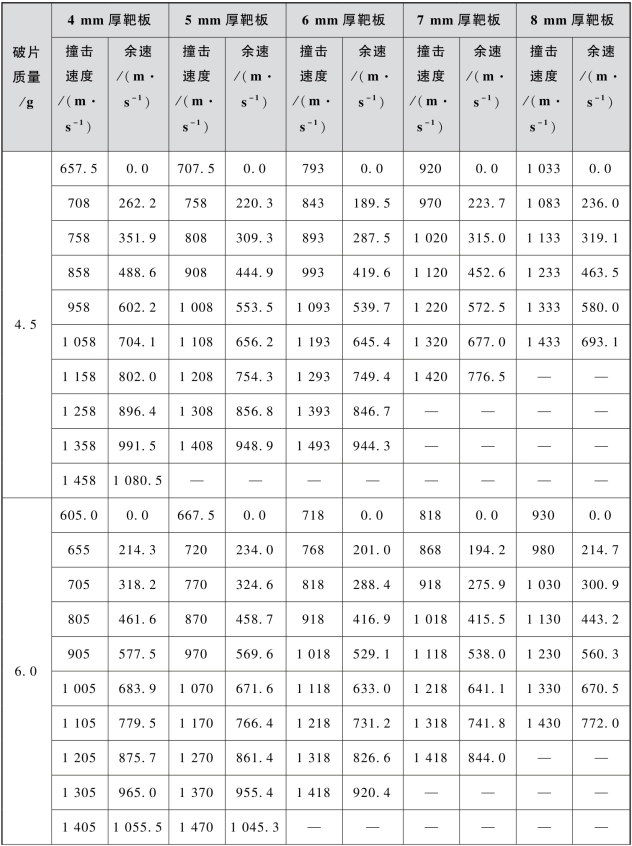
续表

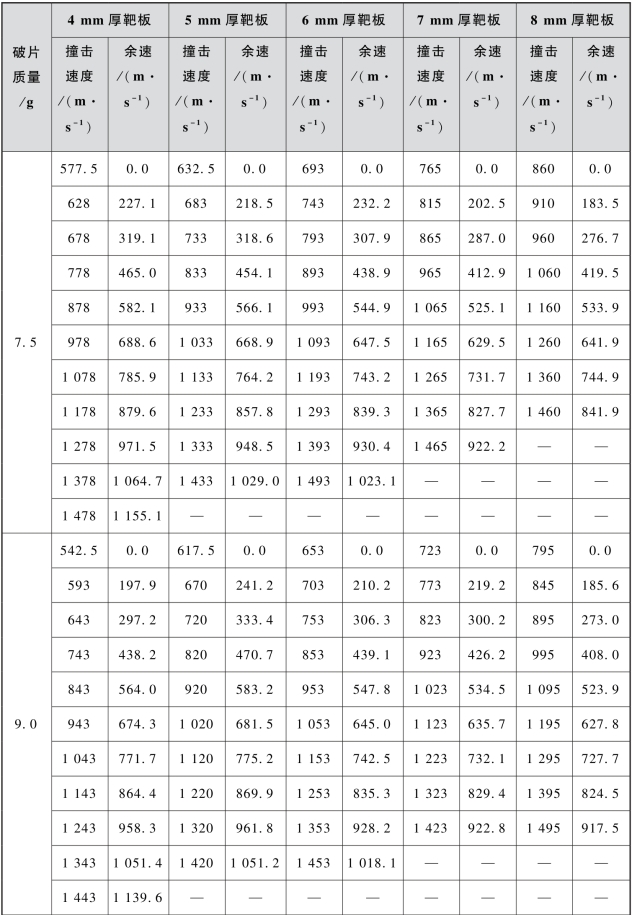
续表

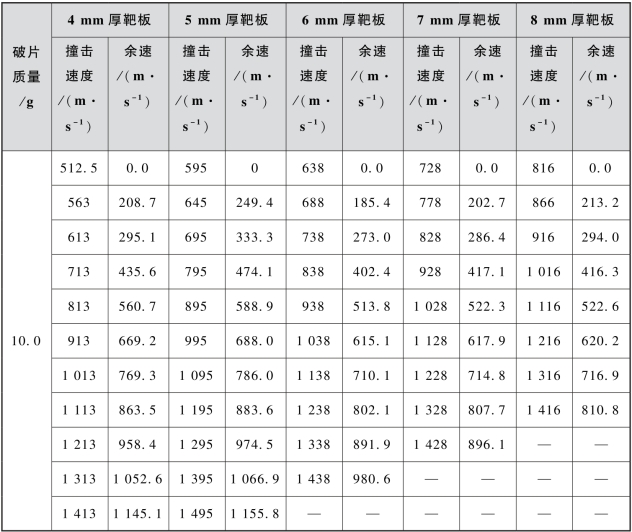(www.xing528.com)

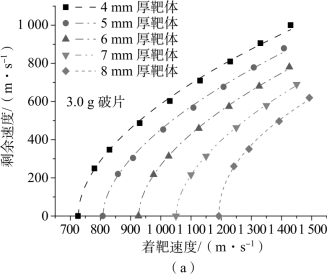
图3.27　撞击速度与剩余速度关系

（a）3.0 g破片

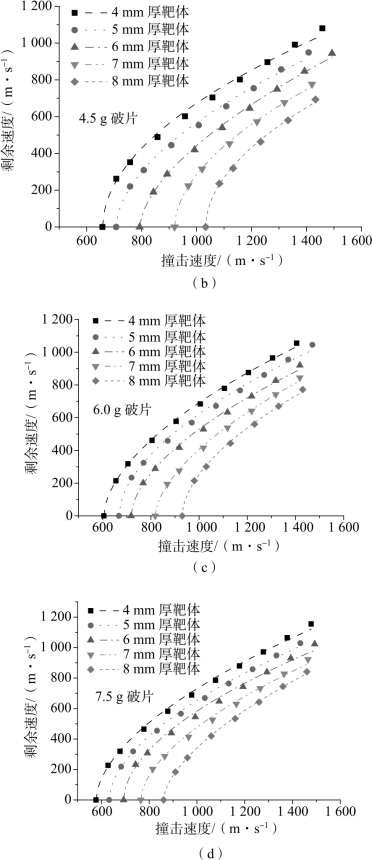
图3.27　撞击速度与剩余速度关系（续）

（b）4.5 g破片；（c）6.0 g破片；（d）7.5 g破片

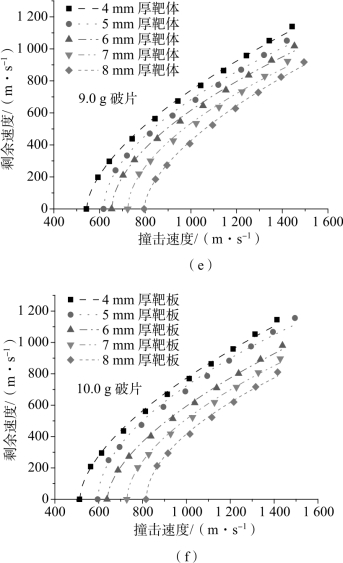
图3.27　撞击速度与剩余速度关系（续）

（e）9.0 g破片；（f）10.0 g破片

由图3.27可见，在破片侵彻合金钢靶板的极限速度以上200 m/s范围内，破片贯穿合金钢靶板后的剩余速度随撞击速度的提高不呈线性变化，与更大撞击速度段的表现不一致。Zukas［58］（1982）通过撞击速度与剩余速度的相关试验曲线回归外推，获得了破片的弹道极限速度；靳佳波［212］（2003）、徐豫新［213］（2010）通过Ls-Dyna软件分别获得了高速杆条和球形钨合金破片在不同撞击速度下的靶后剩余速度后，采用线性函数外推的方法获得了弹道极限速度，均是存在误差的。由图3.27可见，采用撞击速度与剩余速度相关曲线线性外推获得弹体的弹道极限速度应低于实际值。