3.10.3.1 适用范围的增加
在此仍假定仿真值为实际观察值,式(3.14)计算值为估计值,根据仿真计算结果和式(3.14)计算值,可获得6种质量破片对5种厚度合金钢靶板侵彻的弹道极限的残差及标准化残差值,列于表3.30中。
表3.30 式(3.14)计算弹道极限的残差及标准化残差值(靶体厚度:4~8 mm)

由表3.30可见,式(3.14)计算值的标准化残差值全部落在(-2,2)区间以内,表明式(3.14)在更大的弹靶相对厚度范围内具有可靠性。因此,式(3.14)弹靶相对厚度适用范围可适当扩大到1.31~4.20,在此对式(3.14)的适用范围进行修正,获得式(3.16):
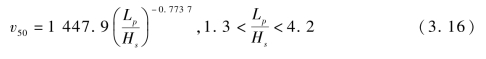
3.10.3.2 无偏修正
由表3.30可获得残差均值为24.72 m/s,残差的样本标准差为40.94 m/s,残差值80%(24/30)为正,如图3.23所示,可知式(3.14)计算结果为有偏估计。
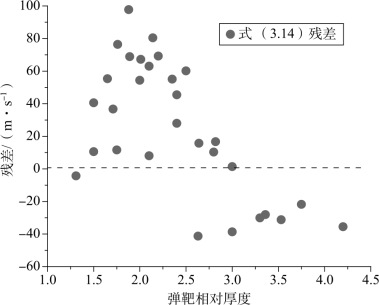
图3.23 式(3.14)计算残差值的分布
因此,对式(3.16)计算模型进行进一步的无偏修正,得到式(3.17):

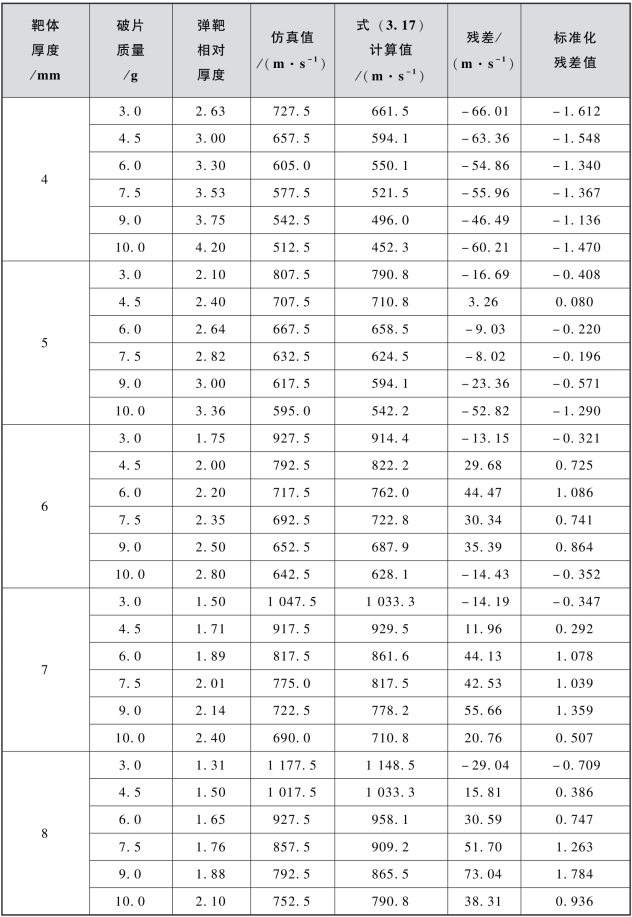
仍假定仿真值为实际观察值,式(3.17)计算值为估计值,根据仿真结果和式(3.17)的计算值可以获得6种质量破片对5种厚度合金钢靶板弹道极限的残差及标准化残差值,列于表3.31中。
由表3.31可见,式(3.17)计算值的标准化残差值全部落在(-2,2)区间以内,残差均值为0 m/s,残差值50%(15/30)为正,为无偏估计。
表3.31 式(3.17)计算弹道极限的残差及标准化残差值(靶体厚度:4~8 mm)
由表3.31可获得式(3.17)计算残差值的分布,如图3.24所示。由图3.24可见,残差值虽在0值上下均匀分布,但集中分布于两个区间,在弹靶相对厚度3.0以上的,残差值全部小于-40 m/s;在弹靶相对厚度2.5以下的,残差值全部大于-40 m/s,在2.5~3.0的为过渡区间。
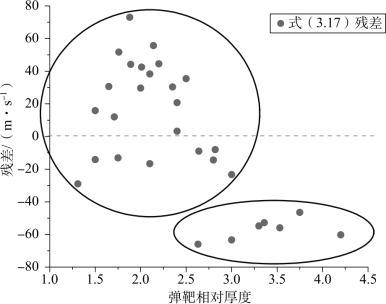
图3.24 式(3.17)计算残差值的分布
3.10.3.3 计算精确度提高
进一步将式(3.17)计算值、仿真值及第3.6节的试验值进行比较,如图3.25所示。
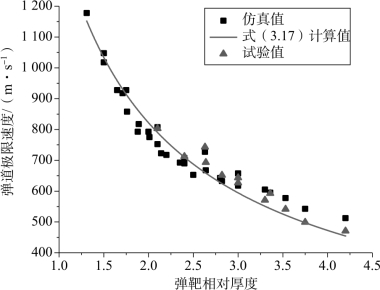
图3.25 式(3.17)计算值、仿真值及试验值对比(https://www.xing528.com)
由图3.25可见,仿真值在弹靶相对厚度为2.5以后出现上偏,在弹靶相对厚度小于2.0和大于2.5的两段趋势并不完全一致,因此采用分段拟合的方式获得式(3.18):

仍假定仿真值为实际观察值,式(3.18)计算值为估计值,根据仿真计算结果和式(3.18)计算值可以获得6种质量破片侵彻5种厚度合金钢靶板弹道极限的残差及标准化残差值,列于表3.32中。
表3.32 式(3.18)计算弹道极限的残差及标准化残差值(靶体厚度:4~8 mm)
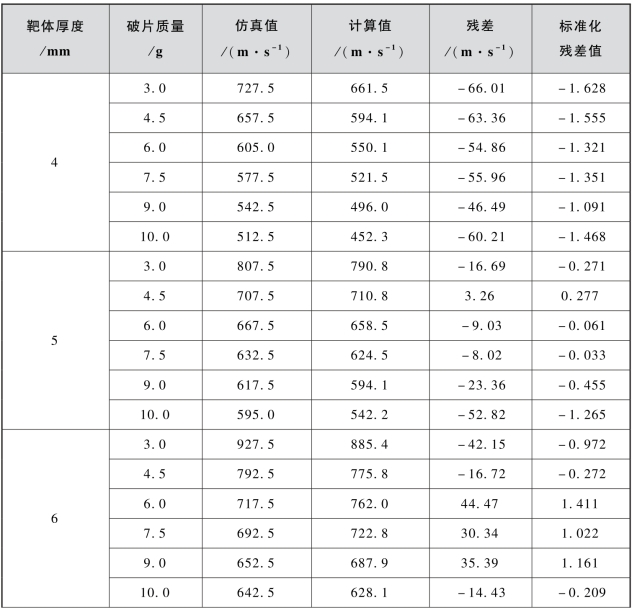
续表
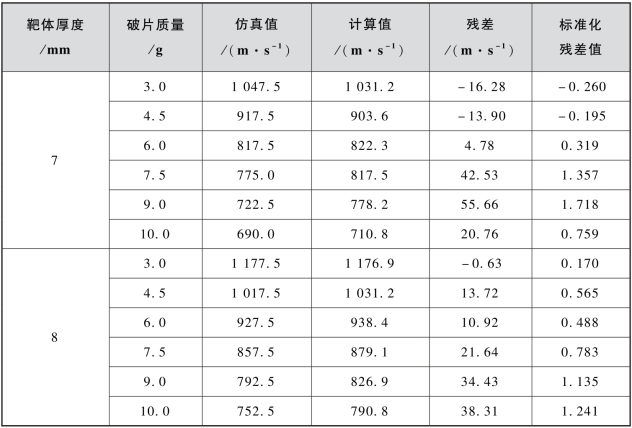
由表3.32可见,式(3.18)计算值的标准化残差值全部落在(-2,2)区间之内。此外,计算可得残差均值为-6.82 m/s,因此,对式(3.18)进一步修正获得式(3.19):

由式(3.17)、式(3.19)计算获得相对仿真值统计误差的极差、残差的均值与标准差列于表3.33中。由表3.33可见,在相同残差均值的条件下,式(3.19)较式(3.17)残差的标准差和相对统计误差的极差更小,表明式(3.19)具有更高的计算精度。
表3.33 式(3.19)与式(3.17)计算结果对比

3.10.3.4 基于破片质量的工程计算模型
在大多数情况下,需要根据破片的质量、靶体的厚度来计算弹道极限速度,以便于工程应用。在此,根据式(3.19)的计算结果,可以获得破片高速侵彻4 mm、5 mm、6 mm、7 mm和8 mm厚合金钢靶板时,破片质量随撞击速度的变化规律,如图3.26所示。由图3.26可见,弹道极限随破片质量的增加呈指数递减。

图3.26 弹道极限随破片质量的变化规律
根据图3.26拟合可以获得破片高速侵彻合金钢靶板的弹道极限随破片质量变化的计算函数式(3.20):

式中,m为破片质量,g;Hs为靶体厚度,mm。
将式(3.20)的计算值和仿真计算结果进行对比,获得弹道极限残差及标准化残差值,列于表3.34中。
由表3.34可见,式(3.20)计算值的标准化残差值全部落在(-2,2)区间以内,表明式(3.20)具有可靠性。此外,通过表3.34计算获得残差均值为0.11 m/s,残差的标准差为34.19 m/s,表明式(3.20)和式(3.19)具有相同的精度和准确度。
表3.34 式(3.20)计算弹道极限的残差及标准化残差值(靶体厚度:4~8 mm)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




