基于弹道极限置信区间的检验方法

在此，结合数理统计的思想，探讨：①特定置信水平下，模型计算结果在弹道极限置信区间落入度；②特定置信水平下，标准化残差值在标准正态分布的置信区间落入度，以及两种分析计算模型可靠性的检验方法。

3.7.3.1　基于弹道极限置信区间的检验方法

置信区间（Confidence Interval）是指由样本统计量所构造的总体参数的估计区间。在统计学中，一个样本的置信区间是对这个样本的某个总体参数的区间估计。置信区间表示这个参数的真实值有一定概率落在真值附近的一个区间，给出的是此区间包含被测参数真实值的可信程度，此概率被称为置信水平。置信水平不同，置信区间的长度将会随之变化。在此，先根据试验结果计算获取不同置信水平的弹道极限置信区间，然后分析由计算模型得到的计算值在特定置信水平的置信区间落入度，并根据落入度来判定分析计算模型的可靠性。

1.弹道极限的置信区间

根据试验结果，按照90%、95%、99%和99.9%置信水平，分别求出3.0 g、4.5 g、6.0 g、7.5 g、9.0 g和10.0 g破片对4 mm和5 mm两种厚度合金钢靶板弹道极限的置信区间与置信区间长度，具体如下：

（1）90%置信水平

按照90%的置信水平，计算结果列于表3.11中。由表3.11可见，置信区间长度最大为33.2 m/s，最小为22.5 m/s，均值为28.2 m/s。

表3.11　弹道极限的置信区间（90%置信水平）

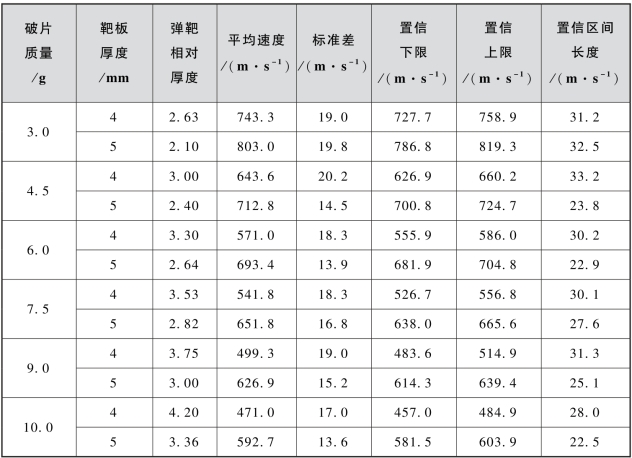
（2）95%置信水平

按照95%的置信水平，计算结果列于表3.12中。由表3.12可见，置信区间长度最大为42.4 m/s，最小为28.6 m/s，均值为36.0 m/s。

（3）99%置信水平

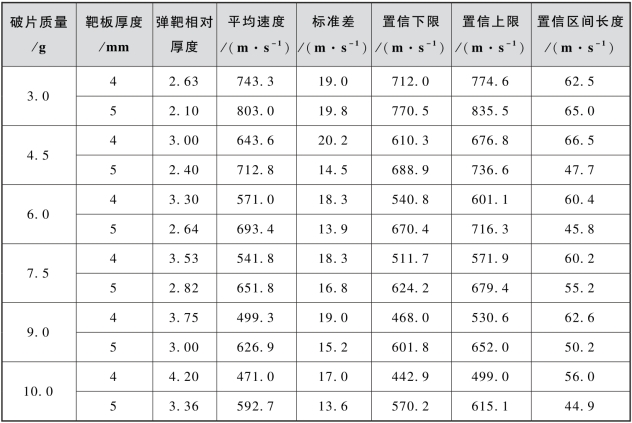
按照99%的置信水平，计算结果列于表3.13中。由表3.13可见，置信区间长度最大为66.5 m/s，最小为44.9 m/s，均值为56.4 m/s。

表3.12　弹道极限的置信区间（95%置信水平）

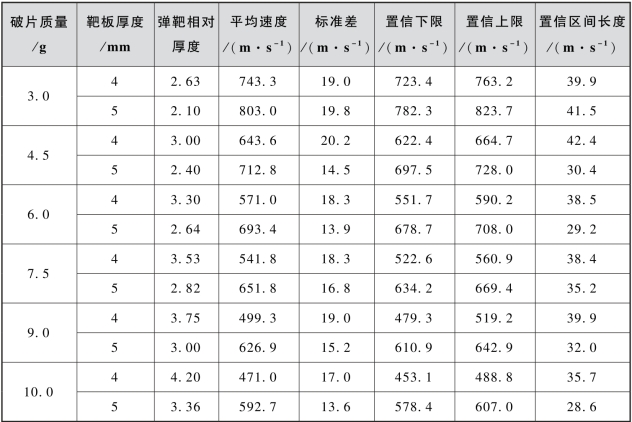
表3.13　弹道极限的置信区间（99%置信水平）

（4）99.9%置信水平

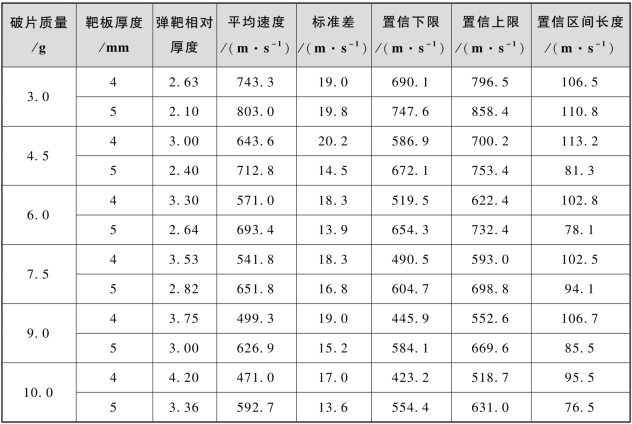
按照99.9%的置信水平，计算结果列于表3.14中。由表3.14可见，置信区间长度最大为113.2 m/s，最小为76.5 m/s，均值为96.1 m/s。

表3.14　弹道极限速度的置信区间（99.9%置信水平）

2.分析讨论

根据表3.11～表3.14获得不同置信水平下置信区间长度与弹道极限关系，如图3.14所示；获得不同置信水平下置信区间长度与标准差的关系，如图3.15所示。由图3.14和图3.15可见，置信区间长度与弹道极限无关，随着试验数据的标准差的增大而不断增加。在统计学中，标准差是反映一个数据集的离散程度的量化形式，也就是说，试验样本值离散度越大，所获得的置信区间的长度就越大。对于本书试验采用六射弹试验法而言，有效试验数据要求最大值和最小值之差不超过45 m/s，所以每个弹道极限的标准差不会超过22.5 m/s，但由于材料的均质、非均质、各向异性，以及缺陷的存在，每种材料的100%贯穿速度和0%贯穿速度之间存在一个被贯穿和未被贯穿交叉混杂出现的混合结果速度区域并不相同。若试验量足够大，即以不同的速度梯度值进行多次射击，通过十几甚至几十发试验数据的标准差分析就可获得这个混合区域大小。本书试验量虽不大，但根据试验结果仍可以看出获取弹道极限数据的标准差最大为20.2 m/s；那么对于试验研究用典型高强度低合金钢的混合区，在试验速度段不会超过40.4 m/s，但这个混合区大小是否与撞击速度有关，从已有的试验数据中尚难以推断。

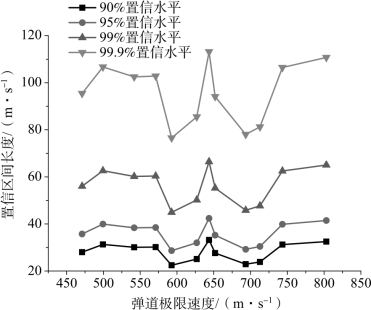
图3.14　置信区间长度与弹道极限速度的关系

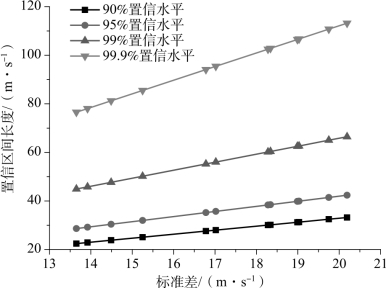
图3.15　置信区间长度与标准差的关系

3.分析计算模型的检验

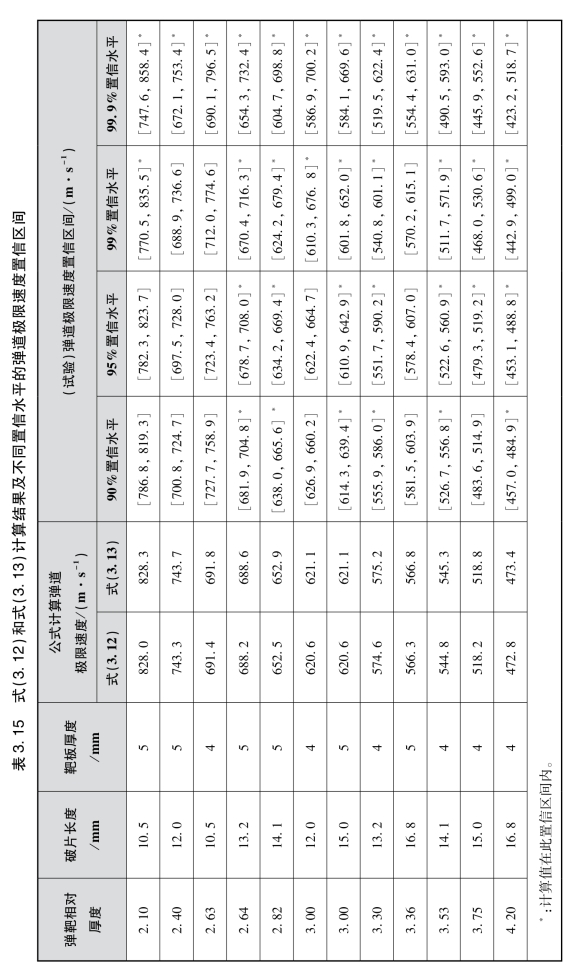
将由式（3.12）和式（3.13）计算获得的试验点的弹道极限速度及表3.11～表3.14给出的置信区间列于表3.15中。由表3.15可见，对于式（3.12）和式（3.13）计算得到的弹道极限速度结果在90%置信水平的置信区间落入度为50%（6/12），在95%置信水平的置信区间落入度为58.3%（7/12），在99%置信水平的置信区间落入度为75%（9/12），在99.9%置信水平的置信区间落入度为100%（12/12）。由上述分析可见，随着置信水平的提升，弹道极限速度结果的落入度在提高，这与随着置信水平提高，置信区间的长度增加是相关的，并且式（3.12）和式（3.13）计算得到的结果不在置信区间的点主要集中在弹靶相对厚度较小的情况。

观察图3.13的拟合曲线，可以得出弹靶相对厚度为2.63时，弹道极限点较其余点偏离拟合曲线较多，因此，将此点去掉后重新拟合，如图3.16所示，获得计算模型式（3.14）。

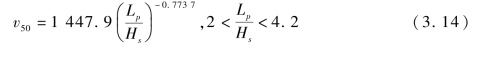
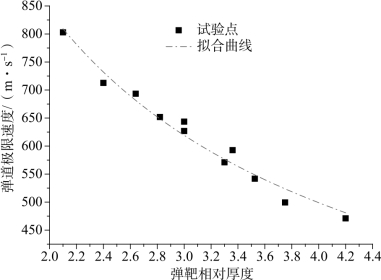
图3.16　弹道极限速度随弹靶相对厚度的变化（11个试验点）(www.xing528.com)

将式（3.14）的计算结果与试验值进行对比，列于表3.16中。

表3.16　式（3.14）计算值与相对统计误差

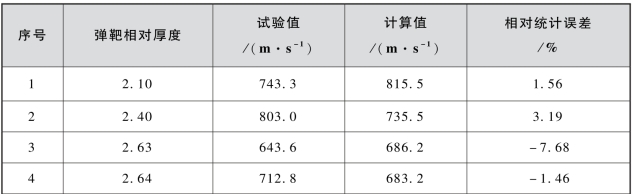
续表

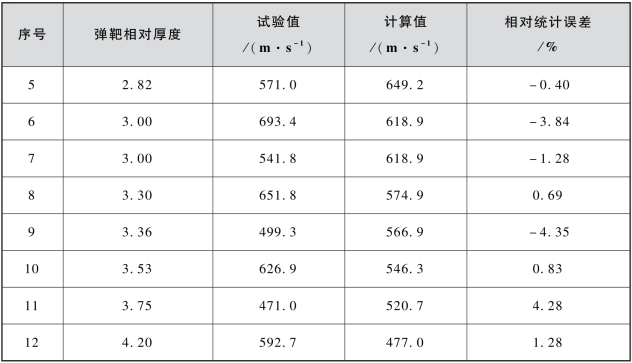
由表3.16可见，式（3.14）计算结果与试验值相对统计误差最大为4.28%，最小为-7.68%，相对统计误差的极差为11.96%，与式（3.13）的极差11.27%相差不大。根据式（3.14）计算获得的弹道极限速度及表3.11～表3.14给出的置信区间列于表3.17中。

由表3.17可见，对于式（3.14）计算得到的弹道极限速度在90%置信水平的置信区间落入度为58.3%（7/12），在95%置信水平的置信区间落入度为58.3%（7/12），在99%置信水平的置信区间落入度为83.3%（10/12），在99.9%置信水平的置信区间落入度为91.7%（11/12）。根据表3.15和表3.17，可得式（3.13）和式（3.14）的计算结果在置信区间落入度随置信水平的变化规律，如图3.17所示。

由表3.15、表3.17和图3.17可见，由于将弹靶相对厚度为2.63的点去除，在低置信水平时，式（3.14）较式（3.13）具有较高的落入度，即可靠性更高；但当置信水平达到99.9%时，因式（3.14）并未考虑弹靶相对厚度为2.63时的点，所以式（3.14）的落入度要低于式（3.13）；而置信水平达到99.9%时，置信区间非常宽，置信区间长度均值为96.1 m/s，为试验限定速度差45 m/s的2.136倍，说明较大的置信区间将扩大容差范围。

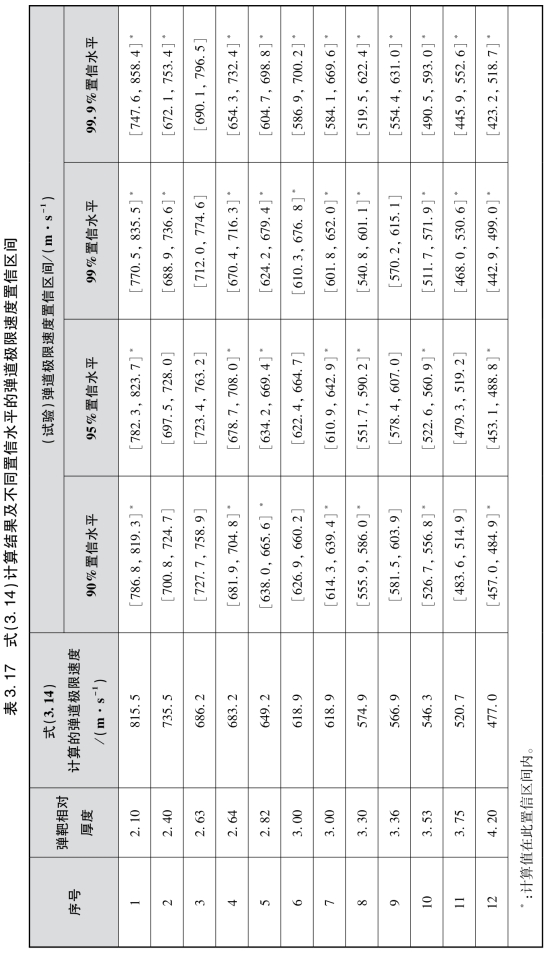
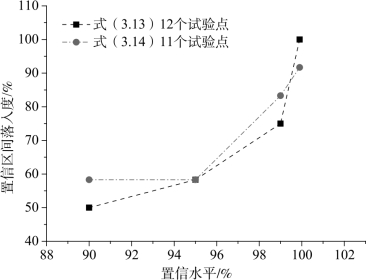
图3.17　计算结果在置信区间落入度随置信水平的变化

3.7.3.2　基于标准化残差值的检验方法

1.残差及残差的标准化

在数理统计中，残差是指实际观察值与估计值（拟合值）之间的差值。在回归分析中，测定值与按回归方程预测的值之差，即为残差，残差遵从正态分布。显然，有多少对数据，就有多少个残差，便可根据多个残差获取残差的数字特征。定义标准化残差为残差和残差均值之差与残差的标准差的比值，即式（3.15）：

式中，为第i个标准化残差值；δi为第i个残差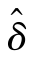；为N个残差的平均值；δs为N个残差的标准差。

“残差”蕴含了有关模型基本假设的重要信息，对于通过回归分析获得的数学模型，实质是用连续曲线近似地刻画或比拟平面上的离散点组，以表示坐标之间函数关系的一种数据处理方法。残差分析就是利用残差表征数据点与它在回归直线上相应位置的差异信息，来考察模型假设的合理性及数据的可靠性。在此，本书采用基于残差分析的方法对计算模型进行检验［205，206］。

2.分析计算模型的检验

首先，根据试验数据，将式（3.12）和式（3.13）的计算结果与试验值相比较，获得残差和标准化残差值，列于表3.18和表3.19中。

表3.18　式（3.12）计算结果的残差和标准化残差值

表3.19　式（3.13）计算结果的残差和标准化残差值

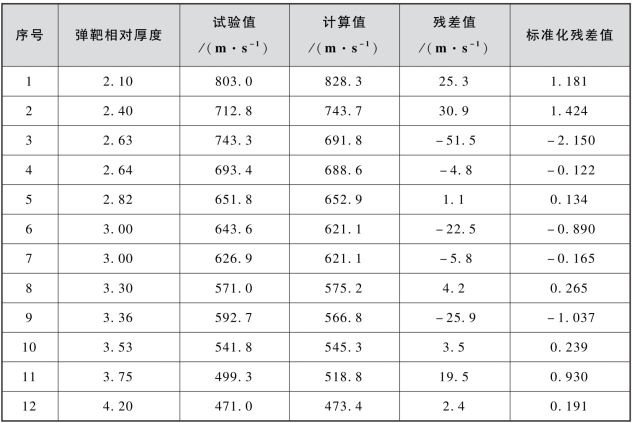
因残差服从正态分布，因此标准化残差值服从标准正态分布，可知标准化残差值落在（-2，2）区间以外的概率p≤0.05。根据统计学原理，若某一变量的标准化残差值落在（-2，2）区间以外，则可在95%置信水平将其判为异常试验点，不参与回归直线拟合。由表3.18和表3.19可知，当弹靶相对厚度为2.63时，标准化残差值分别为-2.145和-2.150，均落在（-2，2）区间以外，如图3.18所示。此外，由图3.18可见，式（3.12）和式（3.13）的标准化残差值极度吻合，再一次表明，基于多组数据直接拟合和基于多组数据求平均值后，拟合的结果具有一致性。

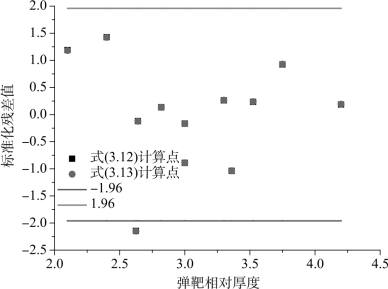
图3.18　式（3.12）和式（3.13）标准化残差值对比

因此，可将弹靶相对厚度为2.63的点判为异常试验点，重新拟合即获得式（3.14），根据式（3.14）获得相应的弹道极限速度计算值，并获得残差及标准化残差值列于表3.20中。

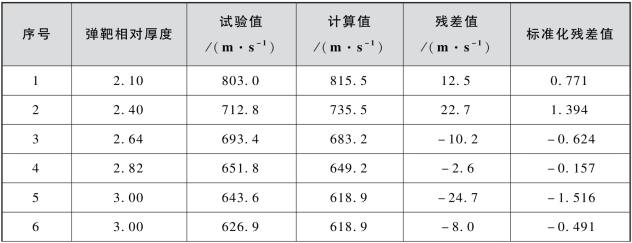
表3.20　式（3.14）计算结果的残差和标准化残差值

续表

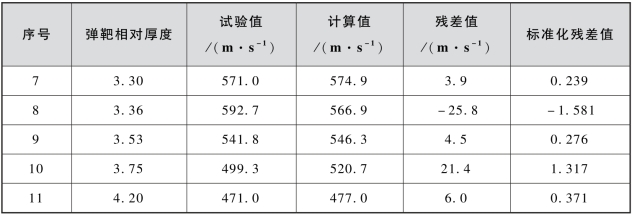
由表3.20可见，所有点均落在了（-2，2）区间以内；由3.7.3.1小节可知，对于90%、95%和99%的置信水平，式（3.14）计算结果在置信区间落入度均不低于式（3.13），则式（3.14）应较式（3.13）具有可靠性。但弹靶相对厚度为2.63时的试验异常点是试验本身的原因还是由于计算模型函数不够合理，覆盖面有限，尚不能从已有的试验数据确定，需要进一步的试验研究；在此，并无后续的试验数据支持，不再做深入讨论。

此外，通过上述分析可见，即使相同弹靶材料的高速侵彻试验，因存在多种随机因素，在单个弹道极限点上具有试验点离散性的同时，在多个弹道极限点上也具有离散性，且弹道极限点越多，离散性可能就越大，涵盖多种情况的分析计算模型就需大量试验获得。例如，本书试验中弹靶相对厚度为2.63的点为异常点，既有本身事实就是如此，所推导的模型函数不能有效反映这一事实的可能；又有试验中靶体、弹体随机因素及测速异常等可能。因此，要获得精确的分析计算模型，需要不断地进行试验，并对所获得的试验数据进行统计分析。