Johnson-Cook模型参数拟合靶体钢试验研究

选择合适的本构模型来描述材料的力学性能，是工程应用普遍采用的一种方法［195］。Johnson-Cook模型［170］是一种经验性的黏塑性本构模型，由G.R.Johnson和W.H.Cook在1983年第7届国际弹道会议上提出。该模型是描述金属变形中与应变硬化、温度、应变率相关的计算模型。由于它的计算结果与试验数据比较吻合，因此在计算中被广泛应用［196，197］。根据3.2.2节和3.2.3节获得的试验数据，对试验研究用合金钢进行J-C本构模型参数拟合如下。

J-C材料模型表达式见式（3.1）：

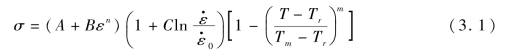
式中，A、B、C、m、n为材料参数，需要通过不同应变率和不同温度条件下的应力-应变试验曲线进行拟合来获取；一般取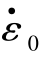＝10-3 s-1；Tm为熔化温度；Tr为室温（290～300 K）；A为应变率10-3 s-1条件下的屈服强度；B、n为应变硬化系数；C为应变率效应系数；m为温度效应系数。

J-C材料模型表达式分为三项，各项之间相互独立，意义明确。第一项表示应变硬化效应，第二项表示应变率效应，第三项表示温度效应。

若不考虑J-C材料模型中的温度软化效应，即温度始终保持在室温［198］，T＝Tr，m＝1，则J-C模型可简化为：

根据试验得到的数据，采用最小二乘法（LSM）对本构方程中的参数A、B、C、n进行拟合，具体参数拟合步骤如下：

（1）确定A

式（3.1）右边第一个括号表示T＝Tr及ε·＝ε·0时的应力-应变关系。在室温条件下，T＝Tr，根据文献［199］，拟合动态本构模型中采用合金钢的静态力学性能试验测量所得的应力-应变曲线可以确定参数A的值。此时，式（3.2）可表示为

当ε＝0时，A即为材料的屈服应力。

（2）确定参数B和n

将式（3.3）移项后，两端取对数，可得

采用最小二乘法对参数B和n进行拟合，可以求得B与n。

（3）确定参数C(www.xing528.com)

参数C是材料应变率敏感系数，当T＝Tr及ε＝0时，式（3.2）可变为

将式（3.5）变形，可得

式（3.6）中，横坐标为ln，纵坐标为，可得C为斜率。利用动态力学性能测试中材料的屈服应力与应变率的关系，采用最小二乘法进行拟合，可得参数C。

按照上述步骤拟合获得试验研究用合金钢的J-C模型参数，列于表3.6中。

表3.6　试验研究用合金钢的J-C模型参数

将拟合获得的参数带入式（3.2）中，可得试验研究用合金钢的本构方程为：

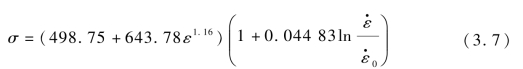
将式（3.7）的计算结果与试验结果进行对比，如图3.5所示（图中直线为公式拟合曲线，曲线为试验结果），可以得出公式拟合结果与试验结果较为吻合，说明J-C模型可以描述试验研究用合金钢的本构关系，该参数可用于后续的破片侵彻合金钢靶板数值仿真计算。

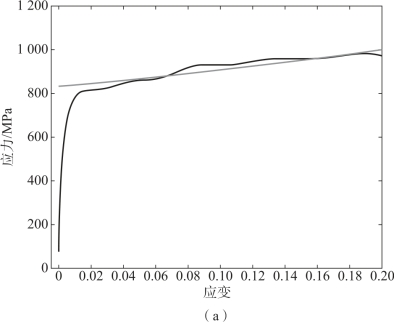
图3.5　J-C模型拟合的应力-应变曲线与试验曲线的比较

（a）应变率为3 241

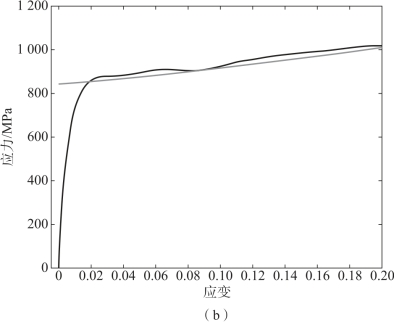
图3.5　J-C模型拟合的应力-应变曲线与试验曲线的比较（续）

（b）应变率为4 707