2.5.2.1 入口孔径计算模型
长期以来,靶孔孔径计算研究大多集中于超高速碰撞条件下厚靶成坑的试验观察和数值仿真分析,获得了若干坑深和孔径的计算公式,如Summers和Charters[142](1958)、P.S.Westine和S.A.Mullin[143](1987)、孙庚辰[144](1994)等各自提出了不同的计算模型,为空间防护结构设计提供了依据。另外,就射流超高速侵彻过程中的径向扩孔,Szendrei[145](1983)基于修正的伯努利方程提出了分析模型,M.Held[146,147](1995,1999)修正了Szendrei的方法,完善了高速流体撞击径向扩孔理论,此后的若干计算方法都是以此为基础获得的。相对超高速碰撞,高速侵彻时,液化效应存在,但不显著,材料高应变率下动态屈服中伴随塑性流动,整个过程动态响应现象复杂、历时短,靶孔几何特征量长期以试验归纳获取为主,如R.F.Recht[148](1977—1978)在试验观察的基础上认为,靶孔孔径为初始弹径的1.25倍;午新民[25](1999)通过研究认为,若着靶速度大于1.0 km/s,靶孔孔径是原弹径的1.34倍;陈志斌[63](2007)以大量试验分析为基础,拟合获得了含着靶速度,弹、靶密度等相关参量的计算模型。在此,简化弹靶初始作用过程,将破片刚性侵入与靶体塑性变形看作两个相互独立的过程进行分析,则复杂的破片侵入过程可分为三个独立阶段:
①初始加载阶段:破片撞击瞬间,在弹靶碰撞点形成强动载荷;
②破片挤入阶段:在强动载荷作用下,破片瞬间挤入,其最大横截面共面于靶体表面;
③横向扩孔阶段:破片前向运动受阻,发生塑性变形,驱动靶孔沿弹靶界面不断横向扩孔。
上述三个阶段如图2.30所示。

图2.30 破片挤入横向扩孔的三个阶段
(a)初始加载阶段;(b)破片挤入阶段;(c)横向扩孔阶段
在初始加载阶段。根据弹靶碰撞冲击波理论,求得靶体内质点运动的速度ut,则弹靶界面运动速度为:
![]()
式中,vp为破片的着靶速度。
在破片挤入阶段,因球形破片尺寸较小,且挤入速度较高,假定:弹靶界面的运动速度近似相等,即球面上各个方向的运动速度近似相等。
在横向扩孔阶段,靶孔径向扩张源于弹靶界面的径向驱动,假定:径向扩孔界面速度随着孔径的增大而减小,成线性分布。根据牛顿第二定律,扩孔过程可描述成:
![]()
式中,mtd为靶体变形质量;atd为靶体变形加速度;Ftd为靶体的变形阻力。对靶孔以近球形进行变形运动,式(2.24)可写成:

式中,rtd为侵彻过程中某一时刻的靶孔直径,与破片瞬时横向直径rpd相等,根据假设,靶孔孔径关于时间求导则为弹靶界面的运动速度,即

 为材料的动态屈服强度,与材料的应变率相关,因靶材的变形阻力远远小于因惯性效应产生的惯性阻力,因此,采用常用的Cowper-Symonds[149](1957)本构关系式(2.27),由材料静态屈服强度
为材料的动态屈服强度,与材料的应变率相关,因靶材的变形阻力远远小于因惯性效应产生的惯性阻力,因此,采用常用的Cowper-Symonds[149](1957)本构关系式(2.27),由材料静态屈服强度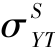 获得材料的动态屈服强度:
获得材料的动态屈服强度:

式中, 为应变率;ε0和r为材料常数,对于低碳钢,分别为40.4和5[150]。定义red为靶孔入口处的终态孔径,则
为应变率;ε0和r为材料常数,对于低碳钢,分别为40.4和5[150]。定义red为靶孔入口处的终态孔径,则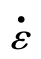 可由下式计算得出。
可由下式计算得出。

式中,taction为破片横向扩孔所用时间;red为破片终态半径,即靶孔入口处孔径;rd为球形破片初始半径。破片塑性变形停止,即靶孔入口孔径达到最大时,破片整体通常已完全进入靶体。因此,破片横向扩孔所用时间可通过下式近似求得:
![]() (https://www.xing528.com)
(https://www.xing528.com)
把式(2.29)代入式(2.28),可得:

把式(2.26)代入式(2.25),消去d t,同时将式(2.30)代入式(2.27)后,代入式(2.25)中,经变换整理,可得:
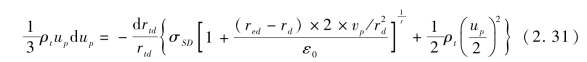
对式(2.31)两边进行积分,整理后可得:
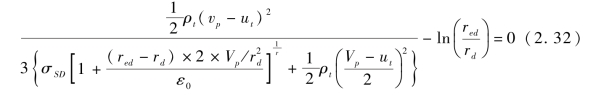
式(2.32)难以直接求解,可采用对分法编写解算程序进行求解。对于93W,采用张江跃[151](1997)提供的Hugoniot参数进行计算,获得的结果与午新民[25](1999)、陈志斌[63](2005)的经验公式计算结果的对比示于图2.31中。
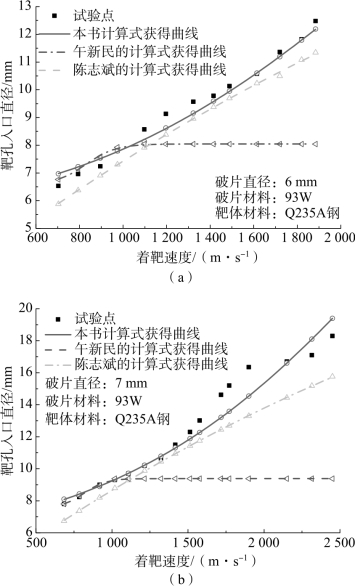
图2.31 靶孔入口处孔径计算与试验结果对比
(a)φ6 mm(93W)钨球;(b)φ7 mm(93W)钨球
由图2.31可见:
①基于上述分析模型解算获得的计算结果与试验吻合良好,误差在10%以内,表明该分析模型可正确描述刚塑性球弹高速侵彻塑性靶体的扩孔过程,分析模型计算结果具有可靠性。
②靶孔入口孔径随着着速的提高而呈非线性函数递增关系。
进行量纲化1分析,获得靶孔入口孔径相对破片原直径增加量φ,即
![]()
式中,Deid为靶孔的入口孔径;Dp为破片直径。φ随着着靶速度提高的关系示于图2.32中。由图2.32可见,靶孔入口孔径相对于破片原直径增加量随着着靶速度的提高呈二次函数增长,即弹体孔径增加量与着靶速度成二次函数关系,与由式(2.8)得出的结论一致。此外,由图2.32可拟合获得靶孔入口的计算关系式(2.34)。

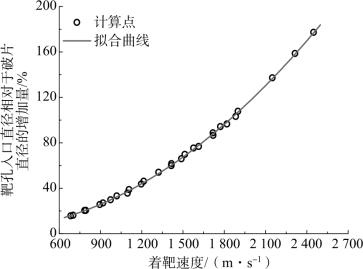
图2.32 靶孔入口处孔径相对于破片原直径增加量随着着速的变化
2.5.2.2 出口孔径计算模型
靶孔出口孔径与破片着靶速度及靶体厚度相关。随靶体厚度不断增加,破片的弹道极限不断提高,破片横向效应增强的同时,周边侵蚀破坏越发剧烈,着靶速度增加到某一值后,靶孔出口孔径不再增加,反而减少。由2.2.3节的试验结果可发现,对于1 500 m/s以下的着靶速度,靶孔基本上是一个等直径圆柱形,当着靶速度大于1 500 m/s后,入口孔径略大于出口孔径。对试验后靶孔出口孔径进行测量,拟合获得临界贯穿条件下,破片出口孔径计算式如下:
![]()
式中,Deod为临界贯穿条件下的靶孔出口孔径;λ为试验系数,可由式(2.36)计算获得。
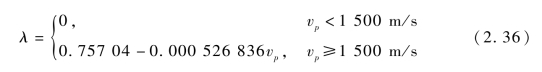
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




