试验结果和分析

2.3.3.1　试验内容

采用2.3.2节中设计的试验系统，针对4种破片：φ6 mm（93W）、φ6 mm（95W）、φ7 mm（93W）、φ7.5 mm（95W），示于图2.12中；两类材料8种靶体：Q235A钢（10 mm厚、12 mm厚、14 mm厚、16 mm厚、18 mm厚、20 mm厚）和2A12-T4铝（10 mm厚、20 mm厚），进行破片穿甲试验。

图2.12　试验所用的4种破片

2.3.3.2　试验结果

弹道枪、轻气炮加载钨合金破片对有限厚金属靶的穿甲试验分别在中国兵器5103厂和北京理工大学西山实验室完成，采用六射弹弹道极限试验法获得4种破片对8种靶体的弹道极限。试验中，任一有效弹道的极限速度的获得均需进行9～14发试验，通过436发试验（弹道枪：401发、轻气炮：25发）获得了4种破片对8种靶板的弹道极限速度，列于表2.5中。

表2.5　弹道极限试验结果

2.3.3.3　现象及数据分析

1.试验现象分析

（1）对有限厚钢靶的穿甲

钨合金破片对有限厚Q235A钢靶的穿甲试验中，93W、95W两种材料破片均出现了明显的塑性变形。随着着靶速度的提高，其破坏形式一致表现为：小变形→半球状变形→铁饼状变形→球壳状变形→薄片，破片的断裂从球弹周边开始，最终发展到芯部，如图2.13所示。

靶板成孔口扩展型破坏，靶孔入口直径随着靶速度的提高而增大，当着靶速度低于2 000 m/s时，靶孔基本上为一圆柱形孔，靶孔内表面大部分为白色光滑侵彻穿孔，靠近出口一小部分为冲塞形成的灰色粗糙圆柱孔，靶孔前靶面产生翻边，背面产生突沿；当着靶速度大于2 000 m/s时，未被穿透的弹坑呈不规则钟形，靶孔内表面大部分为白色粗糙侵彻穿孔，如图2.14所示。当着靶速度提高至1 500 m/s以上时，入口直径略大于出口直径。

图2.13　回收的破片

（a）781.3 m/s；（b）1 019.4 m/s；（c）1 492.7 m/s；（d）1 625.2 m/s

图2.14　不同着速下的靶孔

（a）1 475 m/s；（b）1 900 m/s；（c）2 150 m/s；（d）2 315 m/s

（2）对有限厚铝靶的穿甲

钨合金破片对有限厚2A12-T4铝靶的穿甲试验中，即使着靶速度达到1 500 m/s，93W、95W两种材料破片基本无塑性变形，如图2.15所示，穿甲过程中呈刚性特征，破片贯穿铝靶后，表面挂铝；靶板呈脆性挤凿型破坏，靶孔前靶面无翻边，若破片未贯穿靶板，靶板背面产生凸起的裂纹，裂纹从中心开始；若破片贯穿靶板，靶板背面无突沿；靶孔入口与出口直径一致，略小于球弹直径，推测略有弹性回弹。

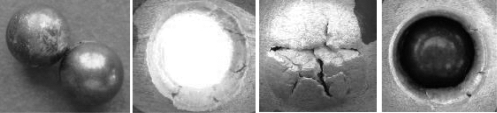
图2.15　回收破片及铝板破坏特征

综上所述，钨合金破片对（钢、铝）两种金属靶体穿甲过程中，弹、靶响应现象不尽相同，对于低密度、低延伸率的铝靶，破片无塑性变形和横向扩孔；对于高密度、高延伸率的钢靶，破片塑性变形和横向扩孔效应随着着靶速度的提高而不断增加。

2.试验数据分析

（1）破片临界贯穿动能、比动能的影响因素

根据表2.5中的试验结果，进行4种破片贯穿同厚度Q235A钢、2A12铝两种金属靶（均为10 mm厚）所需临界动能、比动能的对比，如图2.16和图2.17所示。

图2.16　4种破片的临界贯穿动能

图2.17　4种破片的临界贯穿比动能

分析图2.16和图2.17可知，2A12-T4铝的屈服、拉伸强度虽不低于Q235钢，但破片临界贯穿动能、比动能远远小于Q235A钢板。可见，破片高速撞击条件下，靶体材料强度已非影响破片穿甲能力的主要因素，因靶体密度、着靶速度等性能致使破片的变形、侵蚀及破裂是影响其穿甲能力的主要原因。

另外，由图2.17可见，破片贯穿10 mm钢靶的临界贯穿比动能随着破片直径的增大而减小。进一步分析破片临界贯穿动能与弹靶相对厚度的关系，以及破片临界贯穿比动能与靶体厚度的关系，如图2.18和图2.19所示。

图2.18　临界贯穿动能与弹靶相对厚度的关系

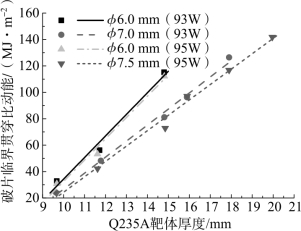
图2.19　临界贯穿比动能与靶体厚度的关系

由图2.18和图2.19可知：

①破片临界贯穿动能、临界贯穿比动能随破片直径与靶厚之比（简称弹靶相对厚度）、靶体厚度增加均呈线性关系递增。对于不同尺寸破片，递增规律有所不同。

②破片、靶体结构尺寸对临界贯穿动能、比动能的影响远大于93W、95W两种材料的差异。

分析单位靶体厚度临界贯穿比动能（Es＝0.5/（AT），A为弹体横截面积，T为靶厚）与弹道极限的关系，如图2.20所示。

由图2.20可知，单位靶体厚度临界贯穿比动能随着弹道极限的增加而呈线性函数关系增长，则可得：

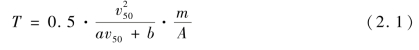(www.xing528.com)

式中，T为靶体厚度，mm；m为破片质量，kg；v50为弹道极限速度，m/s；a、b为拟合系数，分别为4.772×106（J·s）m4、-1 149.2×106 J/m3（R2＝0.996）；A为破片的横截面积，m2。由式（2.1）可知，破片对钢靶的贯穿厚度与其面密度（m/A）及着靶速度相关，对于93W、95W破片，面密度几乎一致，穿甲能力也基本相当，这与表2.5中的试验结果相一致。而对于特定厚度Q235A钢靶的弹道极限，可以通过式（2.1）的变换式（2.2）计算得出。

图2.20　单位靶体厚度临界贯穿比动能与弹道极限速度的关系

（2）靶体临界贯穿的相关性

由冲击相似律分析可见［124］，破片对有限厚度金属靶板的弹道极限速度一般方程可以写成：

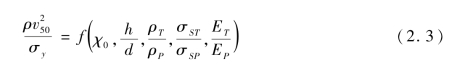
式中，ρP、ρT为破片和靶板材料的密度；σSP，σST为破片和靶板材料强度极限；v50为弹道极限速度；χ0为破片形状系数；h为靶板厚度；d为破片特征尺寸；EP、ET为破片和靶板材料的弹性模量。具体问题中，可以根据弹靶碰撞产生的冲击压力（pS）与弹体材料动态强度极限（）的大小关系，将式（2.3）写成以下三种形式：

①pS＜：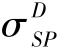

弹靶碰撞产生的冲击压力低于弹体材料强度极限（如钨弹侵彻铝靶），弹体无破损，忽略σSP的影响，式（2.3）可以简化为：

②pS≫：

弹靶碰撞产生的冲击压力远大于弹体材料强度极限（如射流侵彻钢靶），材料强度对穿甲效果影响微弱，材料可视为流体处理，则式（2.3）可简化为：

③pS＞

弹靶碰撞产生的冲击压力大于弹体材料强度极限，但程度有限（如钨弹侵彻钢靶），弹体的侵蚀、破损对穿甲效果影响显著，材料强度不可忽视，式（2.3）可简化为：

钨合金破片对有限厚钢靶穿甲中弹体发生严重的塑性变形、侵蚀及破裂对穿甲效果影响显著，属上述第③种情况。

对于，该量纲为1的数表征弹的惯性与靶的强度比值。午新民［25］（1999）通过试验获得了与相对厚度T/d的非线性函数关系。钱伟长［50］（1982）就塑性柱状弹的碰撞变形提出了与弹体变形后截面积的解析表达式：

式中，ρP为弹体密度；v0为弹体着靶速度；为弹体动态屈服强度；A为弹体变形后的截面积；A0为弹体初始截面积。由式（2.7）可得：

由式（2.8）可见，弹体撞击后，截面积改变量与着靶速度呈线性关系。对于球弹，弹体截面积与弹体直径成二次函数关系，则弹体直径改变量与着靶速度成二次函数关系。

弹体侵彻中，弹靶密度的高低是相对的，对于特定的弹靶系统，量纲为1的数ρv2/σy中，密度量的选择可针对弹体，也可针对靶体。对于不同材料的靶体，本书采用靶体临界贯穿损伤数，即临界贯穿条件下，靶体的惯性阻力与动态屈服强度之比）作为因变量来研究其与弹靶厚度的关系。根据霍-柯氏［125］（1960）提出的靶体发生塑性变形所需着靶速度表达式vP＝可见，靶体发生塑性变形破坏时，必有。因此，靶体临界贯穿损伤数必大于1。

对于中厚靶体，破片高速穿甲中所受的惯性阻力远远大于材料的变形阻力，在此，忽略材料应变率效应对动态屈服强度的影响，依据表2.4中实测的Q235A钢和2A12-T4铝静态屈服强度，通过A.C.Whiffin［126］（1948）的经验公式（2.9）和式（2.10）计算获得表2.6中的材料动态屈服强度。

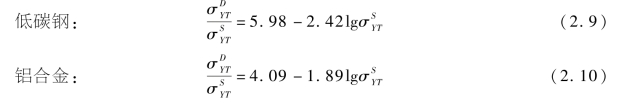
式中，为材料的动态、静态屈服强度，t/in2^[1]。

表2.6　Q235A钢、2A12-T4铝动态屈服强度

依据表2.5中的弹道极限值，通过计算获得同厚度（10 mm）Q235A钢、2A12铝两种金属靶在4种破片冲击下的靶体临界贯穿损伤数，如图2.21所示。

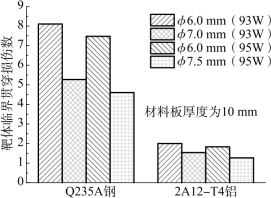
图2.21　两种金属靶的靶体临界贯穿损伤数

分析图2.21和图2.17可知，4种破片贯穿两种金属靶的临界比动能与两种金属靶在4种破片撞击下的靶体临界贯穿损伤数的对比关系具有一致性，均为φ6 mm（93W）最高，φ7.5 mm（95W）最低。可见，密度及力学性能几乎一样的破片贯穿同厚度金属靶，体积越小，所需的比动能越高，也对靶体产生更为严重的破坏，破片的撞击比动能决定了靶体的穿孔破坏程度。

分析获得靶体临界贯穿损伤数与靶体厚度的关系，如图2.22所示。由图2.22可见，靶体临界贯穿损伤数随着靶体厚度的增加而呈线性函数关系递增，对于不同尺寸破片，函数规律却有所不同。

图2.22　靶体临界贯穿损伤数与厚度的关系

分析获得不同厚度Q235A钢靶在4种破片撞击下，靶体临界贯穿损伤数与相对厚度的关系，如图2.23（a）所示。由图2.23（a）可见，靶体临界贯穿损伤数随靶体相对厚度的增加而呈线性函数关系递增，且不同尺寸破片函数关系基本相似。

图2.23　靶体临界贯穿损伤数与弹靶相对厚度的关系

（a）按破片类型区分显示；（b）整体显示

综合分析不同厚度Q235A钢靶在4种破片撞击下，靶体临界贯穿损伤数与相对厚度的关系，如图2.23（b）所示。分析图2.23（b）可见，在破片着靶速度段，靶体临界贯穿损伤数随弹靶相对厚度的增加而呈线性函数关系递增，即

式中，A、B为拟合系数，分别为18.54、-21.03（R2＝0.987）。