灰色关联度诊断法的优化方案

在工程机械液压系统故障诊断中，由于观测到的参数只是系统的部分技术特征，有的信息知之不准或无法知道，很难对系统的运行状态做全面、准确的描述。灰色系统理论是研究如何利用系统的已知信息去认识这个含有不可知信息系统的特性、状态和发展趋势的一门新理论。灰色关联度诊断法通过对灰色因素间的关联程度的分析，研究系统当前运行状态与“故障”与“正常”这两种参考状态特征间的相关性，从而确诊系统的运行工况。

1.灰色聚类诊断法

首先根据某液压元件的特征参数，建立两个参考模式向量：

正常状态：Y₁={y₁₁，y₁₂，…y_1n}

故障状态：Y₂={y₂₁，y₂₂，…，y_2n}

设该液压元件的实际参数向量为W，即待检状态，

W={w₁，w₂，…，w_n}

计算W与Y₁之间的关联度

其中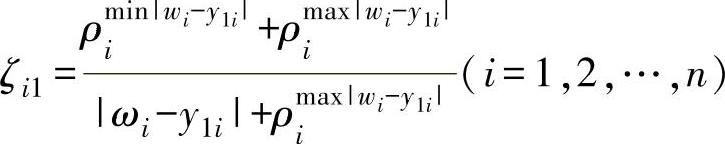

及W与Y₂之间的关联度

其中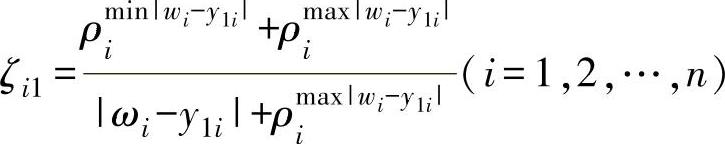

及W与Y₂之间的关联度

其中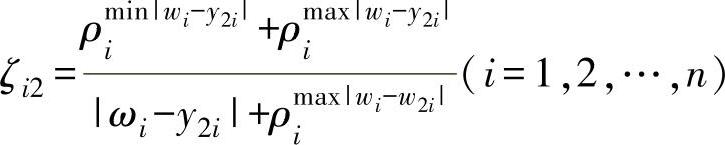

式中 ρ——分辨系数，ρ∈（0，1），通常取ρ=0.5。

其中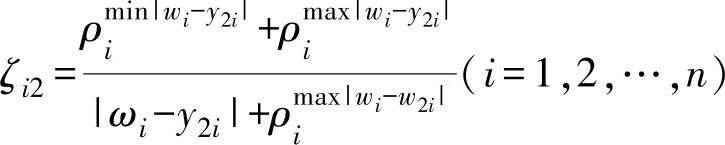

式中 ρ——分辨系数，ρ∈（0，1），通常取ρ=0.5。

2.最大关联度法

以Y={y₁，y₂}来表示某液压元件的参考运行状态（其中，y₁为故障状态，y₂为正常状态），并选取特征向量参数U={u₁，u₂，…，u_m}，经适当的数据处理，构造参考状态矩阵Y_u。

u₁u₂…u_m——特征参数

2.最大关联度法(www.xing528.com)

以Y={y₁，y₂}来表示某液压元件的参考运行状态（其中，y₁为故障状态，y₂为正常状态），并选取特征向量参数U={u₁，u₂，…，u_m}，经适当的数据处理，构造参考状态矩阵Y_u。

u₁u₂…u_m——特征参数

假设该元件有两种运行工况（w₁，w₂）需做状态识别，根据现场实测数据，构造待检状态参数矩阵W。即

u₁u₂…u_m——特征参数

假设该元件有两种运行工况（w₁，w₂）需做状态识别，根据现场实测数据，构造待检状态参数矩阵W。即

u₁u₂…u_m——特征参数

对Y_u与W进行AB型关联度分析，得AB型关联度矩阵R_ij（i=1，2；j=1，2）

R_ij=aR_Aij+bR_Bij

式中，a，b——权系数，a+b=1，a，b∈[0，1]，计算时可取a=b=0.5；

对Y_u与W进行AB型关联度分析，得AB型关联度矩阵R_ij（i=1，2；j=1，2）

R_ij=aR_Aij+bR_Bij

式中，a，b——权系数，a+b=1，a，b∈[0，1]，计算时可取a=b=0.5；

其中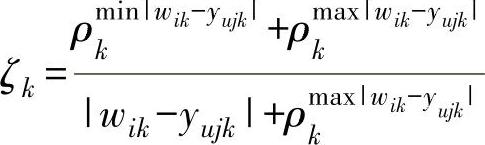

其中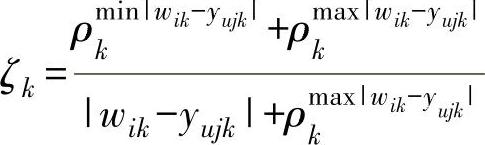

式中 ρ——分辨系数，常取ρ=0.5。

根据R中每一行的最大关联度所在列数，来判断待检状态w₁、w₂属于故障状态y₁还是正常工况y₂。

式中 ρ——分辨系数，常取ρ=0.5。

根据R中每一行的最大关联度所在列数，来判断待检状态w₁、w₂属于故障状态y₁还是正常工况y₂。