液力传动的流体力学基础

1.液体在工作轮中的几点假设条件

液体在工作轮中的运动，是十分复杂的空间运动。为了问题的研究、分析方便，可做如下假设；

1）运动的液体为理想液体，即液体是连续的、不可压缩的、无黏性的。

2）工作轮叶片无限多，形状相同，厚度无限小，因而液流被分成无限多的与曲线一致的流束。

3）在各条流束下，液流的流速均相等。

4）叶片系统对液体的作用，相当于对中间流束的作用。

由上述假设可知，液体在工作轮中的运动是轴对称的。即每一相应点的液体质点在工作轮中的运动轨迹相同、运动速度相等、流量对称。因此，只要研究其中的一条流速就可以体现液体的全部运动。

2.液体在工作轮中的运动

液体在旋转工作轮中的运动是一种复合的运动，各速度之间的关系可用速度三角形来表示。如图1-27a所示，任取一工作轮，假定工作轮的流道中充满了工作液体，当工作轮以角速度ω做顺时针方向旋转时，工作轮流道内的液体质点x的运动将由两种运动组成。一种是液体质点随工作轮旋转的圆周运动，也叫牵连运动。其速度用u表示，称为圆周运动速度，方向为圆周的切线方向。另一种是液体质点沿工作轮叶片的流动，称为相对运动。其运动速度用w表示，称为液体的相对速度，方向为叶片切线方向。而两种运动速度合成，即为液体质点x在工作轮中流动的绝对运动速度v。

绝对运动速度为

v=u+w （1-49）

在液力传动中，由于工作轮叶片对液流的作用，使液体质点在工作轮进出口处的速度发生变化。所以常用速度v、w、u组成的速度平行四边形来反映它们的液流速度矢量关系，并可简化为一个封闭的三角形来代替，即所谓的速度三角形，如图1-27b所示。用它来讨论液流速度变化。

图1-27 流束在叶片式工作轮中的变化

在速度三角形中，α角为绝对速度与圆周速度之间的夹角；β角为相对速度与圆周速度之间的夹角，下标“1”表示工作轮入口处的参数符号，“2”表示工作轮出口的参数符号。

为研究方便，在速度三角形中常将绝对速度v分解成两个互相垂直的分量v_m、v_u。

v_u——绝对速度在圆周速度方向的投影，称为圆周分速度。

v_m——绝对速度在轴面内（过工作轮轴线的剖面）的投影，称为轴面分速度。

速度三角形中各个速度的大小、方向以及相互之间的关系如下：

v_u=vcosα （1-50）

v_m=vsinα （1-51）

确定投影v_u的正负号规则，应和角速度ω相适应，因而从右向左为正，反之为负；投影v_m由叶轮中心向外为正，反之为负。

工作轮叶片通道任一点的圆速度u为

式中 r_t——工作轮叶片通道中任一点到轴心的距离（半径）（m）；

n——工作轮的转速（r/min）。

3.力矩方程式

将流体力学中的动量定律应用于液力变矩器，可以推导出工作轮叶片与油泵间相互作用力矩的关系式。

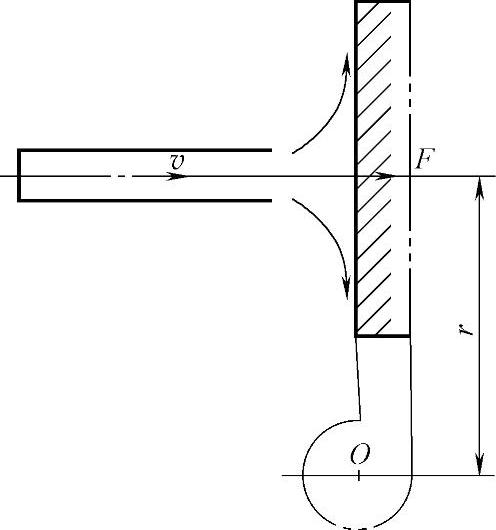
图1-28 液流冲击某一固定平面叶片的情况

液流的动量方程式为

由式（1-55）可计算出油液与固定平面之间的作用力。图1-28所示为液流冲击某一固定平面叶片的情况。

液流射向平面后受平面作用而改变了方向，则平面对液流的作用力为

F₁=ρq（cos90°-v）=-ρqv （1-56）

而液流对平面的作用力F与F₁的大小相等、方向相反，则

在力F的作用下，该平面叶片企图绕O点转动。若r为力F的作用半径，则转动力矩M为

M=Fr=ρqvr （1-58）

ρqvr称为液流对O点的动量矩。上述关系不仅适用于液流冲击某一平面叶片的情况，也适用于液流冲击或离开某一弯曲叶片的情况。如图1-29所示，假如液流从某一曲面叶片的一侧进入，而从另一侧流出，则：

弯曲叶片入口处的动量矩为-ρqvr（对O点顺时针为负）；弯曲叶片出口处的动量矩为ρqvr（对O点逆时针为正）；弯曲叶片所获得的转动力矩M_O为液流进入和流出弯曲叶片的动量矩之差，即

M_O=-ρqv₂r₂-ρqv₁r₁ （1-59）

整理得

M_O=-ρq（v₂r₂+v₁r₁） （1-60）

式中，负号表示曲面叶片绕O轴顺时针方向转动。

如果被冲击的物体本身也在运动，情况就有所不同。如图1-30所示，液体进入叶片的绝对速度为v₁，叶片本身也以圆周速度u在运动，所以液流相对叶片的速度为w₁。w₁的大小和方向由进口处的速度三角形来决定；液流离开叶片的相对速度为w₂，因叶片具有圆周速度u，则液流绝对速度v₂的大小和方向将由出口处的速度三角形来决定。

此时，液流对叶片的作用力F为

F=ρq（w₁cosβ₁-w₂cosβ₂） （1-61）

根据三角关系有

w₁cosβ₁=u-v₁cosα₁； w₂cosβ₂=u-v₂cosα₂ （1-62）所以有

F=ρq（v₂cosα₂-v₁cosα₁） （1-63）

同理，液流穿过旋转叶轮时对叶轮产生的力矩仍等于液流在叶轮入口和出口处的动量矩变化，即

M_O=-Fr=-ρq（v₂cosα₂r₂-V₁cosα₁r₁） （1-64）(www.xing528.com)

图1-29 液流射到固定曲面的情况

图1-30 液流射到运动曲面的情况

式中，负号表示叶轮顺时针转动。

根据式（1-50）得

v_2u=v₂cosα₂， v_1u=v₁cosα₁ （1-65）

则式（1-60）可写成

M_O=-ρq（v_2ur₂-v_1ur₁） （1-66）

因为所有叶片间的液流情况相同，若q表示整个工作轮的流量，M表示液流对所有工作轮叶片的力矩之和。根据作用力矩与反作用力矩大小相等、方向相反的原理，液流所受的力矩与上述的力矩之和大小相等、方向相反。

为方便起见，将式（1-60）等号右边加上正负号来表示液力传动的基本方程式，称为力矩方程式。即

M=±ρq（v_2ur₂-v_1ur₁） （1-67）

力矩方程式表明了液流流经工作轮时，液流与工作轮叶片间的相互作用的力矩关系。

4.相似理论与力矩方程

力矩方程式一般只做理论研究，用于定性地分析问题。实际上，由于液流流动极为复杂，因此很难确切地计算出它的特性。为弄清它的特性往往依靠试验及相似原理科学地把这些研究试验数据进行概括总结，用模型特性推算相似系列的液力传动特性，即实际计算中不直接应用力矩方程式，而是用相似理论导出所谓的力矩公式。

在流体力学中，把满足下面三个条件的液流叫作相似液流，相似液流具有相同的水力特性。

1）几何相似：两个液流对应尺寸成比例，对应角相等。

2）运动相似：两个几何相似的液流，对应点的速度三角形相似。

3）动力相似：几何相似且运动相似的液流，对应点作用着方向一致的同名力，力的大小成比例。

建立在这三个条件基础上研究液流相似问题的理论，称为相似理论。

实际上，完全的动力相似是不可能达到的。一般是按照所研究的性质，找出其主要的作用力。只要主要作用力满足动力相似，就可以认为该液流是相似的。

对于变矩器中的油液，上述三个条件可叙述如下：

几何相似：变矩器的过流通道对应尺寸成比例，对应角相等。几何相似的变矩器叫作同一系列的变矩器。

运动相似：同一系列的变矩器中，液流对应点的速度三角形相似。运动相似时也叫作相似工况下工作。

动力相似：同一系列变矩器在相似工况下工作时，油液对应点作用着方向一致、大小成比例的同名力时即为动力相似（力学相似）。

变矩器油液中的主要作用力是惯性力和黏性力。为了计算简单，通常忽略黏性力，据此可推导几个主要的关系式，其中就有所谓的力矩公式。

设有两个变矩器1（或为模型变矩器）和2（或为实物变矩器）呈力学相似，则根据相似条件，它们的泵轮间有

式中 D₁、r₁₂、r₁₁——变矩器1的有效直径、有效出口半径、有效进口半径；

D₂、r₂₂、r₂₁——变矩器2的有效直径、有效出口半径、有效进口半径。

同理有

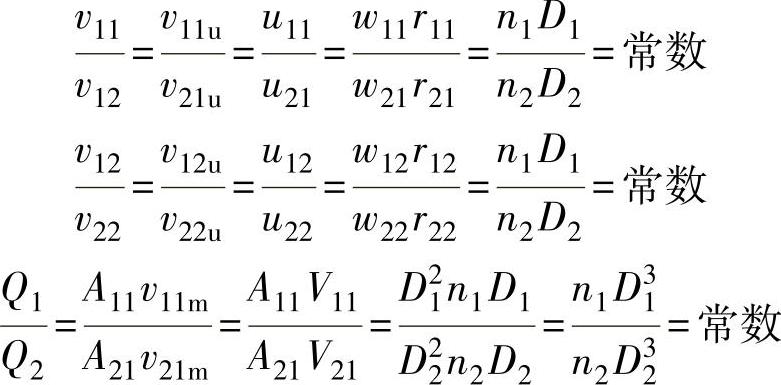
式中 A——泵轮进口过流断面面积；

v_m——绝对速度的径向分速度。

两变矩器力矩之比为

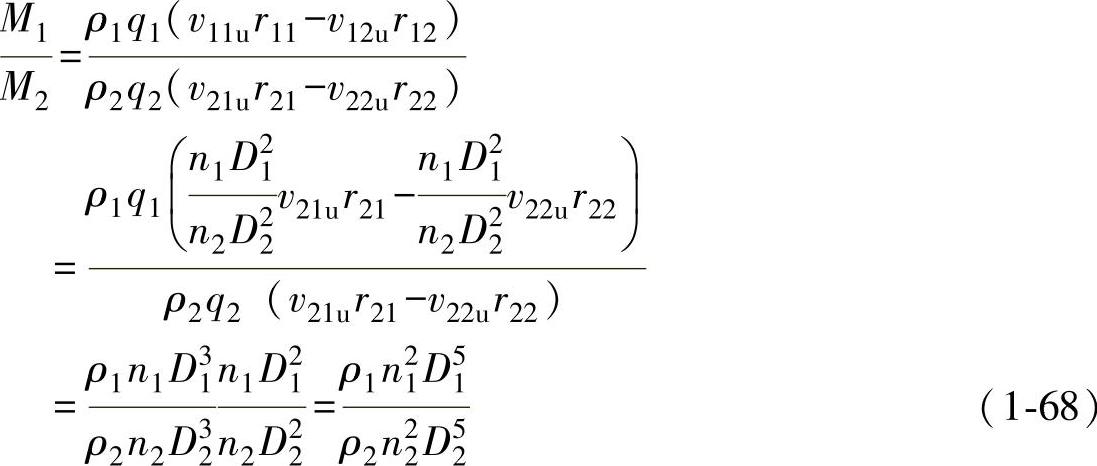
或写为

由式（1-69）可知，同一系列的变矩器，在相似工况下工作时，其泵轮的力矩M₁与油液的密度ρ、泵轮的转速n₁的平方、泵轮的有效直径D₁的五次方成比例。因此，泵轮的力矩的一般形式可以写为

M_B=λ₁ρn²₁D⁵₁ （1-70）

式中 λ₁——比例系数，称为泵轮的力矩系数，其值由试验确定，同一系列的变矩器，在相似工况下工作时，λ₁等于常数；

ρ₁、ρ₂、ρ——变矩器工作介质油的密度，由于是同一油液，故ρ₁=ρ₂=ρ。

同理，也可以得到同一系列变矩器涡轮的力矩公式，即

M_T=λ₂ρn²₂D⁵₂ （1-71）

式（1-68）～式（1-71）中 q——流量；

ρ——油液的密度；

n₁、n₂——泵轮、涡轮的转速；

D₁、D₂——泵轮、涡轮的有效直径；

M_B、M_T——泵轮、涡轮所传递的力矩；

λ₁、λ₂——泵轮、涡轮的力矩系数。

根据上述泵轮与涡轮的力矩公式，同一变矩器内变矩系数K可写为