液体流动的基本规律解析

液压系统中液压油在不断流动，流动着的液体在液压系统的不同位置上的流动状态不同，表达液体流动状态的参数，如流速、压力、能量及动量等在不断变化。然而，各参数的变化以及它们之间的关系都有一定的规律。本小节将研究这些规律，以进一步认识整个液压系统，解决液压技术中的问题。

1.流动液体的连续性原理

能量守恒是自然界的客观规律，不可压缩液体的流动过程也遵守能量守恒定律。在流体力学中这个规律是用称为连续性方程的数学形式来表达的。

如图1-9所示，其中不可压缩流体做定常流动的连续性方程为

v₁A₁=v₂A₂ （1-20）

由于通流截面是任意取的，则有

q=v₁A₁=v₂A₂=v₃A₃=…=v_nA_n=常数 （1-21）

式中 v₁、v₂——流管通流截面A₁及A₂上的平均流速。

式（1-21）表明，通过流管内任一通流截面上的流量q相等，当流量一定时，任一通流截面上的通流面积与流速成反比。由此可知，任一通流断面上的平均流速为

v_i=q/Ai

图1-9 液体的微小流束连续性流动示意图

2.伯努利方程

能量守恒是自然界的客观规律，流动液体也遵守能量守恒定律，这个规律是用伯努利方程的数学形式来表达的。伯努利方程是一个能量方程，掌握这一物理意义是十分重要的。

（1）理想液体微小流束的伯努利方程 为研究的方便，一般将液体作为没有黏性摩擦力的理想液体来处理，如图1-10所示，伯努利方程为

式中 p/（ρg）——单位质量液体所具有的压力能，称为比压能，或称压力水头；

Z₁——单位质量液体所具有的势能，称为比位能，或称位置水头；

v²/（2g）——单位质量液体所具有的动能，称为比动能，或称速度水头。

图1-10 液流能量方程关系转换图

对伯努利方程可做如下的理解：

1）伯努利方程式是一个能量方程式，它表明在空间各相应通流断面处流通液体的能量守恒规律。

2）理想液体的伯努利方程只适用于重力作用下的理想液体做定常流动的情况。(www.xing528.com)

3）任一微小流束都对应一个确定的伯努利方程式，即对于不同的微小流束，它们的常量值不同。

伯努利方程的物理意义：在密封管道内做定常流动的理想液体在任意一个通流断面上具有三种形式的能量，即压力能、势能和动能。三种能量的总和是一个恒定的常量，而且三种能量之间是可以相互转换的，即在不同的通流断面上，同一种能量的值会是不同的，但各断面上的总能量值都是相同的。

（2）实际液体微小流束的伯努利方程 由于液体存在着黏性，其黏性力在起作用，并表示为对液体流动的阻力，实际液体的流动要克服这些阻力，表示为机械能的消耗和损失。因此，当液体流动时，液流的总能量或总比能在不断地减少。所以，实际液体微小流束的伯努利方程为

式中 u₁、u₂——通流截面上的流速；

h_w——两通流截面间流动的液体单位质量的能量损失。

（3）实际液体总流的伯努利方程

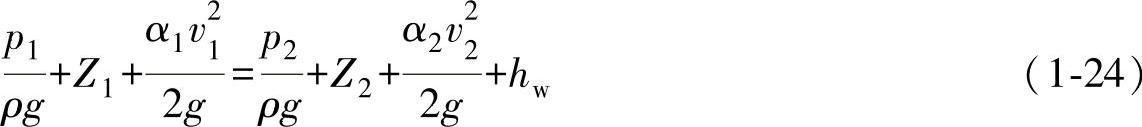
式中 α₁、α₂——因流速不均匀引起的动能修正系数。

伯努利方程的适用条件如下：

1）稳定流动的不可压缩液体，即密度为常数。

2）液体所受质量力只有重力，忽略惯性力的影响。

3）所选择的两个通流截面必须在同一个连续流动的流场中是渐变流（即流线近于平行线，有效截面近于平面），而不考虑两截面间的流动状况。

图1-11 流动液体的动量方程

3.流动液体的动量方程

动量方程是动量定理在流体力学中的具体应用。流动液体的动量方程是流体力学的基本方程之一，它是研究液体运动时作用在液体上的外力与其动量的变化之间的关系。在液压传动中，在计算液流作用在固体壁面上的力时，应用动量方程去解决就比较方便。

如图1-11所示，流动液体的动量方程（推导过程可参考其他资料）为

F=ρq（β₂u₂-β₁u₁） （1-25）

式中 q——液体流量；

β₁、β₂——动量修正系数。

它是一个矢量表达式，液体对固体壁面的作用力F与液体所受外力F′大小相等方向相反。