静止液体的基本性质：探究与分析

液压传动是以液体作为工作介质进行能量传递的，因此要研究液体处于相对平衡状态下的力学规律及其实际应用。所谓相对平衡是指液体内部各质点间没有相对运动，至于液体本身完全可以和容器一起如同刚体一样做各种运动。因此，液体在相对平衡状态下不呈现黏性，不存在切应力，只有法向的压应力，即静压力。本节主要讨论液体的平衡规律、压强分布规律以及液体对物体壁面的作用力。

1.液体静压力及其特性

作用在液体上的力有两种类型：一种是质量力，另一种是表面力。

质量力作用在液体所有质点上，它的大小与质量成正比，属于这种力的有重力、惯性力等。单位质量液体受到的质量力称为单位质量力，在数值上等于重力加速度。

表面力作用于所研究液体的表面上，如法向力、切向力。表面力可以是其他物体（例如活塞、大气层）作用在液体上的力，也可以是一部分液体间作用在另一部分液体上的力。对于液体整体来说，其他物体作用在液体上的力属于外力，而液体间的作用力属于内力。由于理想液体质点间的内聚力很小，因此液体不能抵抗拉力或切向力，即使是微小的拉力或切向力都会使液体发生流动。因为静止液体不存在质点间的相对运动，也就不存在拉力或切向力，所以静止液体只能承受压力。

所谓静压力是指静止液体单位面积上所受的法向力，用p表示。

液体内某质点处的法向力ΔF对其微小面积ΔA的极限称为压力p，即

若法向力均匀地作用在面积A上，则压力表示为

p=F/A （1-14）

式中 A——液体有效作用面积；

F——液体有效作用面积A上所受的法向力。

静压力具有下述两个重要特征：

1）液体静压力垂直于作用面，其方向与该面的内法线方向一致。

2）静止液体中，任何一点所受到的各方向的静压力都相等。

2.液体静力学方程

静止液体内部受力情况可用图1-3来说明。设容器中装满液体，在任意一点A处取一微小面积dA，该点距液面深度为h，距坐标原点高度为Z，容器液平面距坐标原点的Z向距离为Z₀。为了求得任意一点A的压力，可取hdA这个液柱为分离体（见图1-3b）。

根据静压力的特性，作用于这个液柱上的力在各方向都呈平衡，现求各作用力在Z方向的平衡方程。微小液柱顶面上的作用力为p₀dA（方向向下），液柱本身的重力G=ρghdA（方向向下），液柱底面对液柱的作用力为pdA（方向向上），则平衡方程为

pdA=p₀dA+ρghdA

图1-3 静压力的分布规律

a）液体内部受力 b）微元液柱

故

p=p₀+ρgh （1-15）

为了更清晰地说明静压力的分布规律，将式（1-15）按坐标Z变换一下，即以h=Z₀-Z代入式（1-15）整理后得

p+ρgZ=p₀+ρgZ₀=常量 （1-16）

式（1-16）是液体静力学基本方程的另一种形式。其中，Z实质上表示A点的单位质量液体的位能。设A点液体质点的质量为m，重力为mg，如果质点从A点下降到基准水平面，其重力所做的功为mgZ。因此，A点处的液体质点具有位置势能mgZ，单位质量液体的位能就是mgZ/mg=Z，Z又常称作位置水头。而p/ρg表示A点单位质量液体的压力能，常称为压力水头。

由以上分析及式（1-15）可知，静止液体中任一点都有单位质量液体的位能和压力能，即具有两部分能量，而且各点的总能量之和为一常量。由此得出如下结论：

1）静止液体中任一点的压力均由两部分组成，即液面上的表面压力p₀和液体自重而引起的对该点的压力ρgh。

2）静止液体内的压力随液体距液面的深度变化呈线性规律分布，且在同一深度上各点的压力相等，压力相等的所有点组成的面为等压面，很显然，在重力作用下静止液体的等压面为一个平面。

3）可通过下述三种方式使液面产生压力p₀：

①通过固体壁面（如活塞）使液面产生压力。

②通过气体使液面产生压力。

③通过不同质的液体使液面产生压力。

3.压力的表示方法及单位

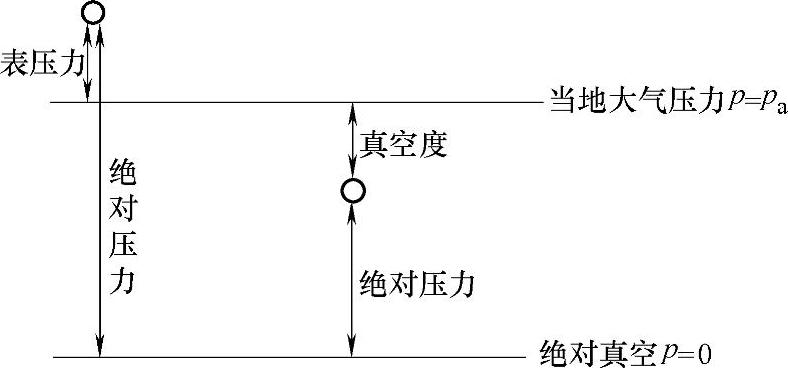
液压系统中的压力就是指压强。液体压力通常有绝对压力、相对压力（表压力）、真空度三种表示方法。因为在地球表面上，一切物体都受大气压力的作用，而且是自成平衡的，即大多数测压仪表在大气压下并不动作，这时它所表示的压力值为零，因此它们测出的压力是高于大气压力的那部分压力。也就是说，它是相对于大气压（即以大气压为基准零值时）所测量到的一种压力，因此称它为相对压力或表压力。另一种是以绝对真空为基准零值时所测得的压力，称它为绝对压力。当绝对压力低于大气压时，习惯上称为出现真空。因此，某点的绝对压力比大气压小的那部分数值叫作该点的真空度。如某点的绝对压力为4.052×10⁴Pa（0.4atm），则该点的真空度为0.6078×10⁴Pa（0.6atm）。绝对压力、表压力（相对压力）和真空度的关系如图1-4所示。

由图1-4可知，绝对压力总是正值，表压力则可正可负，负的表压力就是真空度，如真空度为4.052×10⁴Pa（0.4atm），其表压力为-4.052×10⁴Pa（-0.4atm）。如图1-5所示，把下端开口，上端具有阀门的玻璃管插入密度为ρ的液体中，如果在上端抽出一部分封入的空气，使管内压力低于大气压力，则在外界的大气压力p_a的作用下，管内液体将上升至h₀，这时管内液面压力为p₀，由流体静力学基本公式可知：p_a=p₀+ρgh₀。显然，ρgh₀就是管内液

(www.xing528.com)

图1-4 绝对压力、表压力和真空度的关系

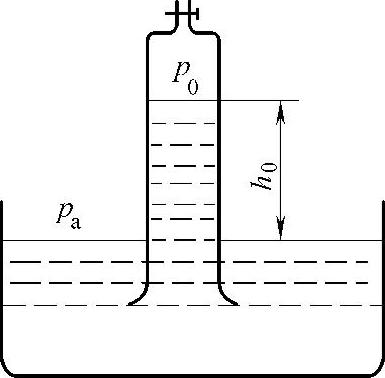
图1-5 真空度

面压力p₀不足大气压力的部分，因此它就是管内液面上的真空度。由此可见，真空度的大小往往可以用液柱高度h₀=（p_a-p₀）/（ρg）来表示。在理论上，当p₀等于零时，即管中呈绝对真空时，h₀达到最大值，设为h_0maxr，在标准大气压下，

h_0maxr=p_a/（ρg）=101325/（9.8066ρ）=10332/ρ

因为水的密度为10³kg/m³，汞的密度为13.6×10³kg/m³，所以

h_0maxr=10.33mH₂O或h_0maxr=760mmHg

即理论上在标准大气压下的最大真空度可达10.33mH₂O或760mmHg。

根据上述归纳如下：

绝对压力=大气压力+表压力

表压力=绝对压力-大气压力

真空度=大气压力-绝对压力

压力的单位为Pa，1Pa=1N/m²。由于此单位很小，工程上使用不便，因此常采用它的倍数单位MPa，1MPa=10⁶Pa。

4.帕斯卡原理

密封容器内的静止液体，当边界上的压力p₀发生变化，如增加Δp时，则容器内任意一点的压力将增加同一数值Δp。也就是说，在密封容器内施加于静止液体任一点的压力将以等值传到液体内各点。这就是帕斯卡原理或静压传递原理。

在液压传动系统中，通常是外力产生的压力要比液体自重所产生的压力大得多。因此，可把式（1-15）中的ρgh项略去，而认为静止液体内部各点的压力处处相等。

图1-6 静压传递原理应用实例

根据帕斯卡原理和静压力的特性，液压传动不仅可以进行力的传递，而且还能将力放大和改变力的方向。图1-6所示为应用帕斯卡原理推导压力与负载关系的实例，图中垂直液压缸（负载缸）的截面积为A₁，水平液压缸截面积为A₂，两个活塞上的外作用力分别为F₁、F₂，则缸内压力分别为p₁=F₁/A₁，p₂=F₂/A₂。由于两缸充满液体且互相连接，根据帕斯卡原理有p₁=p₂。因此有

F₁=F₂A₁/A₂ （1-17）

式（1-17）表明，只要A₁/A₂足够大，用很小的力F₁就可产生很大的力F₂。液压千斤顶和水压机就是按此原理制成的。

如果垂直液压缸的活塞上没有负载，即F₁=0，则当略去活塞自重及其他阻力时，不论怎样推动水平液压缸的活塞也不能在液体中形成压力。这说明液压系统中的压力是由外界负载决定的，这是液压传动的一个基本概念。

5.液压静压力对固体壁面的作用力

在液压传动中，略去液体自重产生的压力，液体中各点的静压力是均匀分布的，且垂直作用于受压表面。因此，当承受压力的表面为平面时，液体对该平面的总作用力F为液体的压力p与受压面积A的乘积，其方向与该平面相垂直。如果液压油作用在直径为d的柱塞上，则有F=pA=pπd²/4。

当承受压力的表面为曲面时，由于压力总是垂直于承受压力的表面，所以作用在曲面上各点的力不平行但相等。要计算曲面上的总作用力，必须明确要计算哪个方向上的力。

图1-7所示为液压缸筒受力分析图。设缸筒半径为r，长度为l，求液压力作用在右壁部x方向的力F_x。在缸筒上取一微小窄条，其面积为dA=ldS=lrdθ，液压油作用在这微小面积上的力dF在x方向的投影为

dF_x=dFcosθ=pdAcosθ=plrcosθdθ

在液压缸筒右半壁上x方向的总作用力为

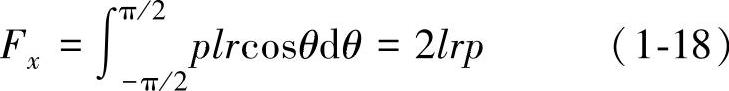
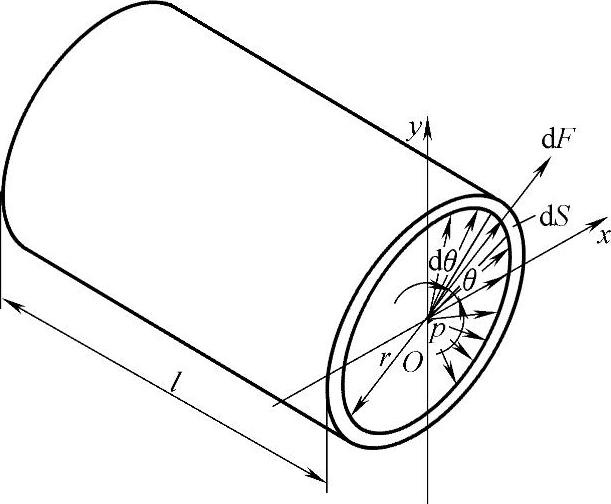
图1-7 液压缸筒受力分析图

式中 2lr——曲面在x方向的投影面积。由此可得出结论，作用在曲面上的液压力在某一方向上的分力等于静压力与曲面在该方向投影面积的乘积。这一结论对任意曲面都适用。

图1-8所示为球面和锥面所受液压力分析图。要计算出球面和锥面在垂直方向的受力F，只要先计算出曲面在垂直方向的投影面积A，然后再与压力p相乘，即

F=pA=pπd²/4 （1-19）

式中 d——承压部分曲面投影圆的直径。

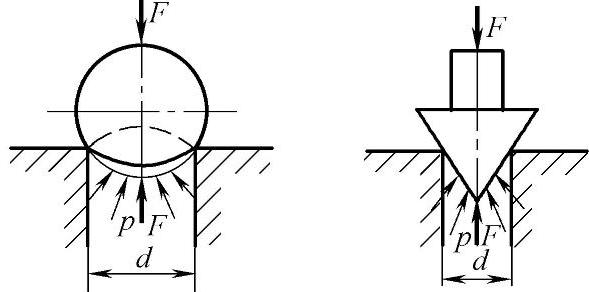
图1-8 球面和锥面所受液压力分析图