实用性研究：深入探讨10.2.3

人与机器人的交互过程中，情感因素的引入能够使人机交互更加自然和谐。因此，完整的人工情感模型的建立是首要解决的问题。基于情感能量理论基础，本部分首先，提出了心境自发转移和刺激转移模型。其次，结合情绪自发转移的马尔可夫链模型和刺激转移的HMM模型，将心境和情绪的自发转移和刺激转移过程统一在一个框架下。最后，将完整的人工情感模型软件化并应用于儿童玩伴机器人上，在接受非结构化环境与用户的信息输入后，个性化的情感软件模块产生输出，实现针对儿童用户的玩伴机器人个性化交互，并通过应用验证了该模型的有效性。

1.个性化情感模型研究基础

由于情感可划分为心境（Mood）和情绪（Emotion）2个广泛的分类，因此其转移过程在不同条件下可分为4种，如图10-12所示。

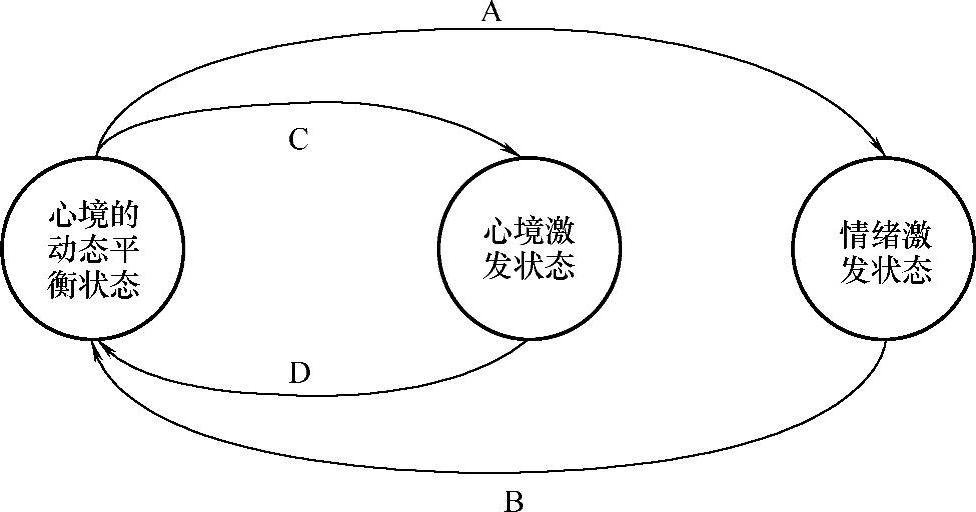
图10-12 心境与情绪状态转移图

图10-12展现了4个过程：

1）情绪状态刺激转移：在外部事件刺激下，情感状态由心境的动态平衡状态移到某种激发水平的情绪激发状态，由A线表示；

2）情绪状态自发转移：当外界刺激作用结束后，某种情绪状态将在一定时间内由激发状态自发地转移到心境的动态平衡状态，由B线表示；

3）心境状态刺激转移：在某种特异性外部事件刺激下，心境状态在以心境的动态平衡状态为中心的一定范围内发生转移，由C线表示；

4）心境状态自发转移：在外界刺激消失后，某种心境激发状态将在一定时间内自发地向心境动态平衡状态转移，由D线表示。

综合上述，4个过程分别对应玩伴机器人中的4个个性化情感模型：

1）情绪状态刺激转移过程的随机过程模型；

2）情绪状态自发转移过程的马尔可夫链模型；

3）心境状态刺激转移过程的控制论模型；

4）心境状态自发转移过程的动态平衡模型。4个模型相辅相成，在4个过程中共同作用。它们具有一致的理论基础。在心理学中心理能量观点的基础上，滕少冬提出了情感能量的概念，成为建立个性化情感模型的出发点和基础。

心理能量就是推动个体进行各种心理活动以及行为的能力，用E表示。它有2种基本表现形式：

1）自由的心理能量E_η；

2）受约束的心理能量E_λ。它们满足：

E_λ=λE，E_η=ηE，η＋λ=1 （10-54）

则情感能量可以用下式表示：

E_p=E_η＋γE_λ=（1－λ）E＋γλE=（1－λ＋γλ）E （10-55）

同时，设E_p^t=［E_p^t1，E_p^t2，…，E_p^tN］为t时刻实际表现出的情感强度的绝对分布向量。此向量的求解在后面介绍。

根据巴甫洛夫高级神经学说，由于生理的原因，人的大脑神经细胞在兴奋与抑制2种状态之间按一定的生理机制呈周期性的变化，伴随着这种变化，个体的意识状态也将在清醒与不清醒之间进行转化，从而使得情感能量E_p在表达时，呈现出周期性的变化。把由

E_p^α=αE_p=α（1－λ＋γλ）E （10-56）

定义的情感能量称为生理性激活的情感能量，它是实际用于表现情绪的情感能量，称α（0≤α≤1）为生理性唤醒度。把由式

E^β_p=βE_p=β（1－λ＋γλ） E（10-57）

定义的情感能量称为生理性抑制的情感能量，它是用于表现心境的情感能量，称β（0≤β≤1）为生理性抑制度。且有：

α＋β=1 （10-58）

α和β主要由生理机制进行周期性的调节，即“生物钟”的调节。另外，α和β还会受到某些外界刺激的干扰。心理能量以及情感能量的各种形式以及转化关系如图10-13所示。

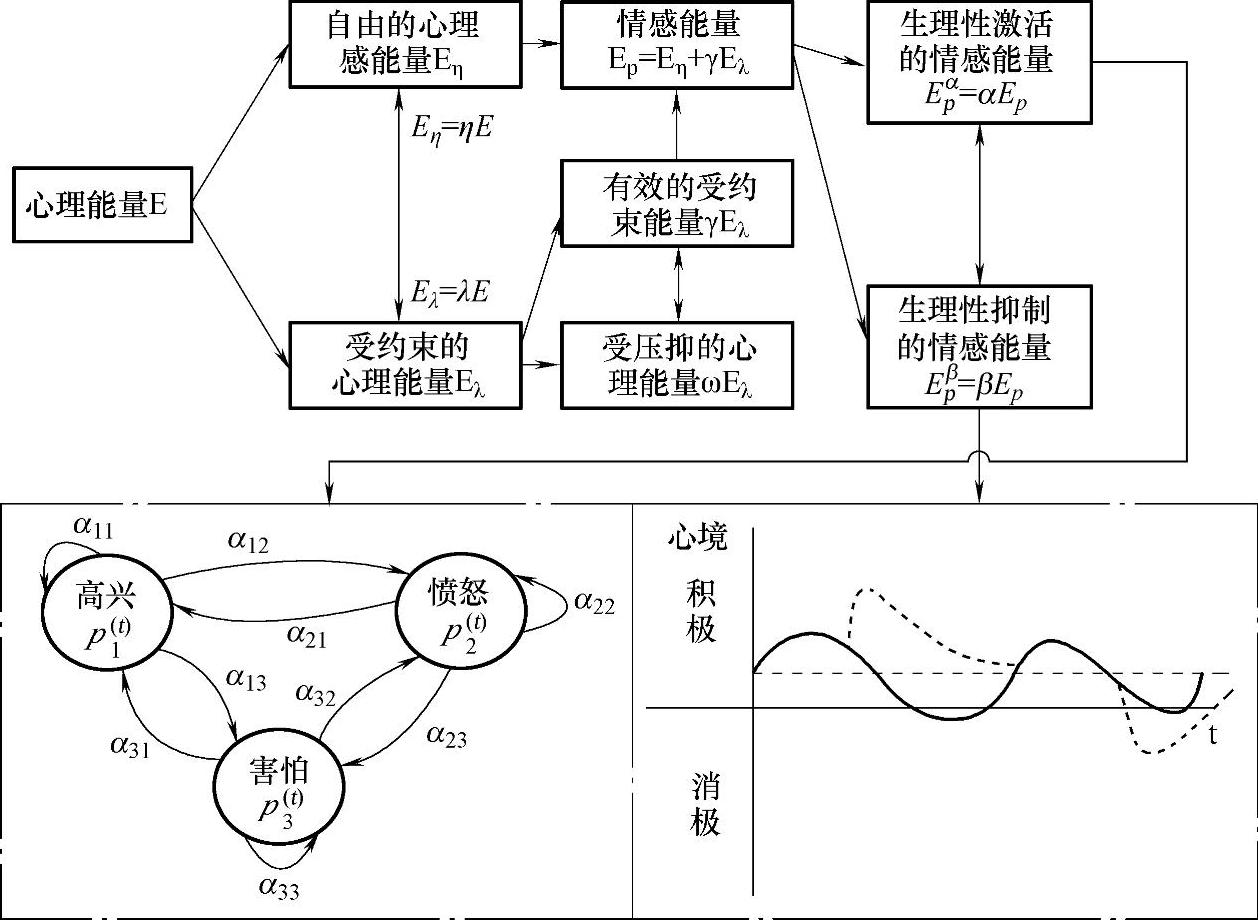
图10-13 情感能量的各种形式以及转化关系图

从动力心理学的观点来看，个体产生各种不同情绪的过程，实际上就是激活的情感能量E_p^α在不同情绪状态之间的动态分配过程，图10-13的左下半部分反映了这样的关系。

E_p^αt=［E_p^α1t，E_p^α2t，…，E_p^αNt］为t时刻实际表现的情绪强度绝对分布向量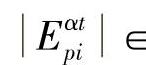，[0，1]，i∈｛1，2，…，N｝是激活的情感能量在各维度的能量值分量。根据情感能量守恒定律，有下式成立：

生理性抑制的情感能量E^β_p在积极心境与消极心境之间变化，由其引起的心境强度变化如图10-13的右下半部分所示。

相应的，称E^β_pt=［E^β_pt1，E^β_p2t，…，E^β_pNt］为t时刻实际表现的心境强度绝对分布向量，并设与积极情绪对应的心境个数是m，与消极情绪对应的心境个数是n，则m＋n=N。其中：

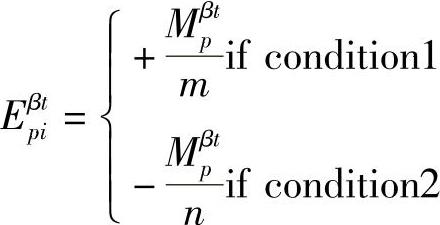，condition1是指分量i属于积极心境；condition2是指分量i属于消极心境。M^β_pt为t时刻的心境强度，其计算方法在后面介绍。

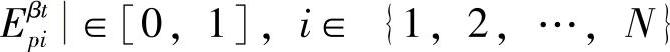是生理性抑制情感能量在各维度上的能量值分量。根据情感能量守恒定律，有下式成立：

设0≤Epαit≤1，－1≤Eβpit≤1，并定义了3种运算：＋，－，Δ。其中，＋，－运算和实数域R中的加法和减法运算相似，但加法不具有交换律性质。即：∀E_p^αit∈[0，1]，E^β_pit∈[－1，1]时，E_p^αit＋E^β_pit≠E^β_pti＋E_p^αit。Δ运算定义为

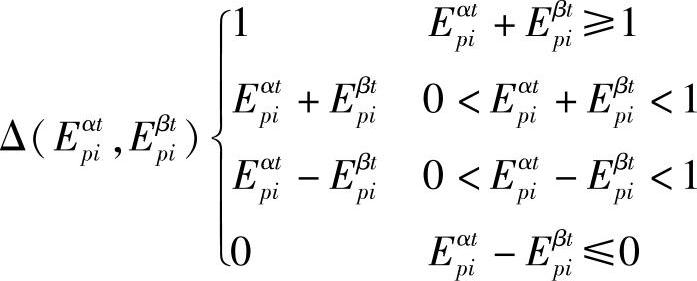
由于情感可划分为心境和情绪，则t时刻的情感强度定义为：

E_p^t=［E_p^t1，E_p^t2，…，E_p^tN］=Δ（［E_pаt₁，E_pа2^t，…，E_pаN^t］，［E^β_pt1，E^β_p2t，…，E^β_pNt］） （10-61）

=［Δ（E_pаt₁，E^β_pt1），Δ（E_pа2^t，E^β_p2t），…，Δ（E_pаN^t，E^β_pNt）］

由式（10-61）可知，t时刻的情感强度与心境强度和情绪强度有关，根据上述的4个转移过程，它们的求解在下面将分别进行介绍。

2.心境自发转移

Larsen认为，平均的、稳定的心境特征并没有真实地反映个体的心境特征，心境随着时间的推移，其性质（好或不好）以及强度（弱或极度）是变化的。Parkinson认为与心境动态性有关的理论有动态平衡理论、社会牵引理论和非线性动态理论。并把影响心境的因素分为三类，其中之一来自个体内源性因素，如人格和生理因素。这里的心境自发转移模型就是从个体内源性角度建立的。

（1）人格对心境的影响

对不同的人而言，所体验到的心境可能不同，换句话说存在着个体差异，这种差异来自于相对稳定的人格。同时，人格特征又决定了心境水平和心境变化性，心境自发地在相对稳定的心境特征水平附近波动，我们用C表示由人格决定的心境特征水平，如图10-10右下部分的横线描述。由多种因素的影响，C在积极消极分界线左右一定范围内变动，假设C∈[－1，＋1]。

（2）生理因素对心境的影响

个体的生理性周期变化会引起心境在积极与消极之间随时间t的变化而有所波动。

1）心境的昼夜波动：根据Watson的研究，积极心境在一天中的趋势是早上较低，而后在一天中的某个时间上升到最大值；接着逐渐下降，在晚上达到最低。此过程用一余弦函数σcos（ω₁·t）表示。其中，σ是心境的昼夜影响因子，2π／ω₁是心境的昼夜波动周期。

2）心境的周变化：根据Larsen与Kasimatis的研究发现，具有正弦波的7天间隔解释了日常心境的变化。积极心境在周五达到顶峰，在周二处于最低。此过程用一正弦函数ζsin（ω₂·t）表示。其中，ζ是心境的周变化影响因子，2π／ω₂是心境的周变化周期。

3）心境的月变化：主要是针对女性的月经周期循环的心境效应，因此，此项对心境的影响是个性化的，具有性别差异。此过程用一正弦函数τsin（ω₃·t）表示。其中，τ是心境的月变化影响因子，2π／ω₃是心境的月变化周期。

4）心境的季节变化：Watson认为在理论上积极情感应该有一个显著的季节模式。春季的积极心境水平较高，接着在夏季和秋季逐渐下降，最终达到冬季的最低点。此过程用一正弦函数υsin（ω₄·t）表示。其中，υ是心境的季节变化影响因子，2π／ω₄是心境的季节变化周期。

根据以上周期性变化，有σ，ζ，τ，υ∈［0，1］，σ＋ζ＋τ＋υ=1，ω₁=7ω₂=30ω₃=365ω₄。对于男性用户，取σ=0.7，ζ=0.2，τ=0，υ=0.1；对于女性用户，取σ=0.5，ζ=0.2，τ=0.2，υ=0.1。由于心境的变化缓慢且某一心境常常能持续一段时间，因此，这里每隔1h计算一次心境量值，心境的昼夜波动模型中，周期取24h，则ω₁=2π／24。

人格和生理因素对心境的动态变化共同产生影响，设心境的人格影响因子为ψ，心境的生理因素影响因子为ξ，且有：

ψ∈（0，1），ξ∈（0，1），ψ＋ξ=1 （10-62）

建立的心境自发转移模型为

M^β_pt=ξ·［σcos（ω₁·t）＋ζsin（ω₂·t）＋τsin（ω₃·t）＋υsin（ω₄·t）］＋ψ·C （10-63）

M^β_pt动态变化范围的确定：

因为，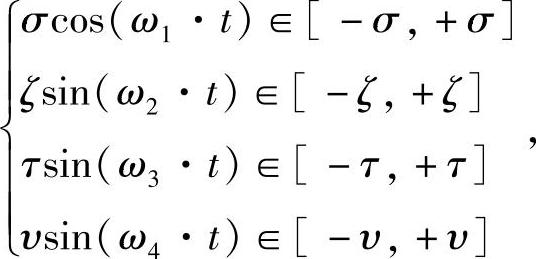

所以，

[σcos（ω₁·t）＋ζsin（ω₂·t）＋τsin（ω₃·t）＋υsin（ω₄·t）]

∈[（－σ－ζ－τ－υ），（＋σ＋ζ＋τ＋υ）]=[－（σ＋ζ＋τ＋υ），（σ＋ζ＋τ＋υ）]=[－1，1](www.xing528.com)

因为，C∈[－1，＋1]

所以，

M^β_pt∈[（－ξ－ψ），（ξ＋ψ）]=[－（ξ＋ψ），（ξ＋ψ）]=[－1，＋1] （10-64）

这里取ψ=0.5，ξ=0.5。

以上参数中，ω_i，i∈｛1，2，3，4｝取值较大时，相应的生理性周期变化引起的心境随着时间t的波动周期越小，即心境变化性越强。

3.心境刺激转移

在外部因素事件和情境刺激下，心境和情绪都受到影响，但其变化过程是有区别的：第一，持续时间上的差别；第二，相对强度上的差别；第三，信号功能上的差异。如前所述，对于情绪受到刺激后的变化过程，利用HMM这个双重随机过程来构造情绪状态刺激转移过程的情感模型，用HMM的前向和后向算法来模拟情绪在外界刺激下的变化规律，这一方法在后面将会介绍；对于心境受到刺激后的变化过程，则采用控制论的调整策略进行研究。

Larsen提出应将控制理论应用到心境调节的动态过程中。根据此观点对心境的刺激转移过程建模。

根据已有研究，心境对刺激的反应强度是略微平缓的，一阶惯性环节更适合描述。

定义心境的刺激转移模型为

其中，T称为心境转移时间常数，它是表征心境发生转移惯性的一个重要参数。有研究发现，女性可能比男性更容易受情绪传染或影响，因此，T参数也是男女性别差异对心境的影响参数之一，是个性化参数。后面将会介绍此参数对心境激发子过程的影响。E_event（t）是外源性因素（如，工作方式、生活事件、家中变故等）对心境的影响强度。

心境的刺激转移过程分为两2个子过程。

（1）心境激发子过程

该子过程与一个零状态响应过程类似。假设心境在t时刻受某一外源性因素激发时，心境强度初值为M^β_pt0∈[－1，＋1]，则事件影响强度为

在此条件下，求解式（10-65）表示的心境刺激转移模型。

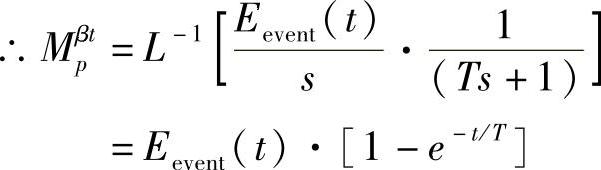
其中，L［·］，L^－1［·］分别为拉普拉斯变换和反变换。

根据心理学中情绪反应的时间动力性基本概念，可以定义心境中相应的概念。

称T_s为心境反应调节时间，T_s≈4T。这个参数表达了心境从初始强度M^β_pt0变化到－0.98或＋0.98（－1或＋1的±2％）的最短时间。

称T_d为心境反应延迟时间，T_d≈0.69T。这个参数表达了心境从初始强度M^β_pt0第一次达到E_event（t）×50％所需的时间。

称T_r为心境反应上升时间，T_r≈2.20T。此参数表达了心境从强度M^β_pt0＋E_event（t）×10％第一次上升达到M^β_pt0＋E_event（t）×90％所需时间（event是积极情绪事件），或从强度M^β_pt0＋E event（t）×10％第一次下降达到M^β_pt0＋E_event（t）×90％所需时间（event是消极情绪事件）。

根据上述的三个定义，可以看到心境反应调节时间的快慢，心境反应延迟时间和心境反应上升时间的长短，包含了重要的个体差异信息。这三个值都与心境转移时间常数T有关。因此，T参数是男女性别差异对心境产生影响的参数之一，是个性化参数，其大小对心境激发子过程是有影响的。

图10-14a是当T=0.5和T=0.9，E_event（t）=1时，心境激发子过程。从图中可以看出，心境反应调节时间、心境反应延迟时间和心境反应上升时间均不同，反映了男女性别差异对心境的影响。

心境强度M^β_pt在某一外源性因素的持续激发下不断变大，表现出了事件的影响随时间的积累作用。但其变化率却不断变小，即影响随时间变小，表明了心境在某一特定时间刺激下，越来越不敏感，对此事件的发生变得麻木，如图10-14b所示。

（2）心境衰减子过程

该子过程与一个零输入响应过程类似，出现在心境激发子过程之后。假设在t时刻外源性因素对心境的影响消失E_event（t）=0，消失时的心境强度初值为M^β_pt0∈[－1，＋1]。

在此条件下，求解式（10-65）表示的心境刺激转移模型。

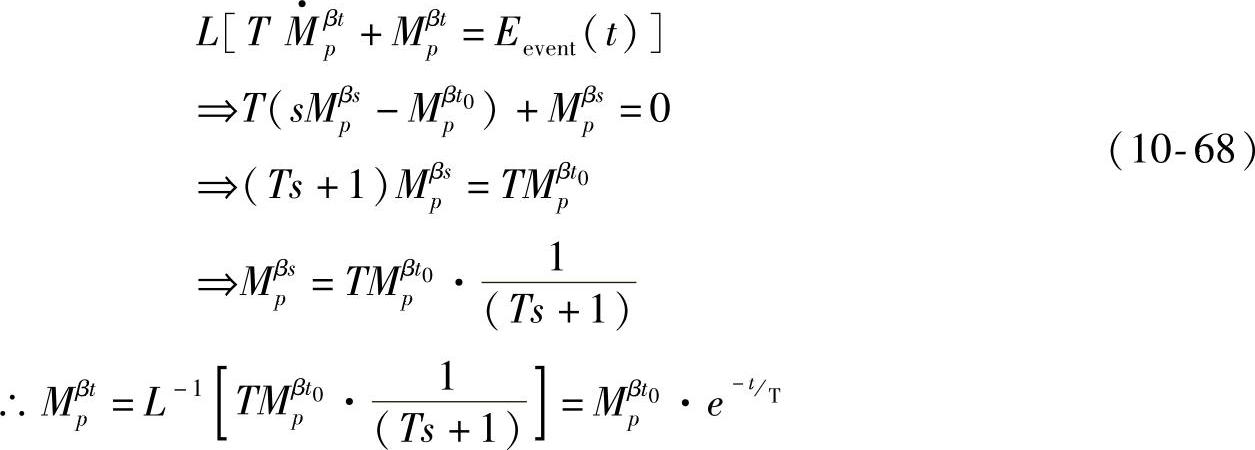
其中，L［·］，L^－1［·］分别是拉普拉斯变换和反变换。

为了便于计算机实现心境刺激转移模型，需要求解微分方程式（10-65）的差分方程形式。

根据式（10-65），有

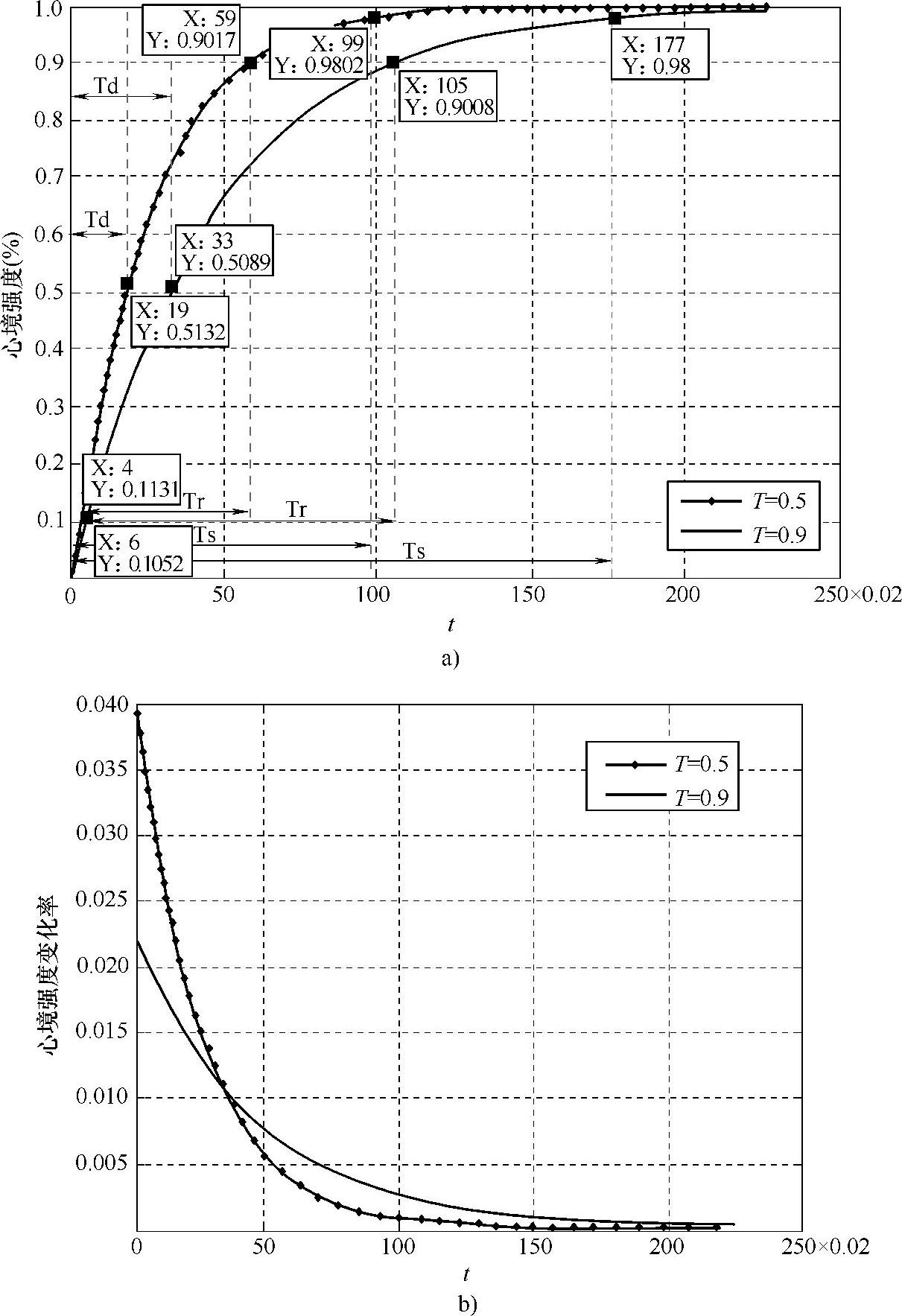
图10-14 心境激发子过程与强度变化率

a）心境激发子过程 b）强度变化率

根据欧拉法，可得：

其中，h称为步长，是计算心境强度的间隔时间，这里取h=0.02。

这种微分方程差分化，可以为人工心理模型在计算机上的应用带来方便，但也会带来一定误差，见表10-2和表10-3。

表10-2 差分化后的误差（心境激发子过程）

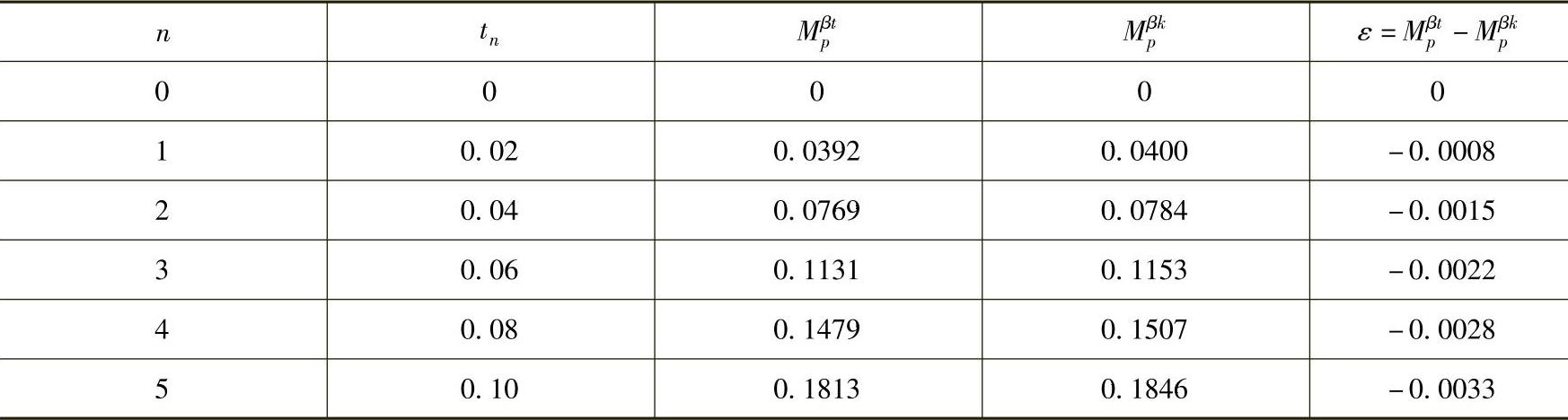
表10-3 差分化后的误差（心境衰减子过程）

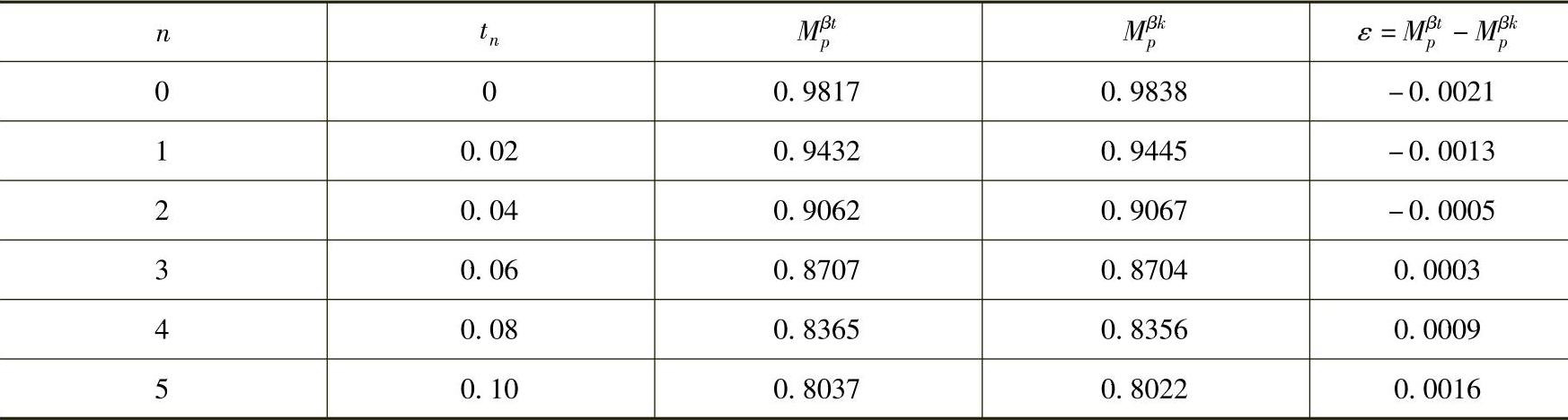
从表10-2和表10-3中可以看出，微分方程差分化后的误差为10^－3数量级，因此，仍采用差分的方法计算t时刻的情感强度，以利于情感计算的计算机实现。

4.针对特定用户的个性化情感

（1）完整的情感模型与情感滤波器

如前所述，在概率空间的基础上，可将情绪的变化过程看成一个随机过程，并进一步用马尔可夫链来描述情绪状态自发转移过程，进而给出基本方程以及计算方法。

实验中，以儿童玩伴机器人为实验平台，通过应用来验证模型的有效性。情感的发生通常都是混合的。儿童玩伴机器人在t时刻究竟处于那种情绪状态，可由E_p^αt中的各个分量的相对大小来确定。这里取情感维度中最大强度值对应的情感状态为需要表达的情感。

以上的情绪状态刺激转移模型、情绪状态自发转移模型、心境状态刺激转移模型、心境状态自发转移模型和情感滤波器，共同组成了一个完整的人工情感模型体系。

（2）个性化人工情感软件

基于上述理论，开发了一个针对特定用户的机器人个性化情感模型软件，如图10-15所示。

此软件应用于儿童玩伴机器人中，在用户与其对话、触摸、动作等交互方式的激励信息下，通过情感软件模块，产生个性化的输出，例如，控制机器人产生表情，如图10-16所示，实现个性化的交互。

5.结论

以情感能量为出发点，从个体内源性因素角度建立心境自发转移模型，从控制论的角度建立心境刺激转移模型。由于是从情感能量为出发点进行推演，为所提出的心境模型与情绪模型的结合创造了条件。为此，把心境、情绪四个模型统一到一个框架下，并进行软件化，开发了个性化人工情感软件系统，并将其应用于机器人情感控制方面。

人格和生理因素影响心境的自发转移过程，心境转移时间常数T也影响到刺激转移过程。通过调整模型中的参数，可以实现具有个体差异性的情感表达。以儿童玩伴机器人为实验平台，通过应用来验证模型的有效性。

本章所提出的心境模型以及开发的软件系统，可用于服务机器人、家用机器人等需要个性化服务的人机交互领域。其中，模型参数的合理选取与模型应用领域的拓展也有待进一步深入研究。

图10-15 人工情感软件

图10-16 情感控制机器人产生表情