研究个体情绪差异性

在情绪状态自发转移马尔可夫模型中，针对参数的调整是否会给个体情绪差异带来影响，以及影响的程度等有关个体情绪区分聚类的问题，提出了基于度量多元尺度分析理论的个体人工情绪差异性研究方法。通过不相似度矩阵计算内积矩阵，再应用主成分因素分析法，便可得到个体属性重构矩阵，在低维上展现个体情绪差异。试验结果可以用来指导模型参数的选取，并为实验的有效性提供了数学验证的依据。

根据基本方程（4），情绪状态自发转过程，即个体的情绪自发转移差异，取决于矩阵A，因此，参数θ和的确定，是对个体差异研究的关键。基于多元尺度分析，依次研究以下三个问题：1）参数θ和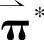的变化是否一定引起个体情绪自发转移差异；2）参数的变化引起什么样的个体情绪差异；3）情绪状态初值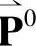的影响。下面分别加以详述。

1.对问题1的分析

上述情感状态自发转移的马尔可夫链模型中，情绪强度p_iΔ是情绪变化的一个重要度量。情绪强度定义为

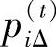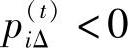并把称为某一时刻t（t≥0）的情绪强度。当时，情绪i处于激发状态；时，情绪i处于抑制状态；，情绪i处于平衡状态。但p_i（Δ^t）只是一个情绪变化的静态特征，要动态的反应个体情绪差异，则要计算情绪强度变化率向量，其中第i维情绪强度变化率Δp_i（Δ^t）为

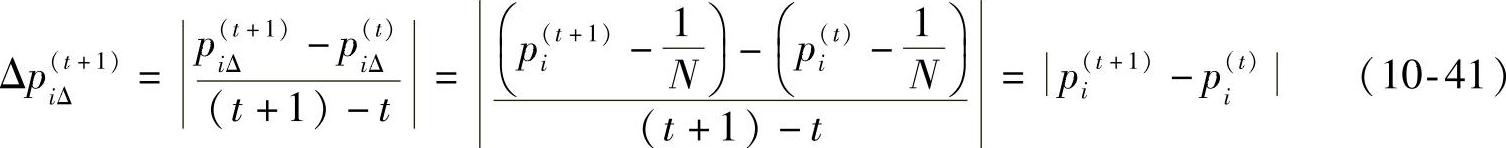
设情绪强度变化率向量在确定时刻T的值记为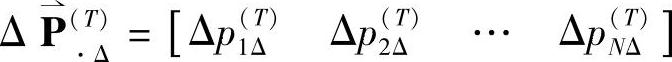，取T=5；情绪自发转移过程中的最大情绪强度变化率向量为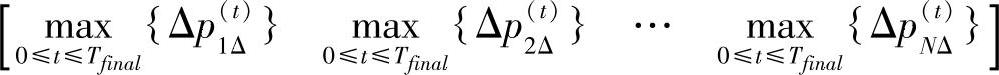，平均情绪强度变化率向量为MEANΔ，T_finɑl=50是情绪自发转移过程的最大时长。

在情绪自发转移过程中，个体情绪差异可以用、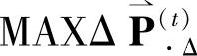和Δ^三个向量组成一个维度为3N的行向量来区分。即：个体i的属性向量为。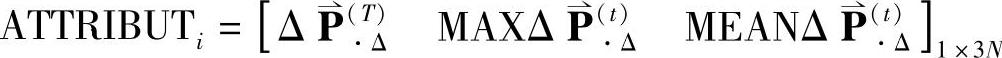

针对问题1，假设参数θ和中有且仅有一个参数发生变化，研究该参数对给个体差异变化带来的影响。由于i∈{1，2，…，N}线性相关，所以仅讨论θ、π₁^∗和π₂^∗的变化组合就可以了。他们的变化组合见表10-1。

表10-1参数θ和的组合

表10-1中，I（Increasement）表示该数值增大，D（Decreasement）表示该数值减小，U（Unchanged）表示该数值不变。由于组合中存在重复，因此θ、π₁^∗和π₂^∗的最终变化组合为L=7种，即研究7个差异个体。结合前面所述的个体的属性向量ATTRIBUT_ii∈{1，2，…，7}，可以建立个体属性矩阵为

ATTRIBUT=［ATTRIBUT₁ATTRIBUT₂…ATTRIBUT₇］′。

这里取情绪的维度N=3，则ATTRIBUT_i是一个9维行向量。根据度量多元尺度分析理论，在个体属性矩阵的基础上，构建不相似度矩阵Δ_L×L。Δ中的元素δ_ij为

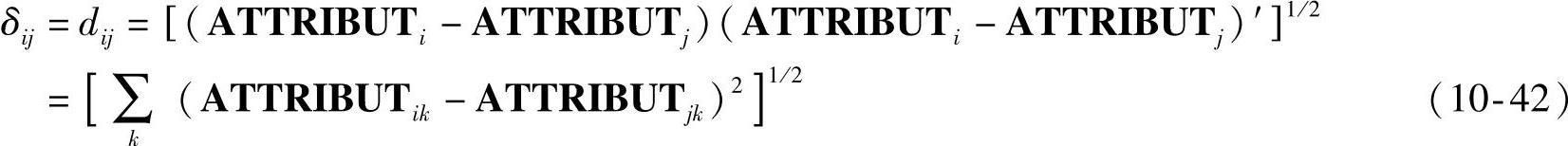
再计算内积矩阵Γ，其元素γ_ij为

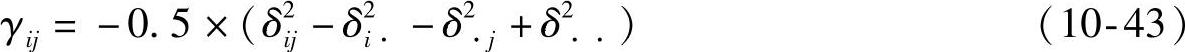
其中，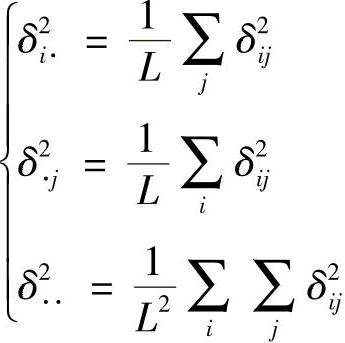

把个体属性矩阵在低维空间上的重构矩阵记为（M＜3N）。其表示的个体不相似度矩阵记为D，则根据度量多元尺度分析理论，Δ与D在某种意义上近似。且有：

求解式（10-44）可在低维空间上得到个体属性重构矩阵，即个体差异可以在低维空间被表示出。

同时，还可求出个体属性重构矩阵第j维对应的特征值λ_j：

其中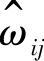，是的元素值。试验中得到的一组特征值随维度变化曲线如图10-8所示。

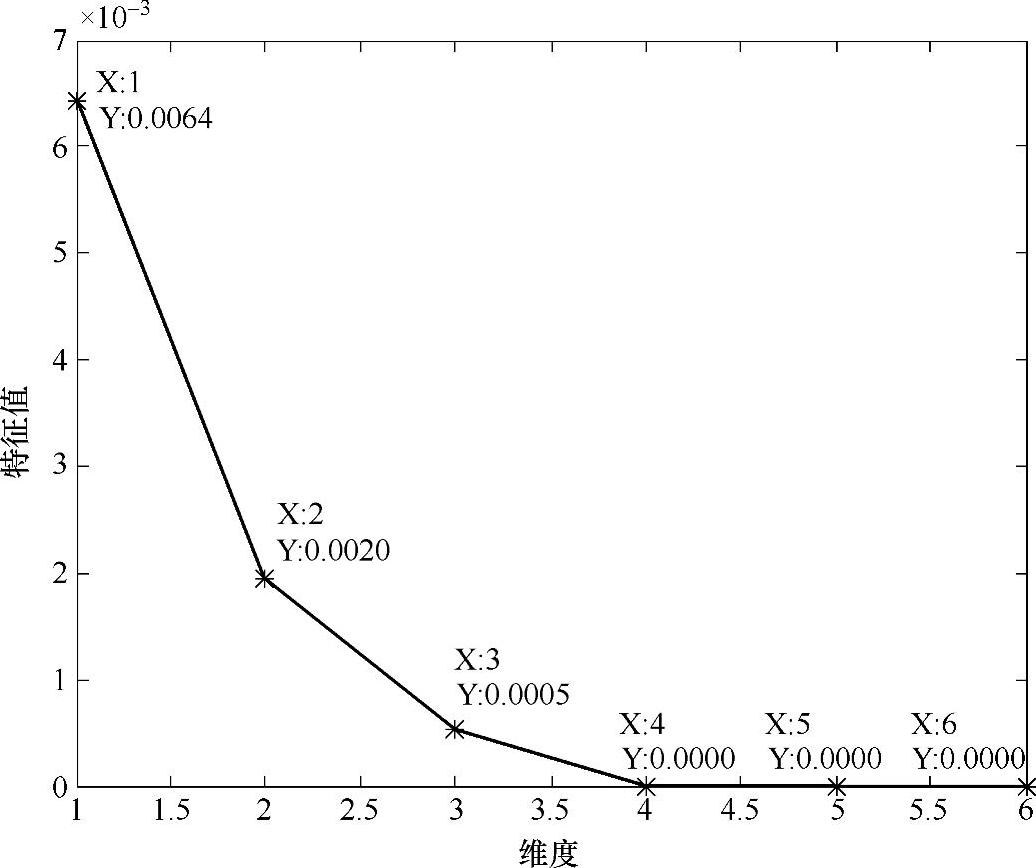
图10-8 特征值随维度变化曲线

根据图10-8，个体属性向量ATTRIBUT_i可以由原始的9维降到3维，而几乎不失真的加以表示。由于当维度为3时，特征值已经较小，因此，还可以进一步降到2维空间来表示个体差异。个体属性在2维空间的重构如图10-9所示。

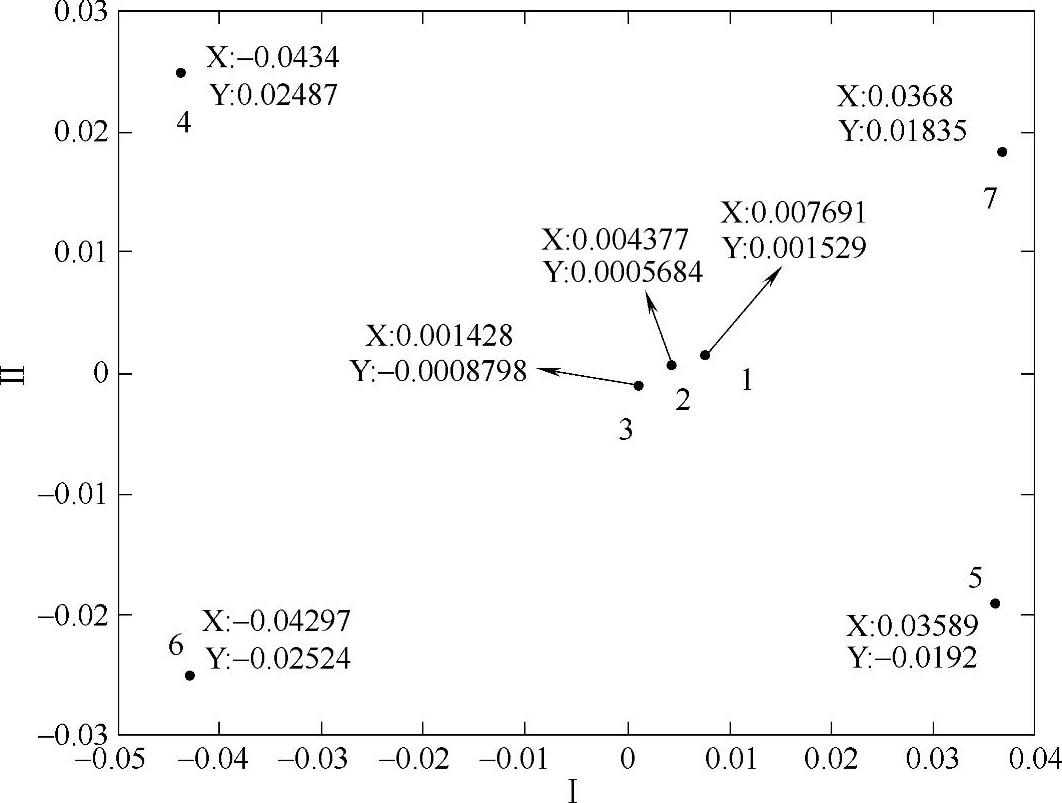
图10-9 T=5时个体属性重构图(www.xing528.com)

图10-9中的数字是与表10-1参数最终组合数序号相对应的。从图中可以看出，点1、2和3（分别对应于θ值的I、U和D的三种取值）之间的距离较近，说明θ值的变化只能引起个体情绪自发转移的少许差异，即改变θ对于个体情绪自发转移的差异性贡献较小；点4、5、6和7（分别对应于π_1∗和π_2∗值的I和D的各两种取值）间的距离较远，说明π_1∗和π_2∗值的变化能够引起个体情绪自发转移的较大差异，即改变π_1∗或π_2∗对于个体情绪自发转移的差异性贡献较大。

2.对问题2的分析

对于问题2，由于θ值的变化只引起个体情绪自发转移的少许差异，可以忽略，因此，仅讨论参数π_1∗和π_2∗值的变化引起何种个体情绪差异，即只讨论点4、5、6和7。

图10-10中，维度Ⅰ代表情绪强度变化率向量的第一个维度，维度Ⅱ代表情绪强度变化率向量的第二个维度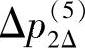。点4和点7在维度Ⅰ上有较大差距，在维度Ⅱ上差距不大；点4和点6则相反。其余点类似，他们的相互关系如图10-10所示。

下面结合点4、点6和点7讨论出现这种情况的原因。

根据式（10-4）和（10-41）

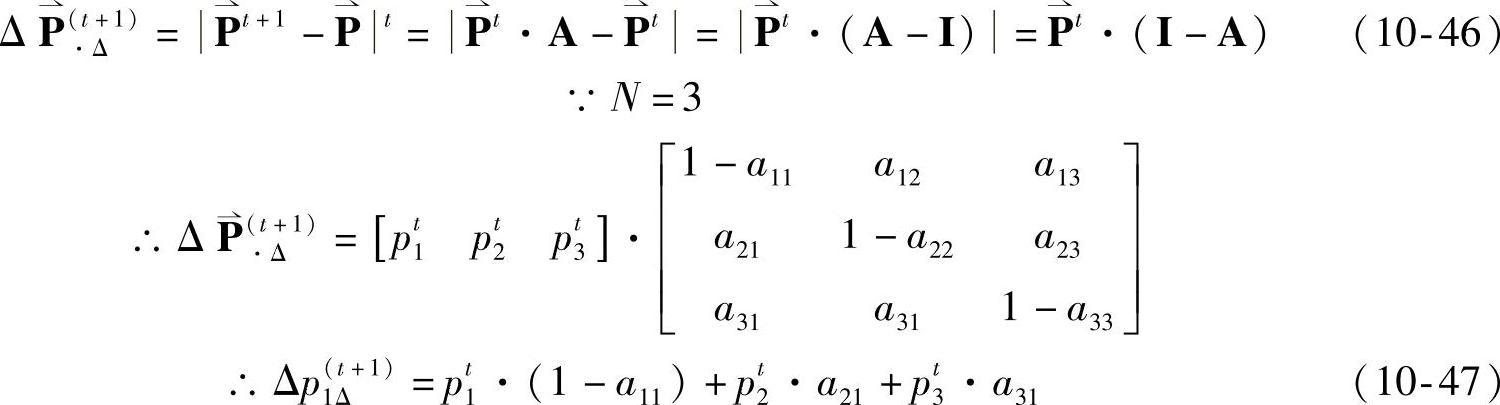
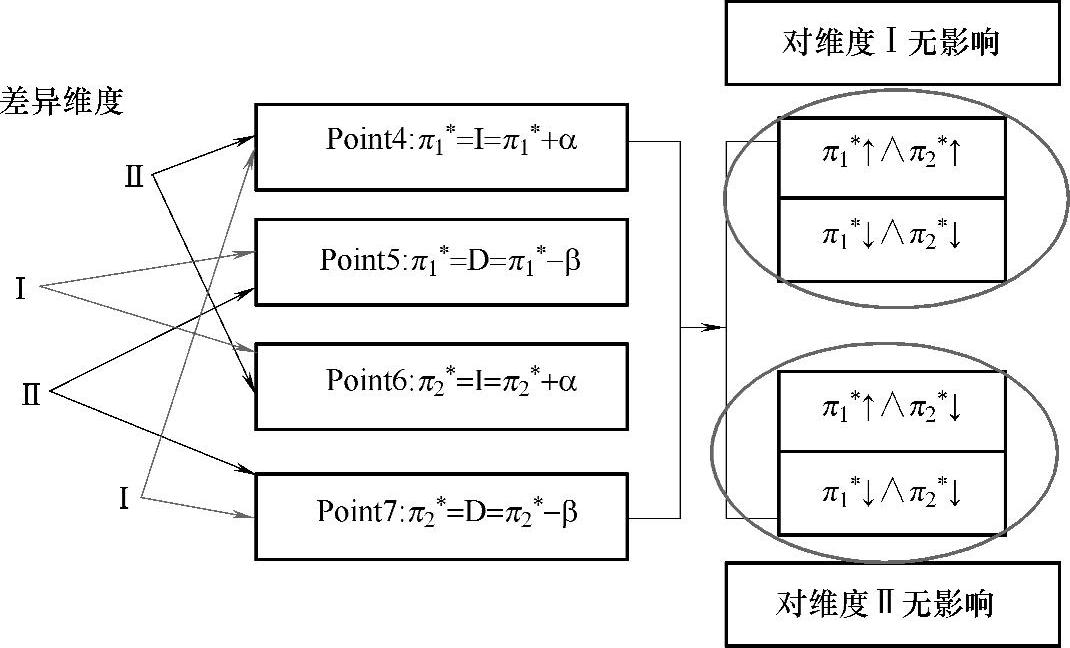
图10-10 参数调整对个体情绪差异在不同维度上的影响

a）对于表10.1的组合4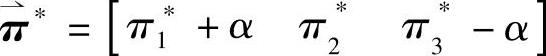，。由式（10-47）得，

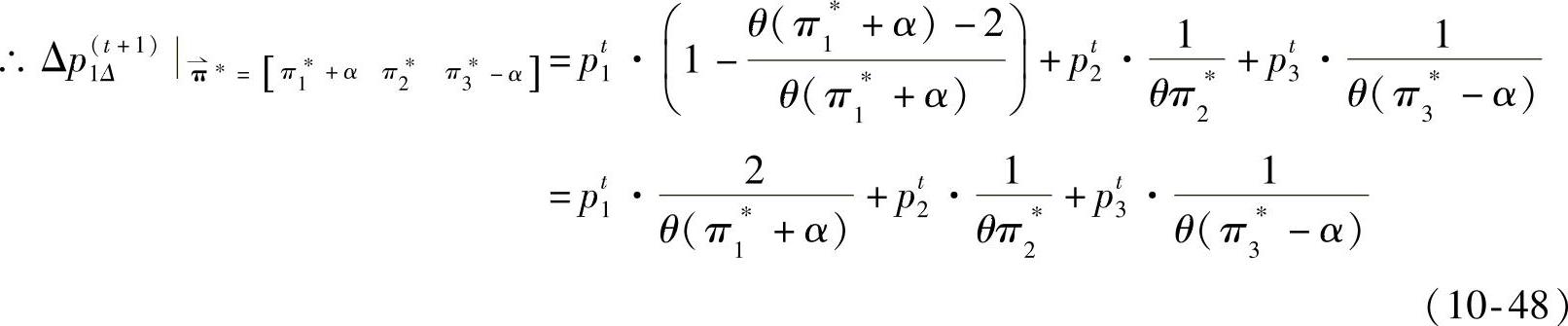
b）对于表10-1的组合6，。由式（10-47）得，

c）对于表10-1的组合7，。由式（10-47）得，

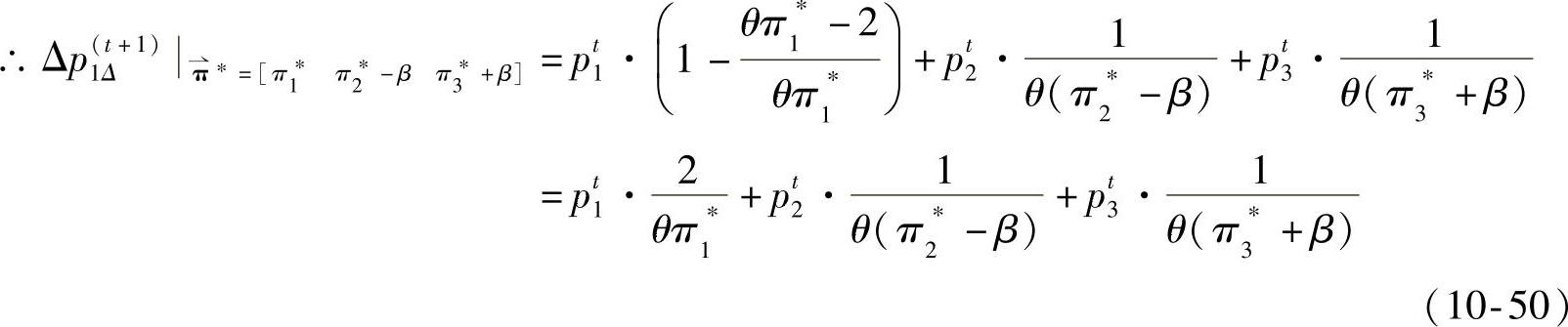
设π₁^∗=π₂^∗=π₃^∗=π^∗_·，根据式（10-48）（10-49），可得点4和点6在维度Ⅰ上的差距为

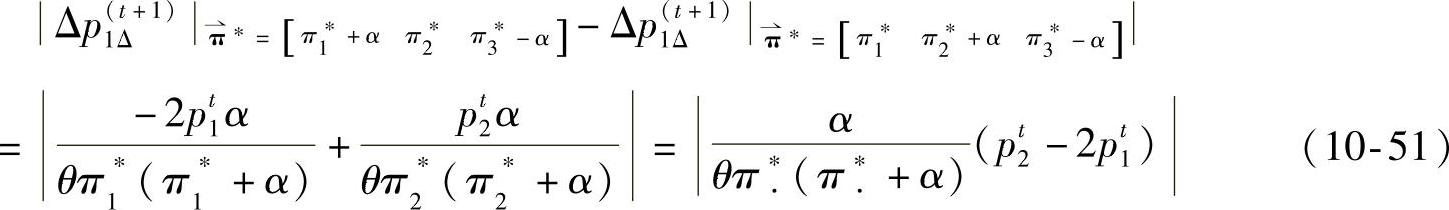
点4和点7在维度Ⅰ上的差距为

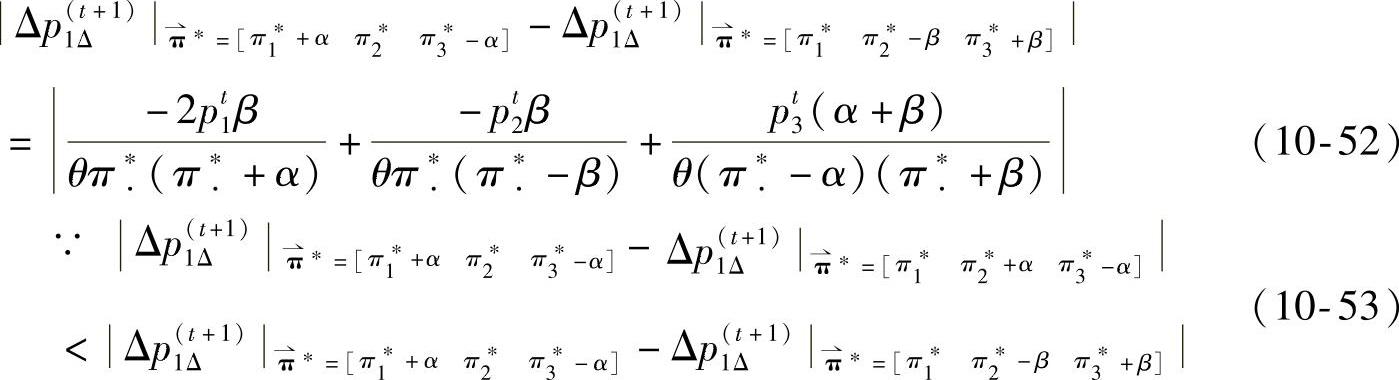
所以，点4和点6在维度Ⅰ上的差距小于点4和点7在维度Ⅰ上的差距。

可以看出，以上推导与确定时刻T的选取无关，图10-11中的“·”是T=21时的个体属性重构图。可以看出，确定时刻改变后，重构效果未变，说明上述结论具有代表性。

图10-11 T=21时，情绪状态初值改变后的个体属性重构图

综上，当参数π₁^∗和π₂^∗分别同向增大或减小时，引起个体情绪差异在情绪强度变化率向量第一个维度上的变化较小；反之，当参数π₁^∗和π₂^∗分别异向增大或减小时，引起个体情绪差异在情绪强度变化率向量第一个维度上的变化较大。

3.对问题3的分析

对于情绪状态初值⇀P⁰的影响，仅进行了5次试验。改变情绪状态初值，个体属性重构图也几乎未发生大的变化。图10-11中“·”是其中的一次重构效果。说明在情绪状态自发转移过程中，情绪状态初值的设定对个体情绪差异没有较大影响。这与常识是符合的，因为，个体的情绪差异是内在的、本质的，是不随初始情绪状态变化的。

4.结论

通常认为情感模型中的参数调整是影响模型输出变化的诱因，但这种调整是否一定能够引起个体情绪差异，以及对个体情绪差异影响的程度是值得探讨的。本部分针对情绪状态自发转移马尔可夫模型，研究了不同参数代表的个体情绪差异。结果表明，θ值的变化只能引起个体情绪自发转移的少许差异，π_∗值的变化能够引起个体情绪自发转移的较大差异。参数π₁^∗和π^∗₂分别同向增大或减小时，引起个体情绪差异在情绪强度变化率向量第一个维度上的变化较小；反之，当参数π_1∗和π_2∗分别异向增大或减小时，引起个体情绪差异在情绪强度变化率向量第一个维度上的变化较大。在情绪状态自发转移过程中，情绪状态初值的设定对个体情绪差异影响不大。