研究普适性的重要性

针对现有的隐马尔可夫情感模型仅能产生基本情绪的问题，提出了一种改进的模型，使其能够产生复合情绪。首先，放宽已有理论的假设条件，使得某种刺激可以引发多种基本情绪，并且两种基本情绪状态的强度可以同时增大，提高模型的普适性；其次在引入辅助矩阵和可变阈值后，实现了情感模型的复合情绪生成。并通过仿真试验，验证了该模型的有效性。

1.HMM情感模型的推广

基于上述模型的假设3，得到M=N的结论，即基本情绪总数与刺激类型总数是相等的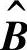，阵为一方阵，这样某种刺激就会确定性地只引发某一种基本情绪。由于情绪分为基本情绪和复合情绪，若基于隐马尔可夫的情绪状态刺激转移模型仅能产生特定的基本情绪，还不够完善。如何使其能够产生复合的情绪，是一个需要解决的问题。

首先，引入辅助矩阵F_N×N，

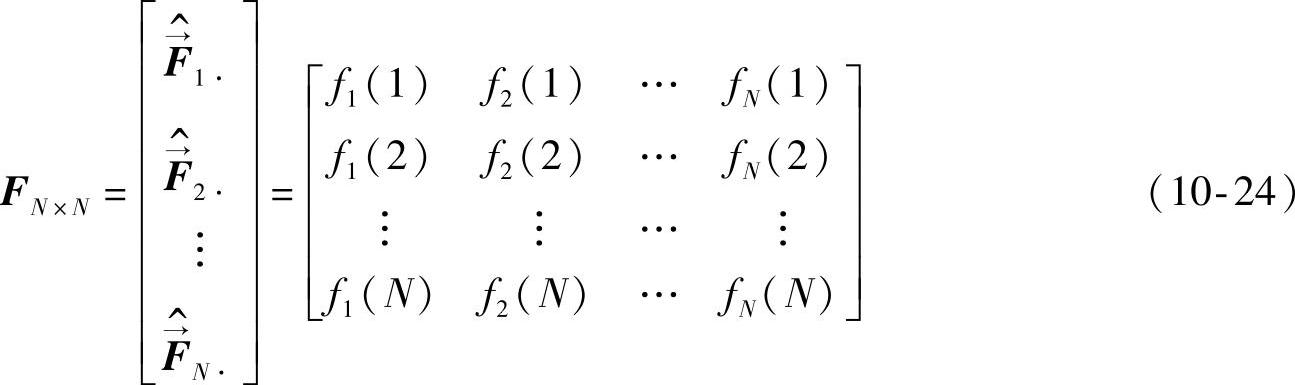
其中，行向量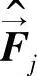·（1≤j≤N），对应第j种基本情绪类型的刺激。通过这个行向量的各个分量的值可确定刺激的类型。

令且ζ≤σ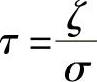，，（τ＞1），换元带入式（25），得到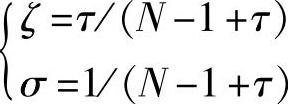{，τ＞1，进而得到辅助矩阵F。

为了使基于隐马尔科夫的情绪状态刺激转移模型产生复合情绪，需要减少上述理论假设条件。这种条件或约束的放宽，增加了情感模型的普适性。

复合情绪是由基本情绪的不同组合派生出来的，一种复合情绪类型的刺激可以引发若干种基本情绪，显然上述假设3是不合理的；同样，由复合情绪引发的几种基本情绪强度值也是可以同时同方向变化的，因此，假设4也不够合理。因此，要删除这两个假设。

其次，在剩余的四个假设条件下，根据辅助矩阵来计算HMM情绪状态刺激转移模型中的刺激矩阵。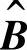

阵定义为

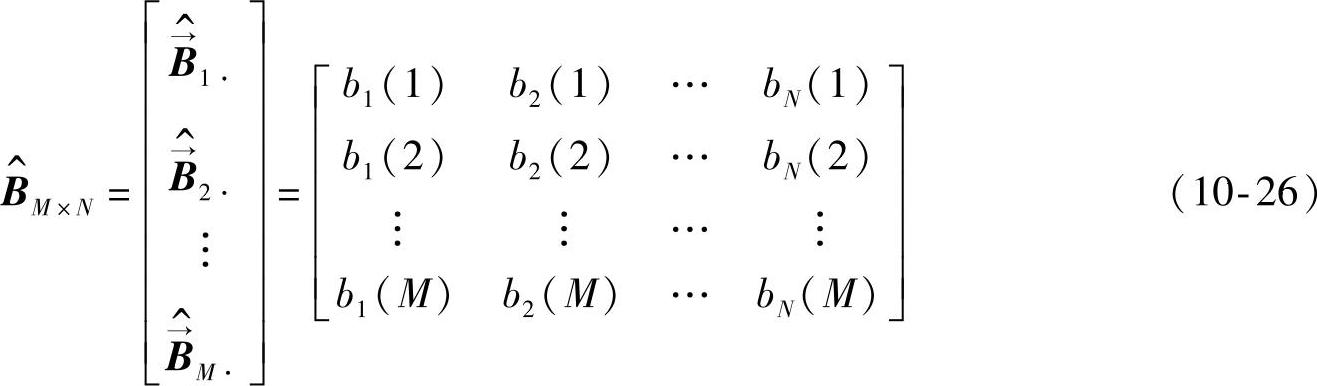
1）当刺激类型为基本情绪类型时，此时M=N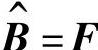，，这已在原有HMM情感模型中讨论；

2）当刺激类型为复合情绪类型时，例如复合情绪i是由基本情绪i，j，k组成的，则：

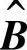阵第i行对应的行向量，即为复合情绪类型对应的刺激向量。

因为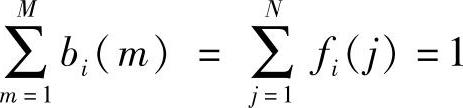，（1≤i≤N），所以阵依然满足HMM模型的使用要求，进而可以通过五元组λ=（N，M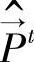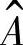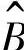，，，），计算情绪刺激转移过程中的情感状态值。

2.变阈值处理溢界问题

通过去除假设3和4，引入辅助矩阵F后，原有的HMM情感模型得到推广，能够产生由基本情绪组合成的复合情绪，增加了模型的适用环境。

但是在实际使用时，却存在情绪状态值的溢界问题。例如，某种复合情绪i是由基本情绪i，j组成的，当刺激事件持续刺激复合情绪时，相应基本情绪i，j的值都将增大，理论上他们都增大到0.5并会保持不变，实际上若此时出现小的扰动，使他们偏离0.5，根据HMM模型的计算，大于0.5的情绪将会被持续激发，逐渐增大到1.0并保持，而另一个小于0.5的情绪，将会被持续抑制，逐渐趋于0。

基于情绪状态刺激转移过程的HMM模型，情感强度值是通过前向-后向算法来计算的。

设前向变量为。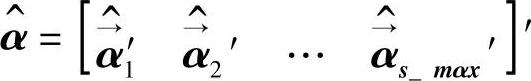

其中，

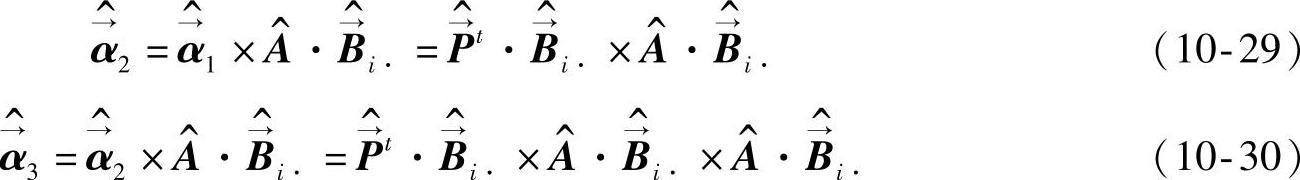
依此类推，

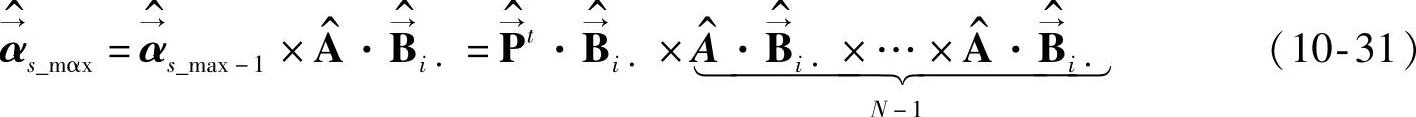
定义后向变量为β。

其中，

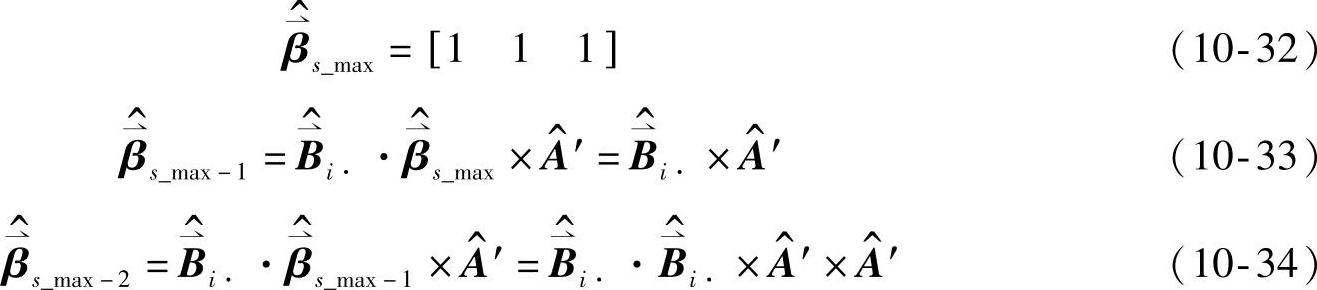
依此类推，(www.xing528.com)

计算。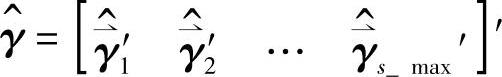

其中：

依此类推，

其中，s_max为最大刺激强度。

从式（10-38）看出，若情感状态向量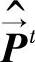中某两个基本情感状态值相同，在被激发后的下一时刻，这两个维度的值也应相同，因此，溢界问题应来自于其程序实现。

计算机在处理大量的浮点数运算时，由于计算的精度问题，看似相等的两个浮点数可能并不相等。通过分析程序，发现溢界问题来源于此。在计算时，应该相等的情绪状态维度会在浮点数的末位几个数字上出现微小差别，若刺激不断出现，上述基于HMM模型的情绪状态刺激转移过程会不断进行，这种微小差别就不断被放大，直至出现溢界。

这里通过引入一个可变的阈值ε来解决溢界问题。若某一种复合情绪类型的刺激激发的基本情绪越多，则ε越小。

ε=∝(1／num) （10-39）

其中，num是复合情绪类型刺激激发的基本情绪数量。

可变的ε在某一种复合情绪类型的刺激下，被赋为一个选定的值来控制“情绪状态近似度”。当N=3，溢界问题及其解决如图10-5所示。

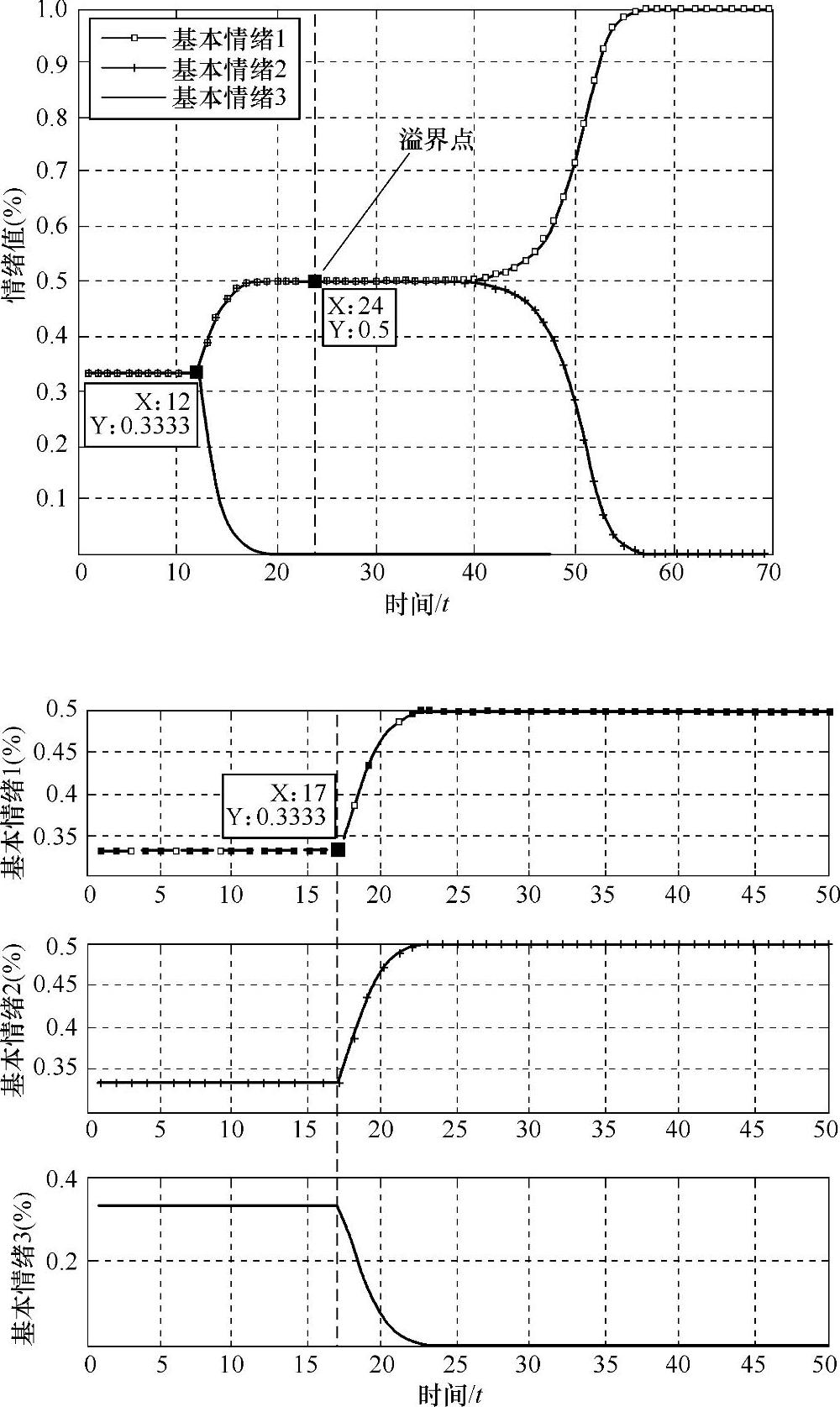
图10-5 溢界问题及其解决

图10-5左图中，在t=24时，出现溢界问题。由于计算的精度问题，情绪状态维度1与2的值在浮点数末位几个数字上出现了微小差别，进而在后续的计算中，这种差别被持续放大，使得基本情绪1与2的状态值出错。当加入了可变阈值ε后，溢界问题被解决，如图10-5右图所示，基本情绪1与2的状态值保持相等。

当N=6时，通过仿真试验发现，出现溢界问题的概率较小，这是由于每一个情绪状态维度值相对于N=3时都小很多，浮点数计算时末位较小的差别被舍去，情绪状态值都保持在合理的范围内，因而出现溢界问题较少。但也应加入可变阈值ε，保证算法的稳定。

3.仿真试验

设自发转移初始情绪状态向量、自发转移极限情感向量和刺激转移极限情感向量都为[1／N 1／N…1／N]，τ=1.06。基本情绪包括悲伤、愤怒、恐惧、厌恶、蔑视和愉悦六种，即N=6。下面将以嫉妒和敌意两种复合情绪分别出现后，情绪状态的变化过程来说明上述改进模型的有效性。

在t=7时刻出现嫉妒类型的刺激，一直保持到t=25时刻，撤销嫉妒类型的刺激，情绪的变化过程如图10-6所示。

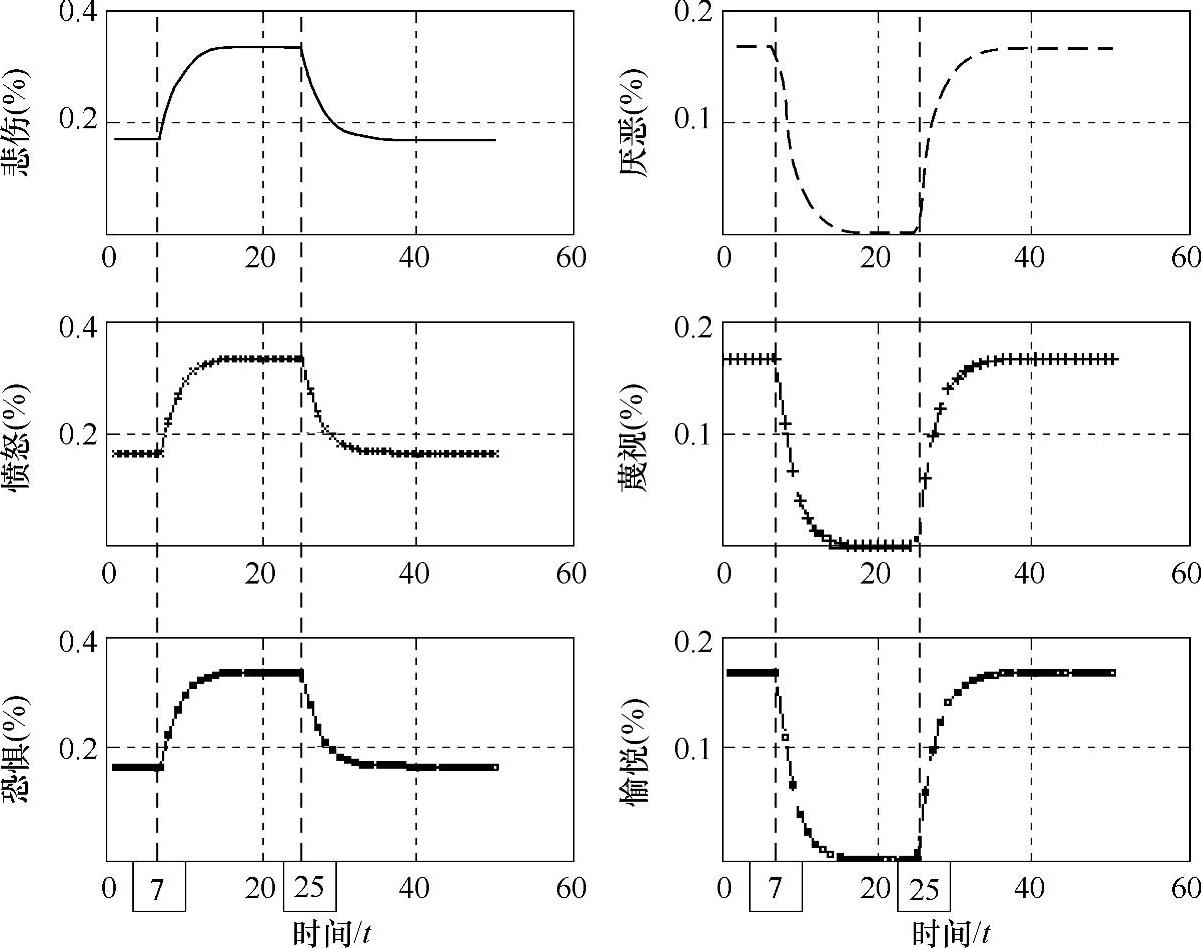
图10-6 嫉妒情绪的变化过程

由于嫉妒是愤怒混合着悲伤与恐惧，因此，在t=7时刻这三个维度的基本情绪得到激发，其他三个维度受到抑制；随后，嫉妒类型的复合情绪刺激并未消失，各基本情绪状态值继续增大或减小直至饱和；在t=25时刻撤销刺激，各维度的基本情绪逐渐恢复平静。

再次，设在t=7时刻出现敌意类型的刺激，一直保持到t=25时刻，撤销敌意类型的刺激，情绪的变化过程如图10-7所示。

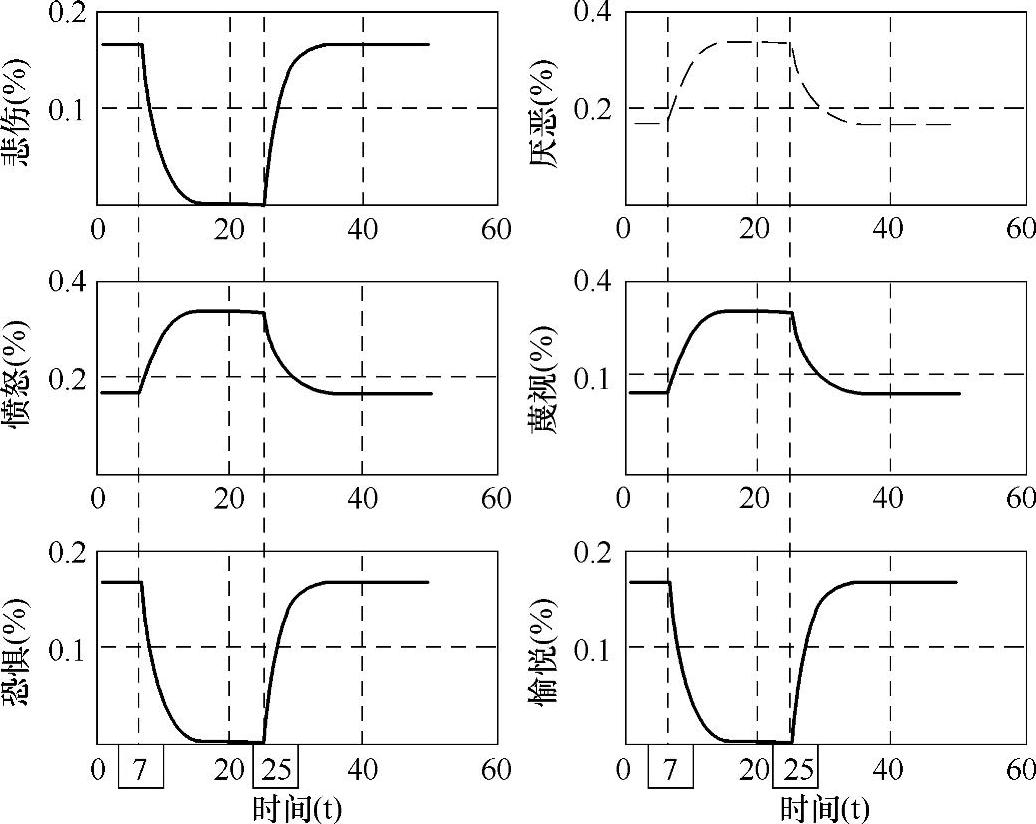
图10-7 敌意情绪的变化过程

由愤怒、厌恶和轻蔑组合起来的复合情绪可叫做敌意。同样，t=7时刻这三个维度的基本情绪得到激发，其他的三个维度受到抑制；随后，此复合情绪刺激并未消失，各基本情绪状态值继续增大或减小直至饱和；在t=25时刻撤销刺激，各维度的基本情绪逐渐恢复平静。

可以看出，通过对HMM情感模型的改进，能够更好的模拟复合情绪类型刺激出现、保持以及撤销后情绪的变化过程。

4.结论

在已有隐马尔科夫情感模型的基础上，通过减少假设条件并引入辅助矩阵，使原有模型产生复合情绪，增加了情感模型的普适性。同时，可变阈值为模型的计算机实现提供了基础，解决了情感状态计算时的溢界问题。

进一步研究的工作重点是改进基于HMM情感建模算法，使其为在人机交互过程中更好的实现拟人化计算机情感合成与输出做出理论贡献。