这种建模方法首先定义情感的两种状态(“心境”和“激情”)及其相对应的两个基本转移过程,提出情感状态的概率空间,并分别提出了基于马尔可夫链和HMM的情感转移变化模型,用来模拟情感的两个基本转移过程。通过情感能量、情感强度和情感熵等概念,描述情感特征与情感状态。通过计算仿真,验证所提出模型可以较为正确地模拟情绪状态的自发转移以及刺激转移过程,完整地描述情绪强度在外界刺激、当前心情状态和性格三方面综合影响下的变化规律,为情感计算和机器情绪自动生成理论研究提供了一种崭新的方法。建立的情感空间如图10-4所示。
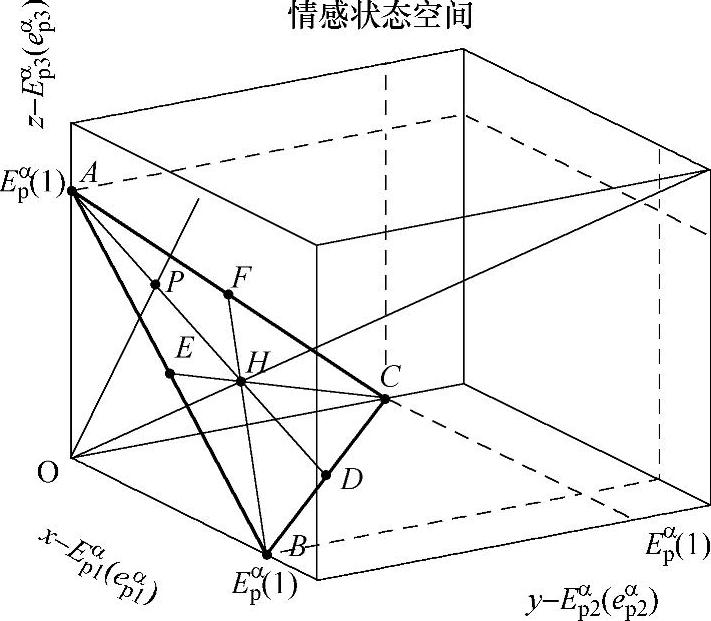
图10-4 基于概率空间的HMM情感模型
图10-4建立的情感空间坐标轴分别表示高兴、愤怒、恐惧三种情绪状态,用x、y、z分别表示。三维的绝对或相对情感能量分布方程可写成:
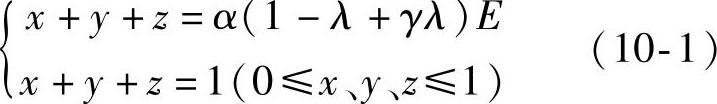
情绪状态自发转移过程的马尔可夫链模型和情绪状态刺激转移过程的HMM模型都建立在情感状态概率空间的基础上。其中,前者是用来模拟人们受到刺激一段时间后恢复平静的过程,后者是用来模拟人们受到刺激时情绪的变化。
1.情绪状态自发转移过程的马尔可夫链模型与算法
人类的情感是十分复杂的,要想使情感机器具有像人类一样丰富的情感及表现目前还十分困难。为简化问题,建立便于机器实现的情感度量与计算模型,制造具有基本人类情感或能近似模拟人类的基本情感,并和产生和谐、生动、有趣的人机交互效果的情感机器,我们需要做出一些基本的假设和限定。
如果用N表示基本情绪总数,i=1,2,…,N表示基本情绪序号,情绪状态可用下面的状态集合表示:
S={S1,S2,…,SN}={1,2,…,N},Si=i(i=1,2,…,N) (10-2)
假设1情感机器只具有人类的几种基本情绪状态。一般设定N=4,1=高兴、2=愤怒、3=恐惧、4=悲伤。
假设2即在外界刺激的作用下,情感机器的任意两种情绪状态之间可以互相转移。
假设3某种刺激确定性地引发某一种情绪,即刺激Vi只引发情绪i。刺激用Vi表示,刺激集合为
V={V1,V2,…,VM}={1,2,…,M},Vm=m(m=1,2,…,M) (10-3)
假设4各种基本情绪状态是互相排斥的。即刺激m=i应使情绪状态i的强度增加,而其他情绪状态j(j=i,j=1,2,…,N)的强度减少。
假设5情感状态的变化包括两个过程:心情状态自发转移和情绪状态刺激转移。
假设6心情状态自发转移的趋势是:总是向着平静心情状态转移。
情绪状态自发转移过程的数学模型:
在情感状态概率空间的基础上,情绪状态自发转移过程的基本方程为:

式中 P0=[p01,p02,…,p0N]——初始时刻情绪状态概率分布向量;
Pt=[pt1,p2t,…,pNt]——t时刻情绪状态概率分布向量;
A-t——t阶情绪状态自发转移矩阵;
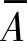 的极限概率分布为
的极限概率分布为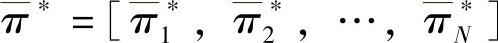 。由式
。由式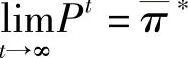 可知,
可知,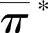 表示情绪状态自发转移过程最终处于稳定时的心情状态概率分布。
表示情绪状态自发转移过程最终处于稳定时的心情状态概率分布。
在式(10-4)中,P0和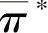 是事先给定的,只要确定了
是事先给定的,只要确定了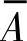 ,就可计算任意给定时刻t的情绪状态概率分布向量Pt,当t→∞时,有
,就可计算任意给定时刻t的情绪状态概率分布向量Pt,当t→∞时,有 。
。
状态转移矩阵的确定:
令: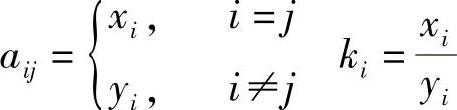
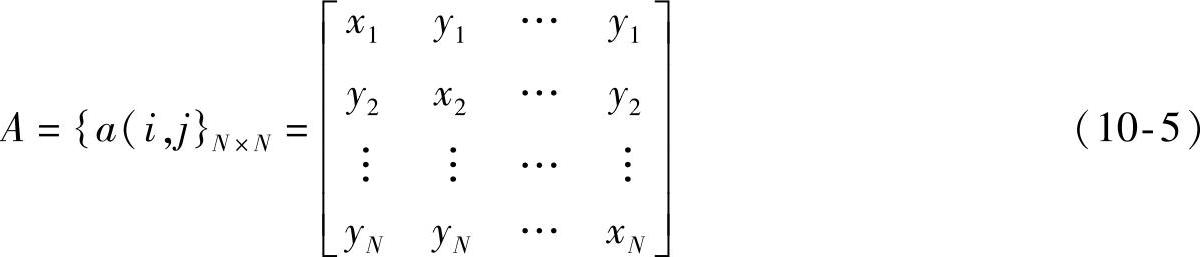

解上面二元一次方程并代入式(10-5)可得
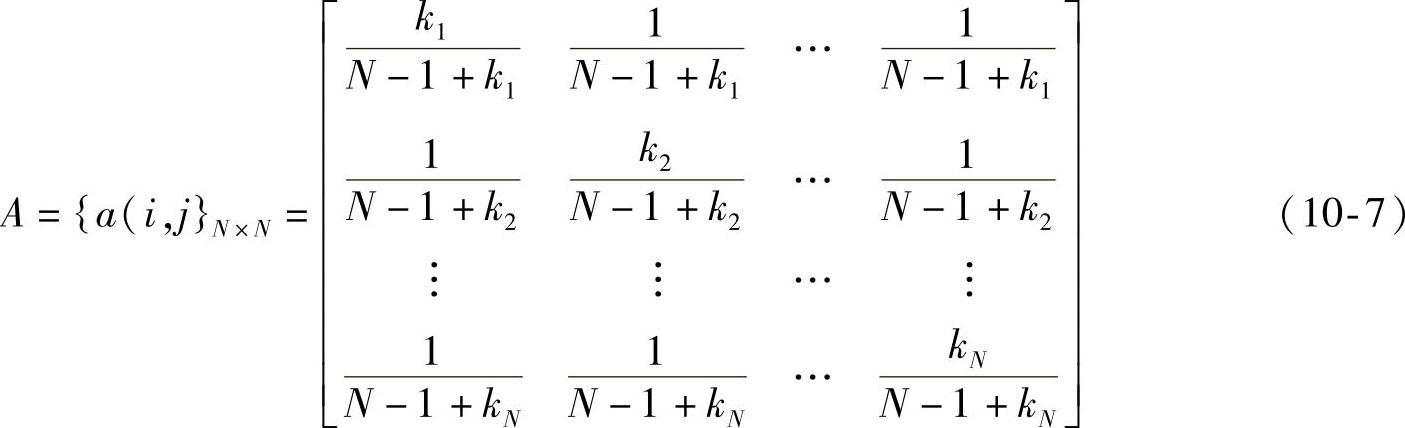
下面确定ki,其中i=1,2,…,N
由π∗A=π∗,π1∗+π2∗+…+πN∗=1得:

解得

将式(10-9)代入式(10-8)(N+1)式得
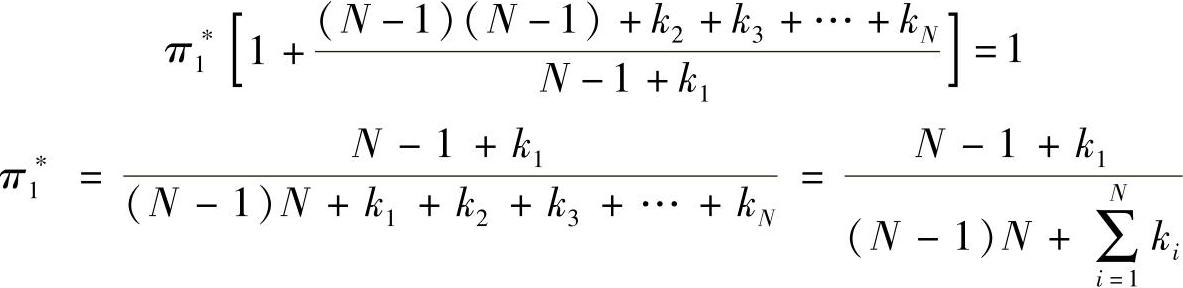 (https://www.xing528.com)
(https://www.xing528.com)
所以,
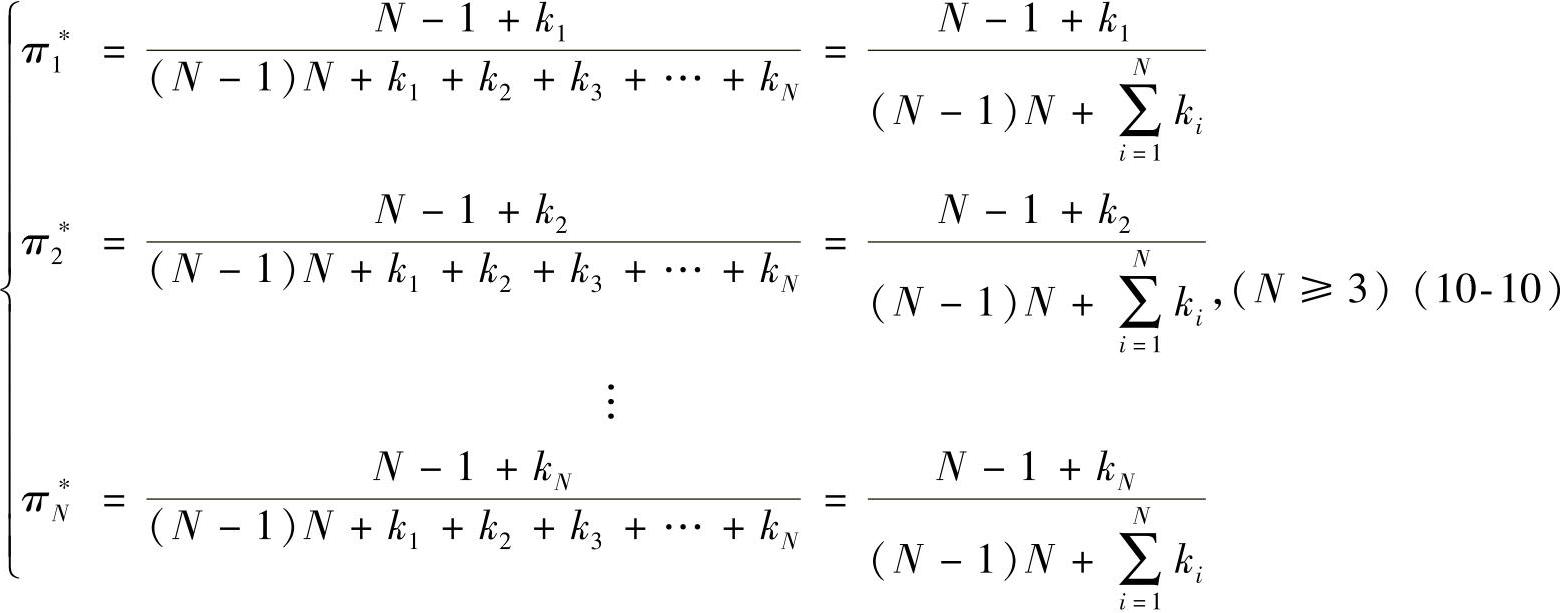
由式(10-10)得:
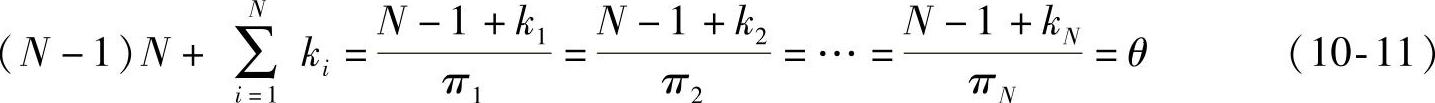
解得,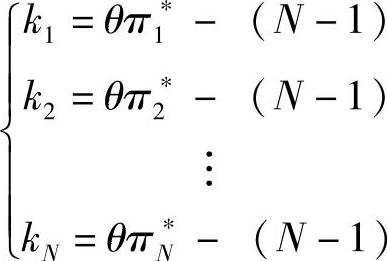
所以有,
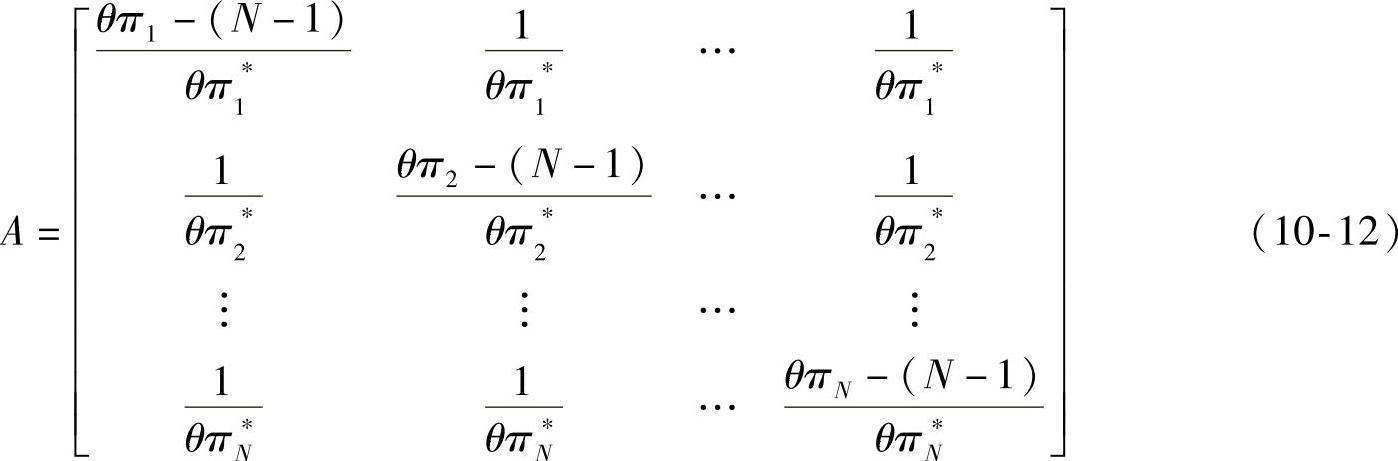
当N=4时,代入式(10-11)得:
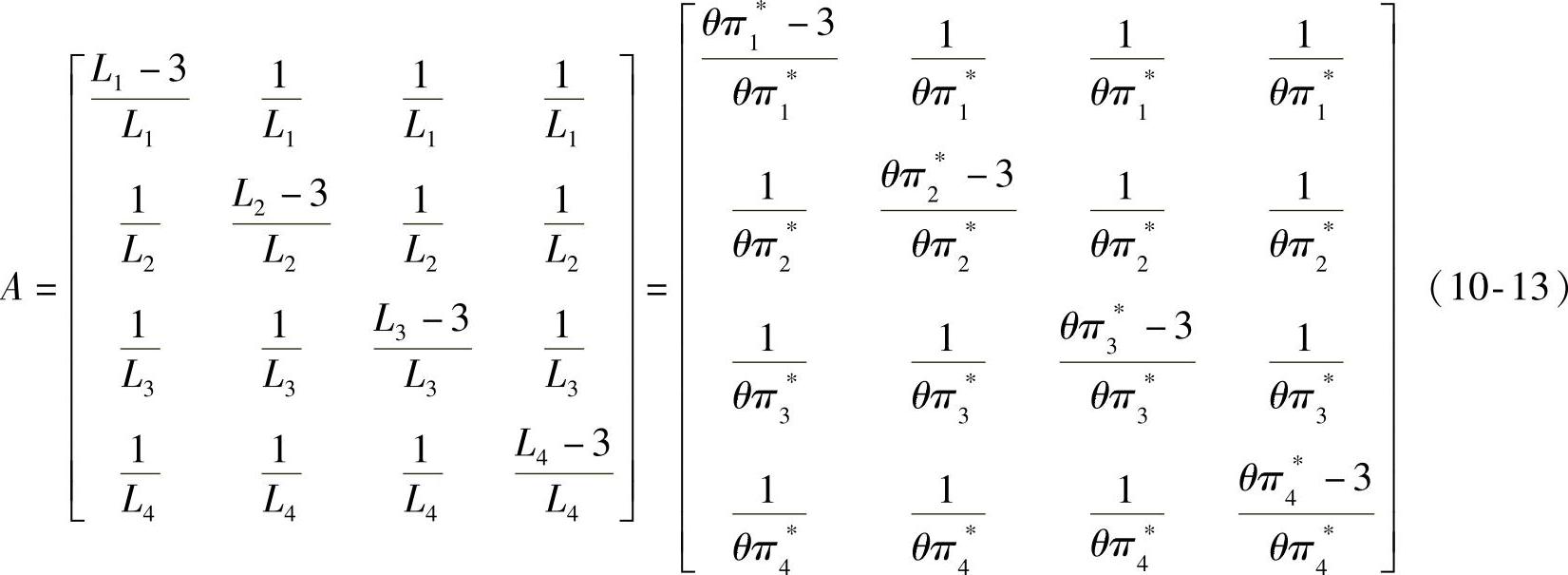
实际生活中,真实人的情绪在刺激事件影响后,情绪需要一个自发回落至平静的过程,因此情绪状态自发转移过程主要是为了模仿虚拟人在多个情绪刺激间隔时间内,情绪自动恢复平静的过程。
2.情绪状态刺激转移过程的HMM模型与算法
根据心理学理论,在有外界情感信息刺激的情况下,情感状态主要体现在情绪的变化上,而情绪的变化又受到多方面的影响,概括地说,主要由外界情感信息的刺激(类型、强度)、当前心情状态以及情感性格三个因素共同作用,可表示为λ=(N,M,π,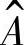 ,B)。其中,N表示基本情绪总数,M表示刺激类型,π是HMM模型中的初始概率分布,
,B)。其中,N表示基本情绪总数,M表示刺激类型,π是HMM模型中的初始概率分布,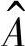 为情绪状态刺激转移矩阵,B表示刺激矩阵。
为情绪状态刺激转移矩阵,B表示刺激矩阵。
在情绪状态的刺激转移过程中,情感状态主要表现为情绪状态,情绪状态概率分布P=[p1,p2,…,pN]可用下面两个概率分布来描述。
初始心情状态概率分布:
初始心情状态概率分布,也就是HMM模型中的初始概率分布π,:π=[π1,π2,…,πN],它等于心情状态自发转移中的Pt=[pt1,p2t,…,ptN]。
当前情绪状态概率分布:
当前情绪状态概率分布P(T)=[p1(T),p2(T),…,pN(T)],表示与外界刺激的类型与强度T相对应的情绪状态。可通过前向变量计算和后向变量计算,得到状态概率分布pi(T)。
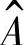 为情绪状态刺激转移矩阵,它的极限概率用
为情绪状态刺激转移矩阵,它的极限概率用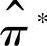 表示。具体可由式(10-14)来确定。
表示。具体可由式(10-14)来确定。

外界刺激可以用HMM模型中的观察值、观察值矩阵、观察值序列来描述。观察值集合也就是刺激集合为
V={V1,V2,…,VM}={1,2,…,M},Vm=m(m=1,2,…,M) (10-15)令观察值矩阵也就是刺激矩阵为:
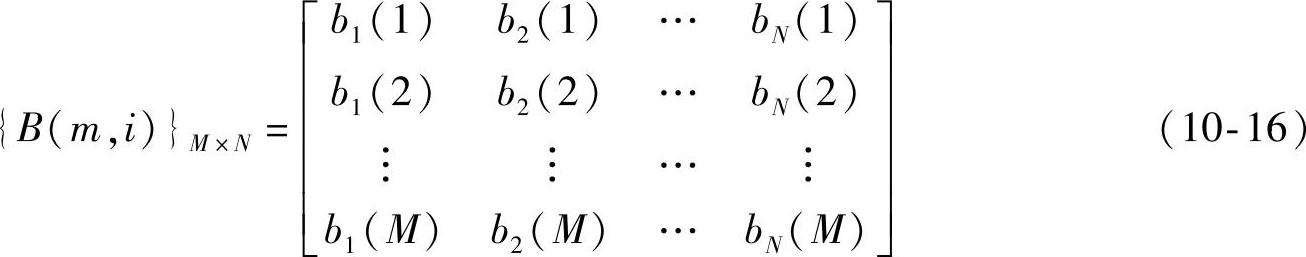
其中B(Vm)=[b1(m)b2(m)…bN(m)],(1≤m≤M)称为对应第m种情绪状态的刺激向量。刺激向量B(Vm)的各个分量的值可确定刺激的类型。且应满足:
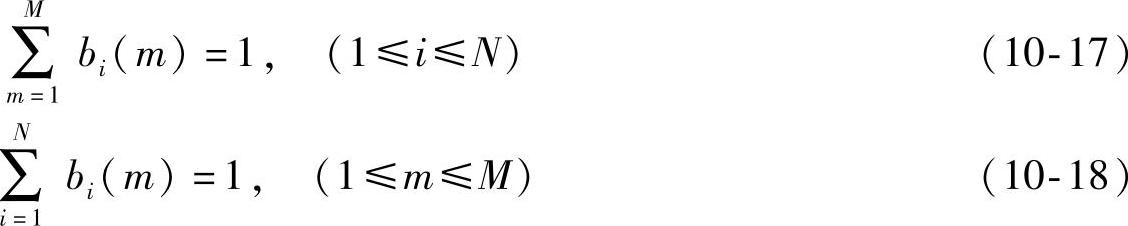
外界刺激矩阵的具体确定根据式(10-19):
令,
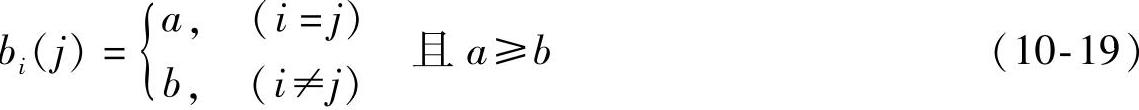
则刺激矩阵可写为

令,

r称为刺激影响因子。由式(10-18)得:
ɑ+(N-1)b=1 (10-22)
由式(10-21)和式(10-22)联合解得:

只要确定r,就完全可确定刺激矩阵{B(m,i)}M×N。
通过实用的情感信息获取手段,经过情感模型产生服务机器人自身的情感,再适当地表达出来,整个过程所涉及软硬件模块,构成了服务机器人的情感系统。嵌入此情感系统,可以为实现具有情感的个性化和谐人机交互提供有效途径。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




