实验结果与分析：摄像机标定及重投影误差分析

1.模拟实验

在试验中，设定了摄像机参数［f_u，f_ν，s，u₀，ν₀，k₁，k₂，p₁，p₂］分别为［1000，1000，0，320，240，0.1，－0.1，0.02，0.02］、图像分辨率为640×480。

为了验证本方法对噪声的敏感性，对各点加入噪声［Δx，Δy］，单位为像素，噪声水平为（0—1.0）。按照本章中的摄像机标定方法，在每个噪声等级下进行多次独立实验。求得每个噪声级别下的摄像机畸变参数，根据求解得到的结果重新计算该点在图像坐标系下的坐标，并与该点的准确值进行比较，得到重投影误差，如图5-4所示，可以看出，根据本方法求解出的值与真实值差别很小。

图5-4 重投影误差分析

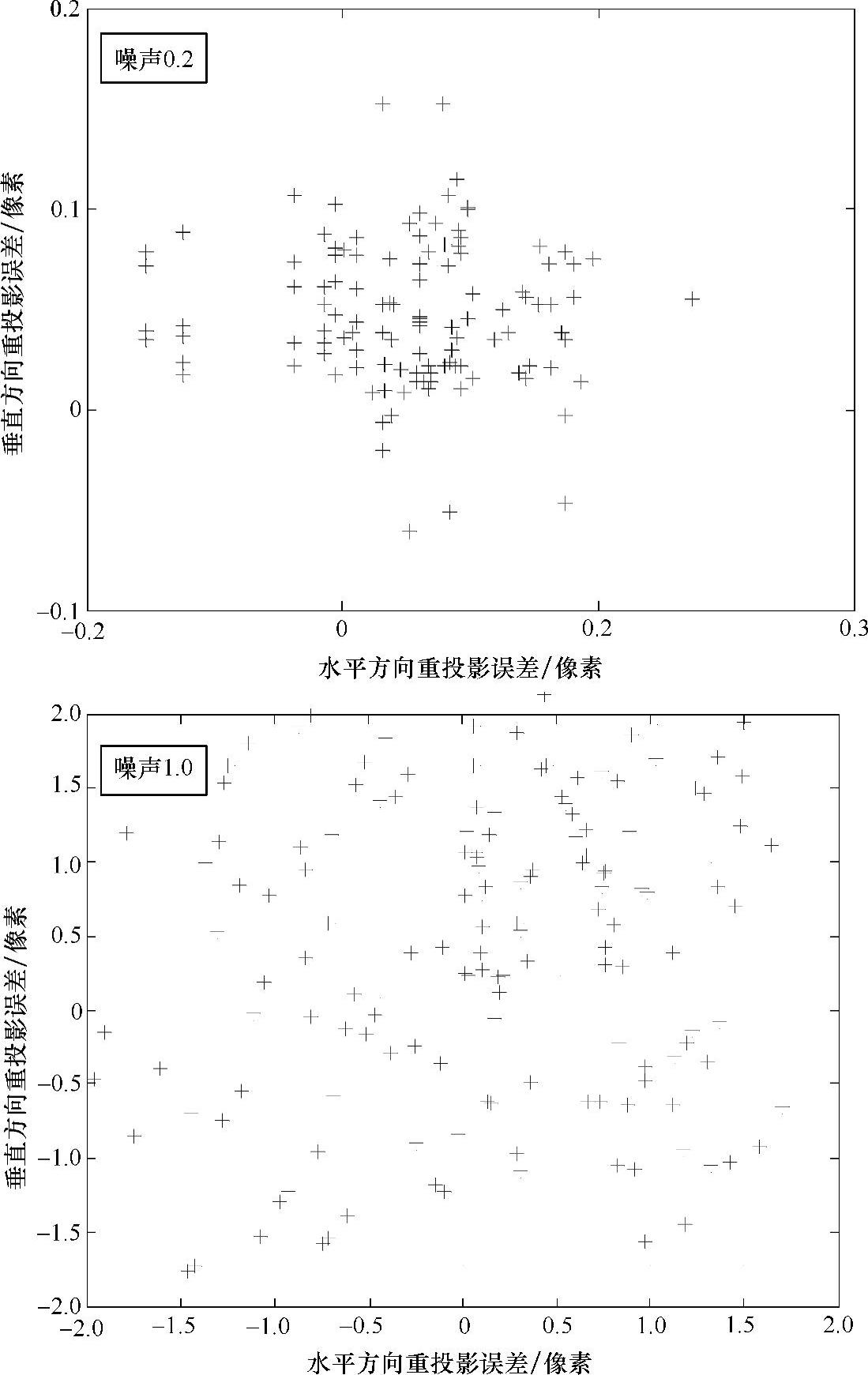
图5-4 重投影误差分析（续）

2.真实实验

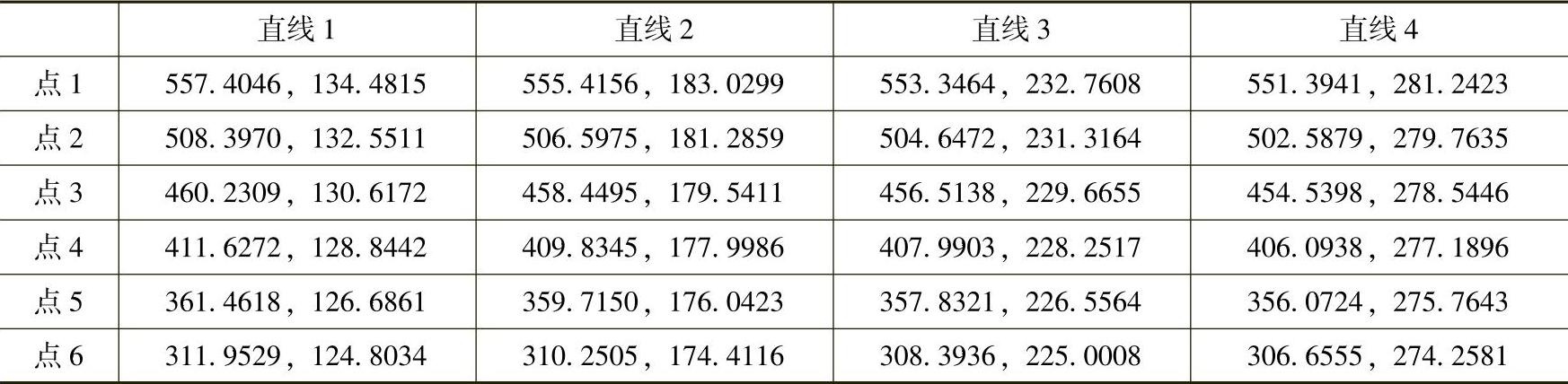
从拍摄的20幅图像中选择一幅，其模板如图5-5a所示，棋盘格角点的图像坐标见表5-1。

表5-1 图像中部分直线上点的图像坐标

(www.xing528.com)

图5-5 拍摄的标定模板

a）原始图像 b）去畸变后图像

根据这些点，按照本章中的去畸变方法，得到畸变参数见表5-2。

表5-2 畸变参数

经过摄像机畸变校正得到的摄像机内参数矩阵为

针对图5-1中的模板参数得到以下矩阵

本书提出此种基于直线的摄像机镜头去畸变方法，针对标定参数较多的问题，先进行畸变校正，再标定摄像机的内外参数。在畸变校正的过程中，使用线性迭代方法，有效避免了非线性算法的初值选择困难、易于收敛于局部最小值等问题，且精度较高。