摄像机的成像模型

1.理想的摄像机成像模型

理想的无透视畸变成像模型是小孔成像模型，它是最简单的摄像机成像模型。设空间一点P（X，Y，Z），其在图像上的透射投影为p（x，y），设f为摄像机焦距，根据透射投影的关系有

用矩阵表示为

根据世界坐标系与其在图像上的投影关系可得

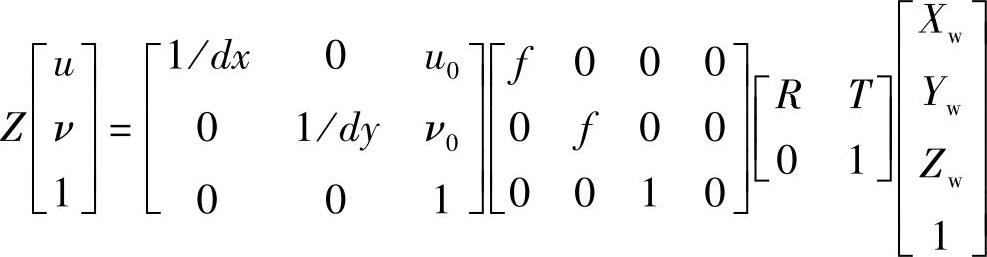
即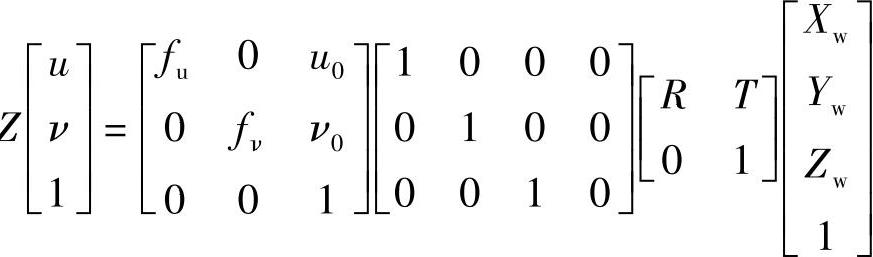

考虑到读取图像过程中可能会导致CCD敏感像元数和缓存中像素数不相等的情况，定义一个比例因子s作为补偿。上式最终可表示为

我们称矩阵为摄像机标定内参数矩阵，其所有的参数只和摄像机本身有关。而R、T为摄像机外参数，由摄像机相对于世界坐标系的方位决定。

2.摄像机畸变模型

在实际应用中，由于摄像机镜头的畸变和装配误差等影响，实际得到的图像存在畸变。因此，在精度要求高的场合，需要考虑图像的畸变。图像畸变通常包括径向畸变、切向畸变和薄棱镜畸变，图5-2所示为理想无畸变图像点位置和有畸变图像点位置之间的关系。

图5-2 径向畸变与切向畸变图像点位置之间的关系

畸变模型的一般表达式为

其中，［x，y］^T表示理想情况下的点坐标，［x_d，y_d］^T表示存在畸变的点坐标。Δ_r为径向畸变，Δ_d为偏心畸变中的切向畸变，Δ _t为薄棱镜畸变。一般来说，薄棱镜畸变影响较小，不予考虑。径向畸变和切向畸变已足够描述非线性畸变。

Δx_r=x_d（k₁r²_d＋k₂r²_d）Δy_r=y_d（k₁r²_d＋k₂r²_d）

Δx_d=p₁（r²_d＋2x²_d）＋2p₂x_dy_d Δy_d=p₂（r²_d＋2y²_d）＋2p₁x_dy_d

令q=［k₁，k₂，p₁，p₂］^T，q为畸变参数向量，则上式可写为(www.xing528.com)

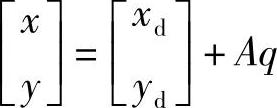
其中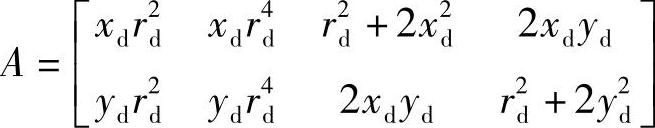

图5-3 空间直线投影到像平面

3.摄像机模型畸变参数

根据摄像机畸变的原理，我们观察图像发现越远离图像中心图像畸变越严重，一条直线往往变形成类似圆弧的曲线，而由摄影几何可知，空间直线在像平面的投影仍是直线，如图5-3所示。

设空间直线投影到像平面的直线方程为xsinθ－ycosθ＋ρ=0，其中，θ是直线与x轴夹角，ρ为直线到原点的距离。

设一组空间直线投影到像平面，令I_i（i=1，2，…n）为含有投影直线的图像，I_i上包含直线l_ij（j=1，2，…N），直线l_ij上的点为P_ijk（x_ijk，y_ijk）（k=1，2，…N′），直线l_ij与x轴夹角为θ_ij，到原点距离ρ_ij。直线l_ij满足x_ijk sinθ_ij－y_ijk cosθ_ij＋ρ_ij=0，将代入，有

（x_{ijk d}＋^Δx_{ijk r}＋Δxijk d）sinθ_ij－（y_ijk d^＋Δy_ijk r^＋Δyijk d）cosθ_ij＋ρij=0，令

这样，求解摄像机畸变参数问题被转换为一个求解无约束最小值的问题

通常求解这类问题使用非线性求解算法，如共轭梯度法、L-M法等。非线性算法虽然具有收敛速度快、精度高等特点，但也存在着初始值的选择困难等问题，因此选用了线性的迭代算法求解。上式也可以写为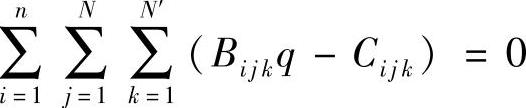，其中

我们按以下过程进行迭代求解：

1）直线l_ij的初始特征点坐标［x_ijk（0），y_ijk（0）］，初始化迭代次数m=0；

2）使用最小二乘拟合直线l_ij的参数θ_ij（n）、ρ_ij（n）；

3）求解方程组3-11，得q（n）；

4）计算ξ（n）=q（n）－q（n－1），如果ξ（n）＜ξ，转到6；

5）n=n＋1，按式3-5计算（x_ijk（n），y_ijk（n）），转到2；

6）计算结束。