手臂避障仿真优化实践

双臂间协调避障是机器人研究的一个热点，本节基于前几节双臂避障模型及理论的基础上，以五自由度情感机器人的双臂为例，使机器人双臂进行交叉运动。本文规定双臂的右臂为主臂，左臂为从臂，主臂具有较高的运动优先权。给定机器人的左右臂各自起点、目标点，规划出机器人双臂避障运动轨迹。避障算法首先判断主臂和从臂在各自进行作业时是否发生碰撞，若发生碰撞，则使具有优先运动规划权的主臂先完成规划动作，然后从臂把主臂作为障碍物处理，并规划出一条无碰撞的轨迹。对机器人双臂未采用避障算法和采用避障算法分别进行仿真，通过仿真比较验证避障算法的可行性。

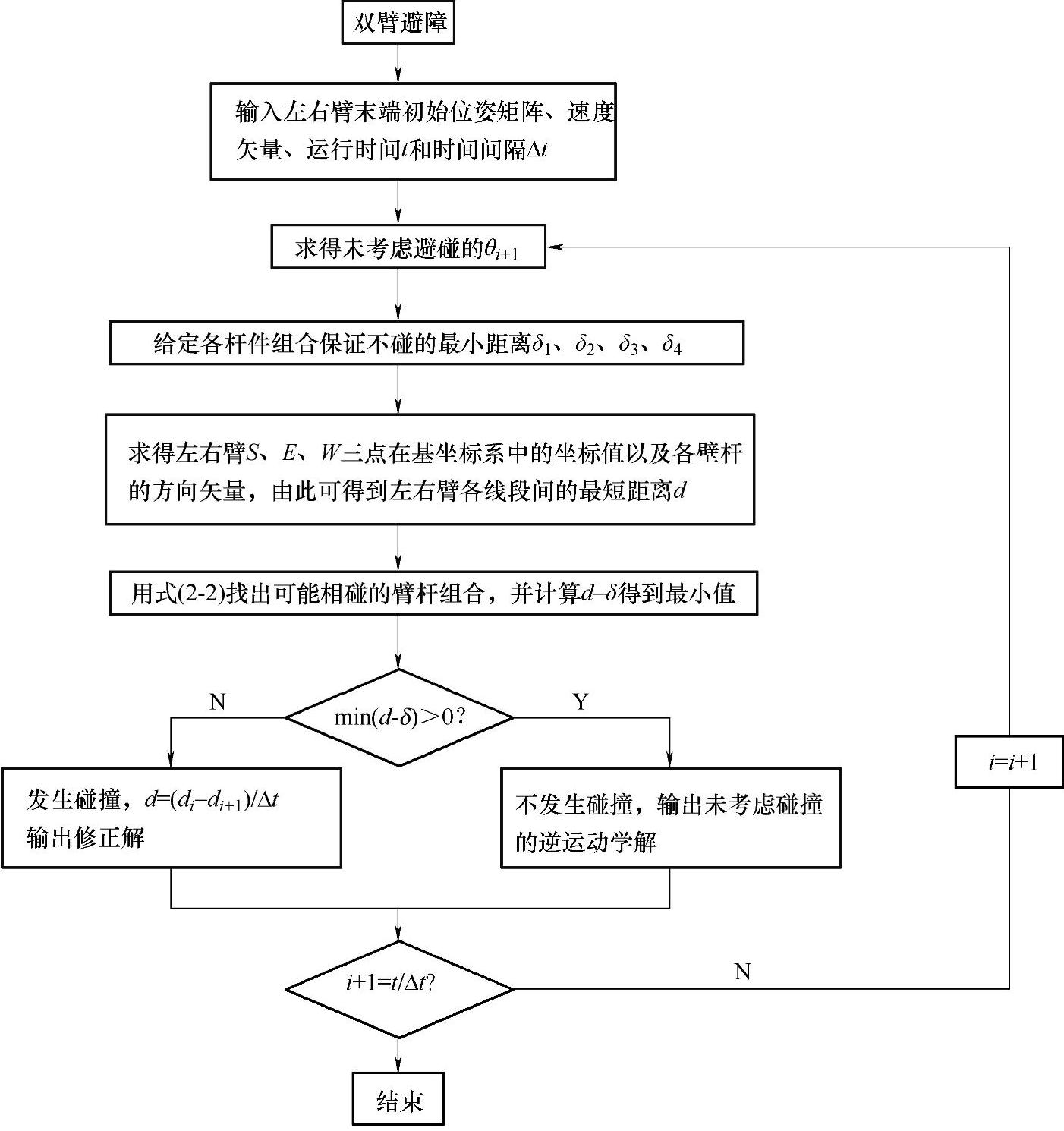
图2-30 双臂避障算法的流程图

在手臂运动学研究的基础上，以五自由度手臂（双臂共十个自由度）为例进行仿真。以图2-28所示坐标系及图2-31所示起始点及目标点进行计算，右臂起始点A₁（－376，0，－125）到目标点A₂（－270，100，25）；左臂起始点B₂（－376，0，125）到目标点B₂（－270，100，－25）。由此可得A₁、A₂、B₁、B₂的位姿矩阵为

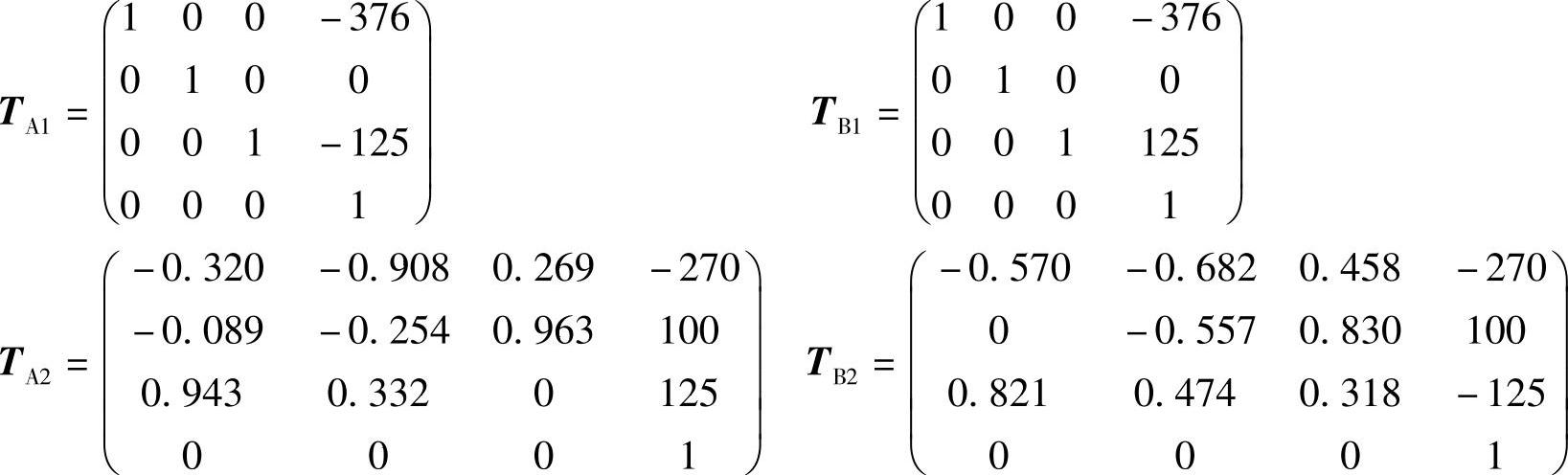
右臂是主臂，具有较高运动优先权，故而从A₁运动到A₂不需采用避障算法，而左臂是从臂，由B₁运动到B₂，关节角速度不大于±90°／s，仿真时间为5s，采样时间为0.5s。

图2-31 轨迹规划的起始点及目标点

a）起始点 b）目标点

计算出大臂在公共坐标系中的方向数为

右大臂（－0.963，0，0.269）；左大臂（－0.963，0，0.269）；

右小臂（－0.478，－0.496，0.134）；左小臂（－0.478，0.867，0.134）。

按照式（2-1）进行计算可知，大臂杆不会相碰而小臂杆已经碰撞，现在已找出相碰杆组合，然后进行输出修正。

根据避障算法的流程将修正解返回计算，由于右臂是主臂，只计算左小臂的方向数为（－0.963，0，0.269），双小臂不碰的最小距离δ=0.3m，经修正计算后的小臂杆直接最短距离满足d=0.455＞δ，因此不发生碰撞，输出碰撞的运动学逆解。将所求解应用Origin7软件仿真可以得出关节角度的变化曲线。

Origin7具有两大类功能：数据分析和绘图。数据分析包括数据的排序、调整、计算、统计、频谱变换、曲线拟合等各种完善的数学分析功能。准备好数据后，进行数据分析时，只需选择所要分析的数据，然后再选择响应的菜单命令就可以完成其数学分析过程。Origin的绘图是基于模板的，Origin本身提供了几十种二维或三维绘图模板而且允许用户自己定制模板。绘图时，只要选择所需要的模板便可以。用户可以自定义数学函数、图形样式和绘图模板；可以和各种数据库软件、办公软件、图像处理软件等方便地连接；可以运用C等高级语言编写数据分析程序，还可以使用内置的Lab Talk语言编程等。

通过Origin7绘图是将复杂的计算数据以图线的绘图形式展现出来，有利于我们对避障算法进行分析与研究。我们先将运动学逆解数据导入该软件，然后通过软件输出我们所需要的输入、输出图线。Origin7软件界面如图2-32所示。

为了求得在关节空间中形成的轨迹，我们首先用运动学反解将路径点转换成关节矢量角度值，然后对每个关节拟合一个光滑函数，在满足所要求的约束条件下，可以选取不同类型的关节插值函数，以生成不同的轨迹。常用的插补算法有线性插补、分段插补及多项式插补等。(www.xing528.com)

线性插补会使线性插值关节在起点和终点的速度和加速度不连续，运动不平稳，且加速度无穷大，显然在两端会造成刚性冲击。抛物线分段插补可以保证起点和终点的速度平稳过渡，从而使整个轨迹上的位置和速度连续，但又出现了起点和终点加速度不连续的情况。因此，必须建立一个五次多项式（2-3）进行插值即可以实现系统的平稳运动。

θ_t=ɑ₀＋ɑ₁t＋ɑ₂t²＋ɑ₃t³＋ɑ₄t⁴＋ɑ₅t⁵ （2-3）

如果未采用避障算法，则右臂和左臂都将按照起始点到目标点的运动轨迹进行，那么左、右臂同时到达目标点位置后就会产生左、右臂小臂杆相碰撞的情况，左、右臂末端位置姿态构型如图2-33a所示。计算出左臂的关节角度变化曲线如图2-34a所示。

如果采用避障算法时，右臂是主臂，右臂从起始点运动到目标点仍然按照预定的运动轨迹进行，而左小臂是从臂，则会绕开右小臂到达目标点位置，左、右臂末端位置姿态构型如2-33b所示。计算出的左臂的关节角度变化曲线如2-34b所示，经比较可知避障后的左臂关节1、3、4会与未避障时的关节角度有明显改变。

图2-32 Origin7软件界面

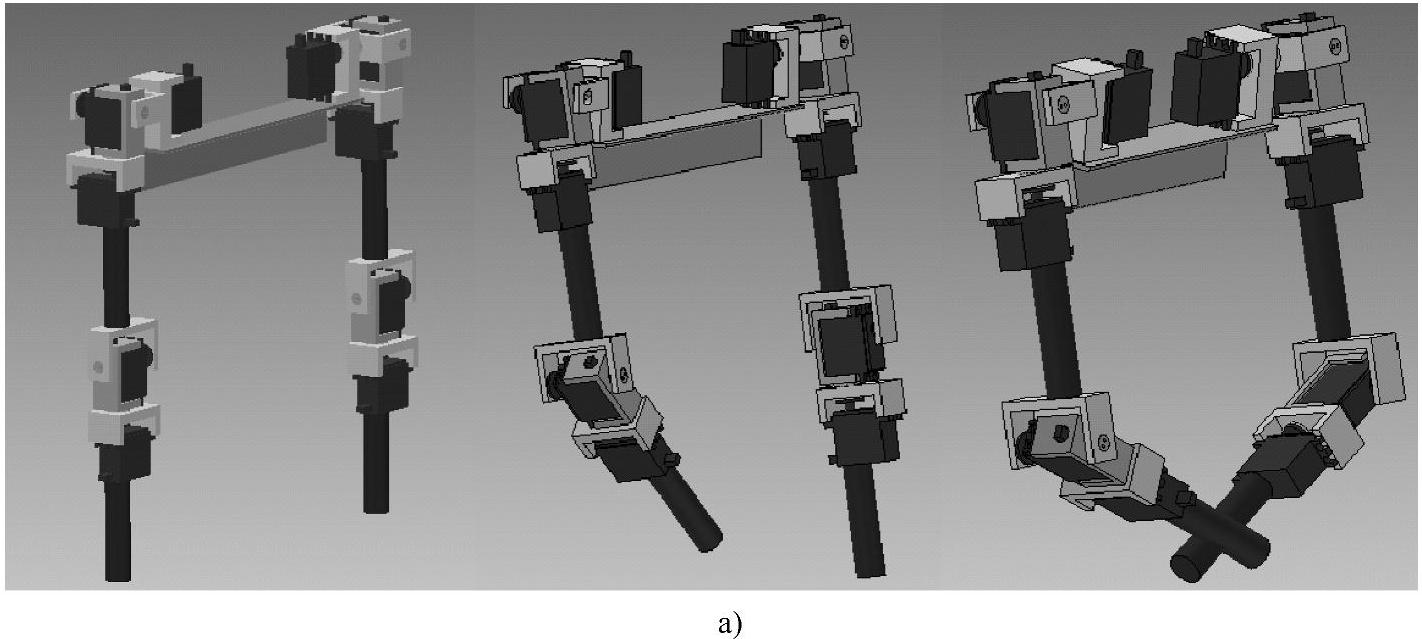
图2-33 末端姿态构型仿真结果

a）未采用避障算法得到的仿真结果

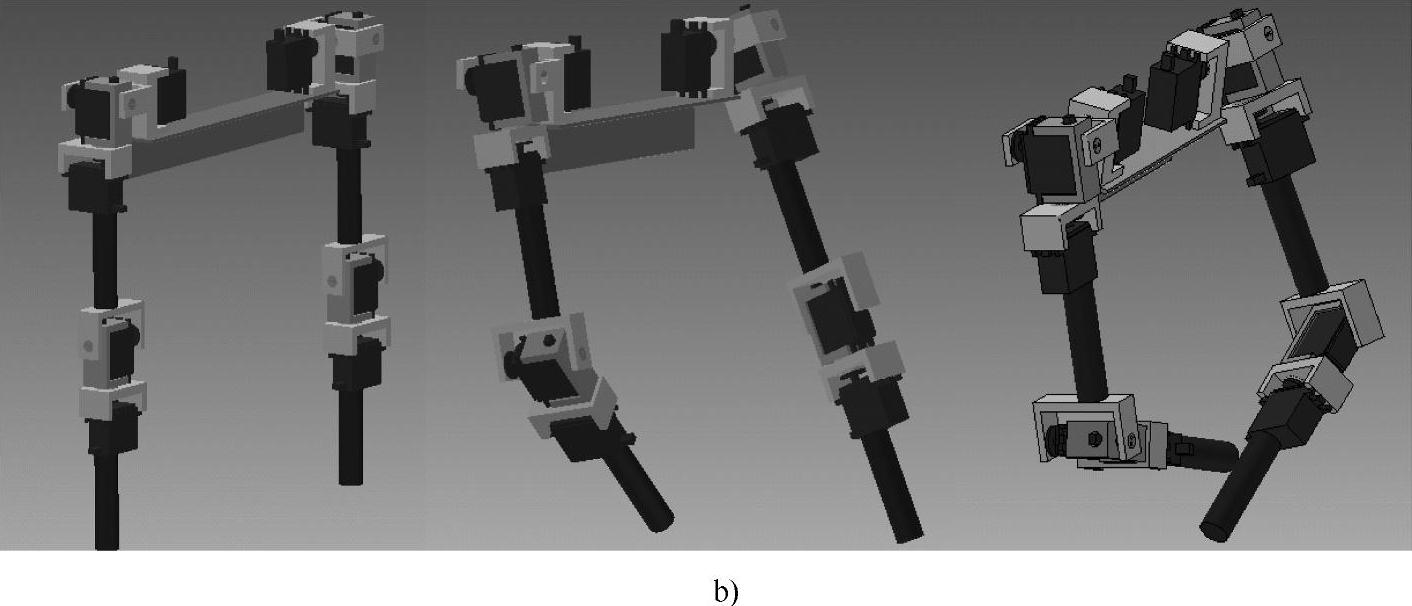
图2-33 末端姿态构型仿真结果（续）

b）采用避障算法得到的仿真结果

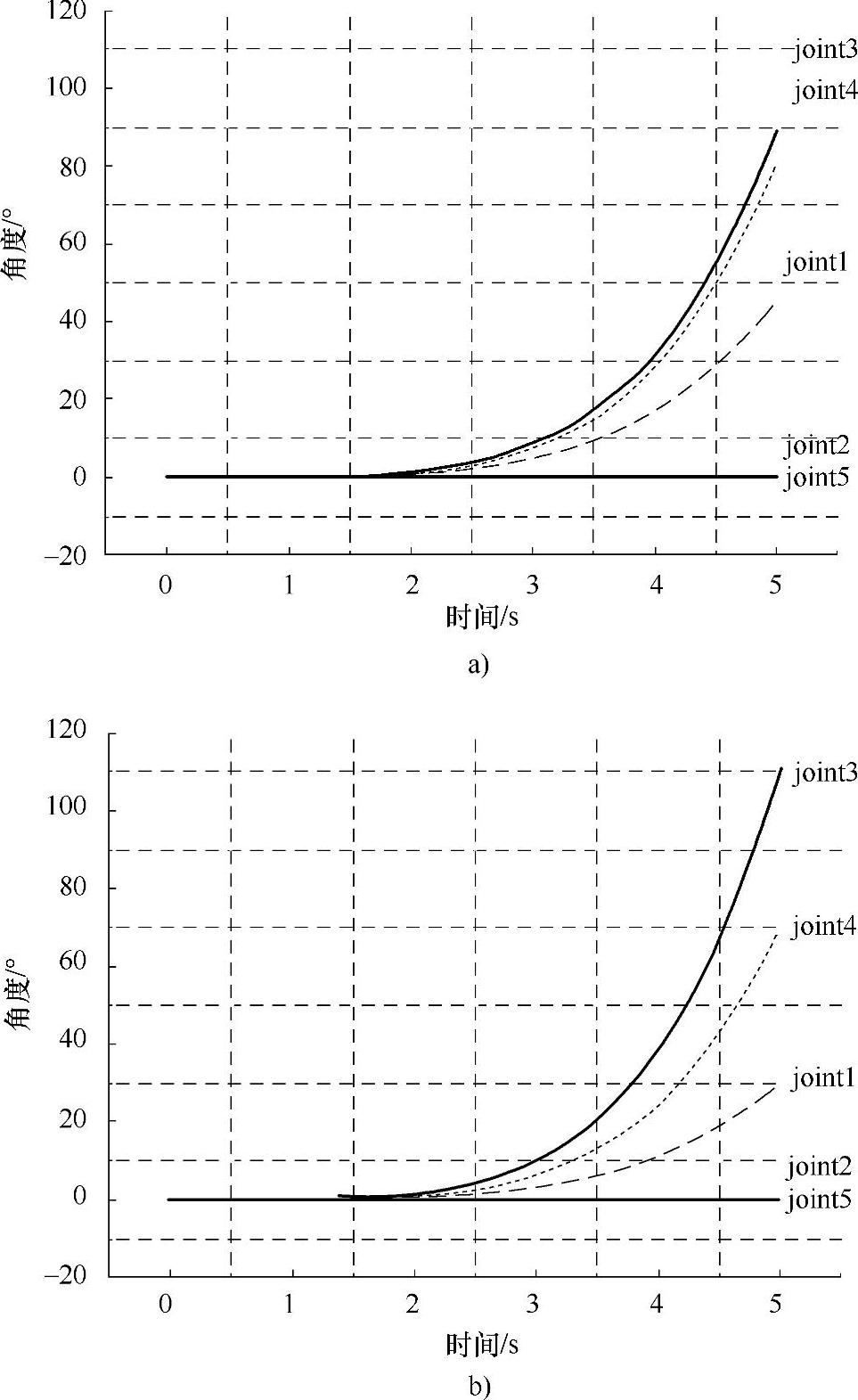
图2-34 左臂的关节角度变化曲线

a）未采用避障算法得到的关节角度变化曲线 b）采用避障算法得到的关节角度变化曲线