机器人眼睑正逆运动学与轨迹规划

机器人头部运动学仿真涉及正运动学、逆运动学、工作空间、轨迹规划等问题。本文通过分析实物，发现表情头的头部各部位的运动其实是带有闭链的串联连杆的运动，其中闭链的四杆机构是驱动器，可以驱动其他连杆运动，由于我们是在关节空间中分析问题，而不是在驱动空间，这样我们就不必考虑四杆机构，直接把它简化成被驱动的连杆，使问题得到简化。通过Pro／E三维造型，得到各关节的具体尺寸，为我们分析问题提供了方便。

机器人眼球的正运动学分析，建立如下坐标系：共设五个坐标系——S₁，S₂，S₃，S₄和S₅，如图2-16所示，这里我们采用的是后置坐标系。其中坐标系的Z与关节轴重合，坐标系的原点位于两关节轴公垂线与关节轴的交点，X轴沿公垂线由前一关节指向后一关节。机器人眼球运动各杆件参数见表2-5。

两杆间的位姿矩阵，根据参数表和D-H公式可得

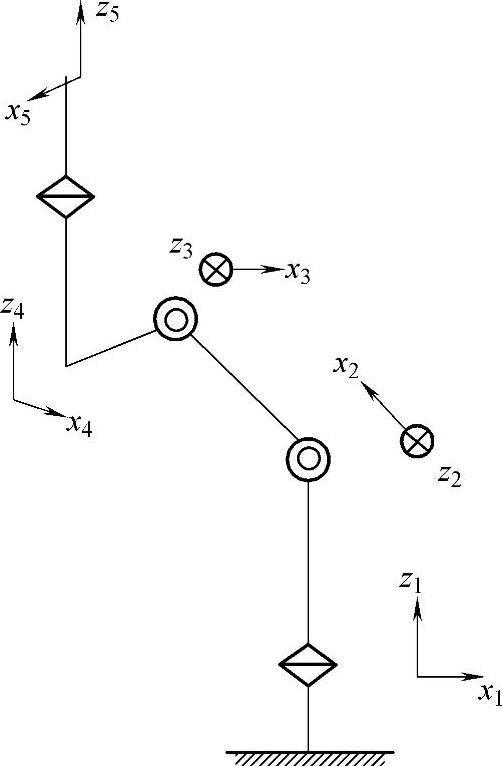
图2-16 机器人眼球坐标系

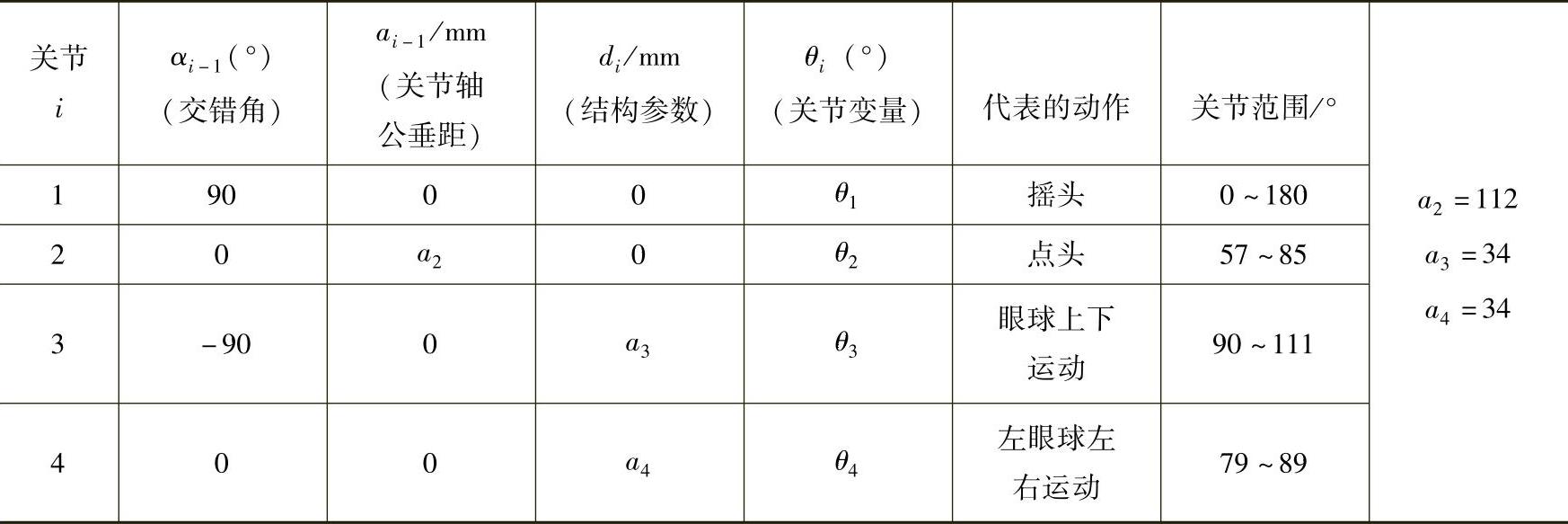
表2-5 机器人眼球运动各杆件参数

将各个连杆矩阵连乘得到₅¹T

式中

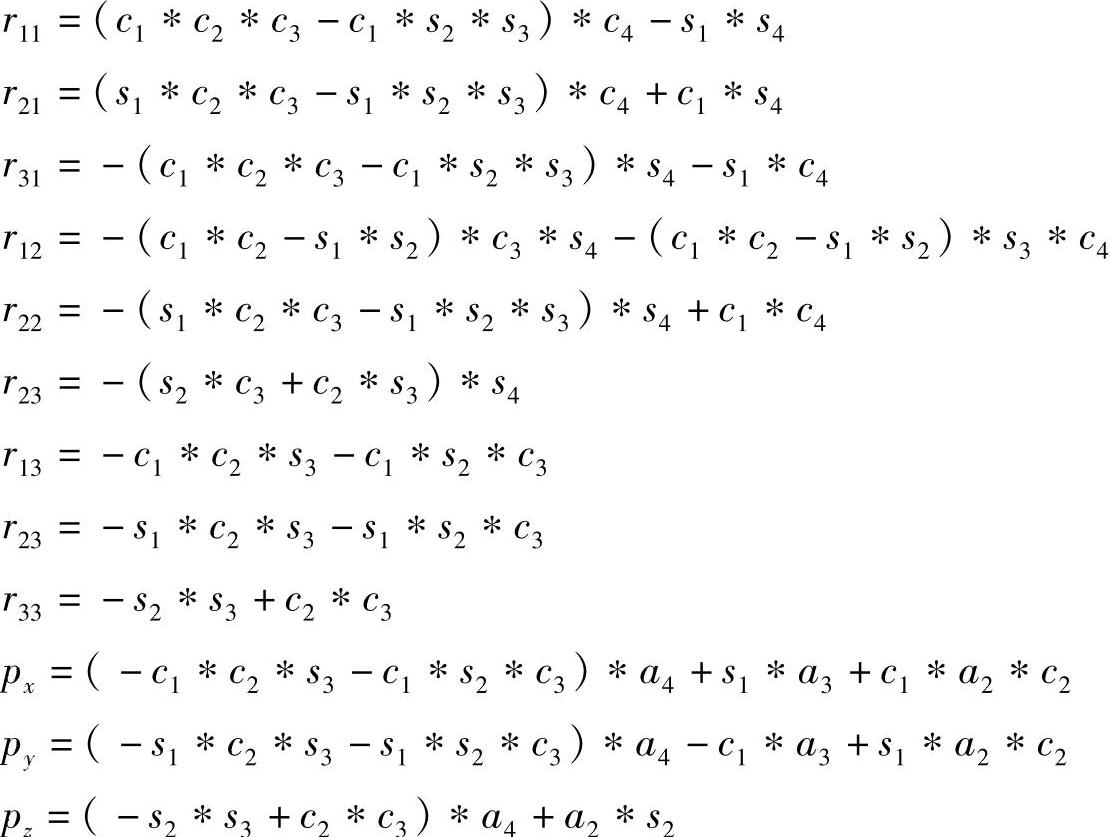
其中c_i=cosθ_i（i=1，2，3，4）；s_i=sinθ_i（i=1，2，3，4）

于是可得眼球作为末端执行器的姿态和位置分别是

机器人眼球的运动仿真，通过matlab中的robot tools工具箱，建立从机器人脖子到眼球的运动模型，在控制面板（见图2-17）的控制框内输入4个关节角的值，便可以计算出眼球相对于基础坐标系的空间位置，如图2-18所示的三维立体图（图示为起始状态），这样，就可以驱动机器人头部运动，其效果如同实际控制机器人一样。

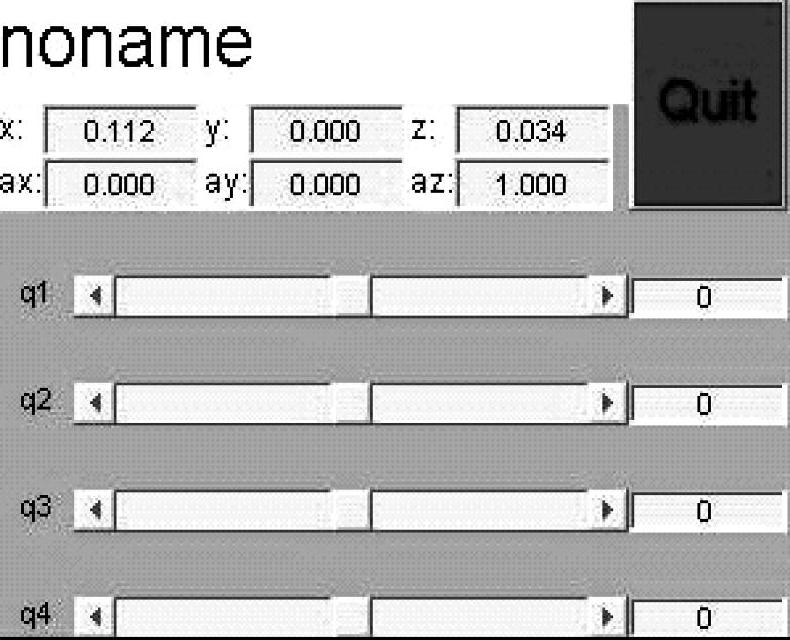
图2-17 控制面板

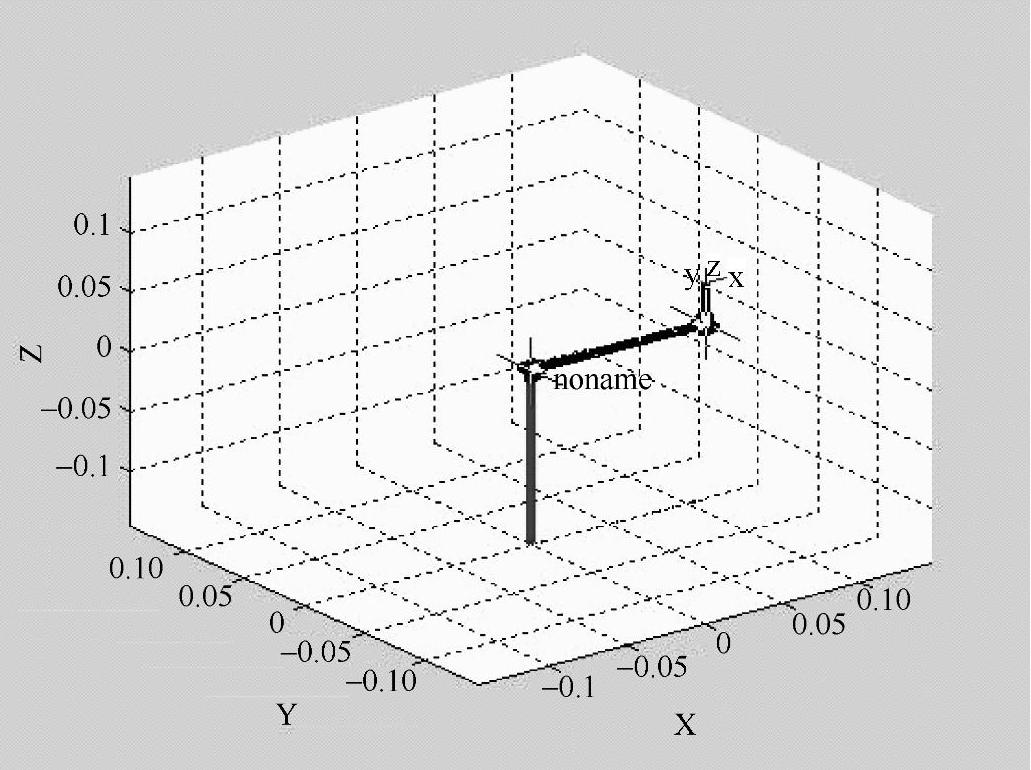
图2-18 三维立体图

1.正运动仿真实例

假定机器人眼球初始关节量q=［0000］，此时眼球位于空间N₁=（0.112，0.000，0.034）的位置，当运动到空间N_e=（0.115，－0.005，0.075）时关节变量就会变化至q_e=［0.251320.37698－0.565470.18849］，通过matlab仿真，可以生成机器人从起点运动到终点的关节坐标轨迹。例如第一个点为

T（：，：，1）=

1.0000 0 0 0.1120

0 1.0000 0 0

0 0 1.0000 0.0340

0 0 0 1.0000

最后一点为

T（：，：，36）=

0.8880 －0.4226 0.1815 0.1070

0.4214 0.9057 0.0466 0.0275

－0.1841 0.0351 0.9823 0.0746

0 0 0 1.0000

运动学验证，对终止位置关节量进行赋值：(www.xing528.com)

θ₁=0.25132，θ₂=0.37698，θ₃=－0.56547，θ₄=0.18849

代入公式姿态矩阵和位置矩阵可得

和上面公式中的最后一点的位姿矩阵结果完全符合，可见正运动学模型完全正确。

仿真结果分析：通过仿真，可以看出机器人头部各关节在运动过程中情况正常，运动平稳，连杆之间没有错位冲突的情况，验证了所有连杆参数设计的合理性。

机器人眼球末端位移曲线如图2-19所示，表示机器人从初始位置运动到终止位置时，末端关节沿x，y，z方向的位移变化。

其位移变化三维图如图2-20所示。

其中各关节变量变化如图2-21所示。

机器人眼睑的运动学仿真，机器人眼睑的正运动学，建立如下坐标系，共设六个坐标系：S₁，S₂，S3，S4，S5，S6，如图2-22所示。机器人眼睑运动各杆件参数见表2-6。

表2-6 机器人眼睑运动各杆件参数表

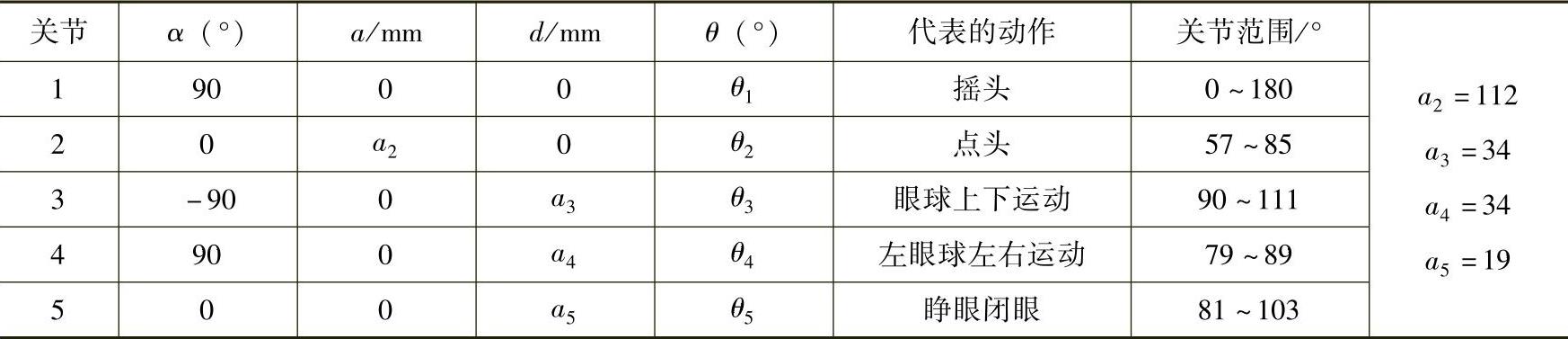
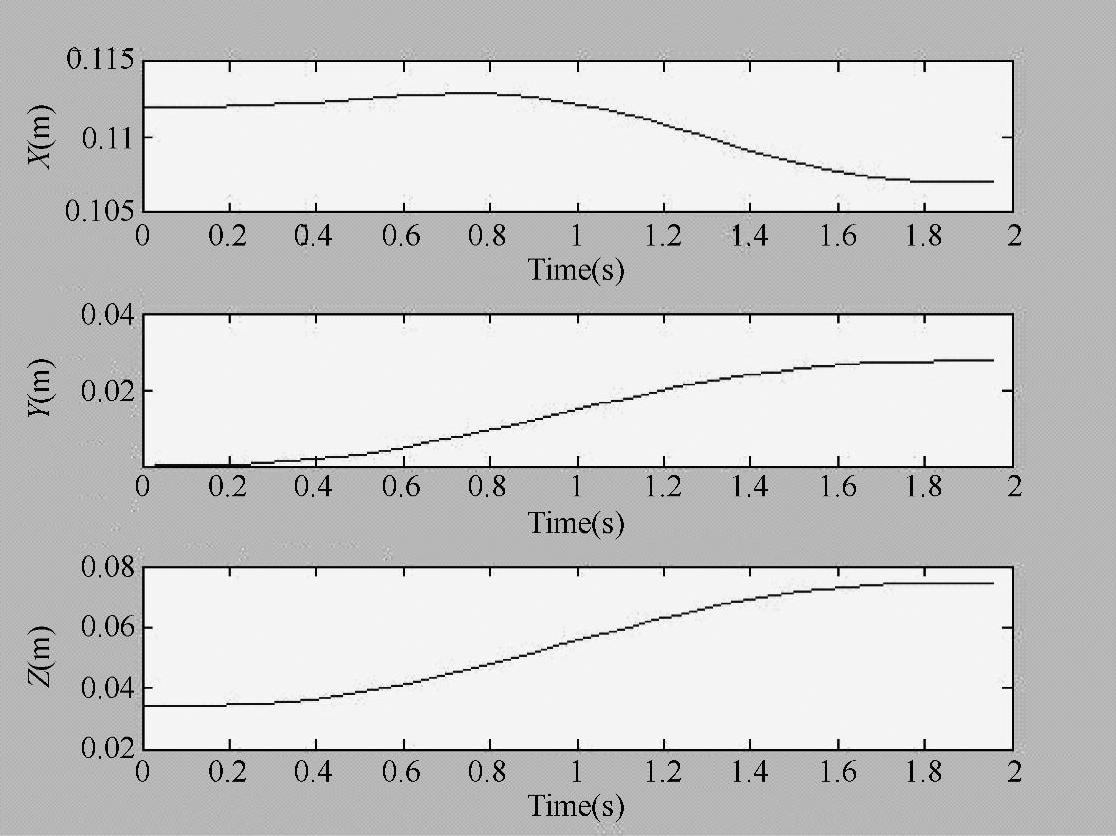
图2-19 机器人眼球末端位移曲线

图2-20 眼球位移变化三维图

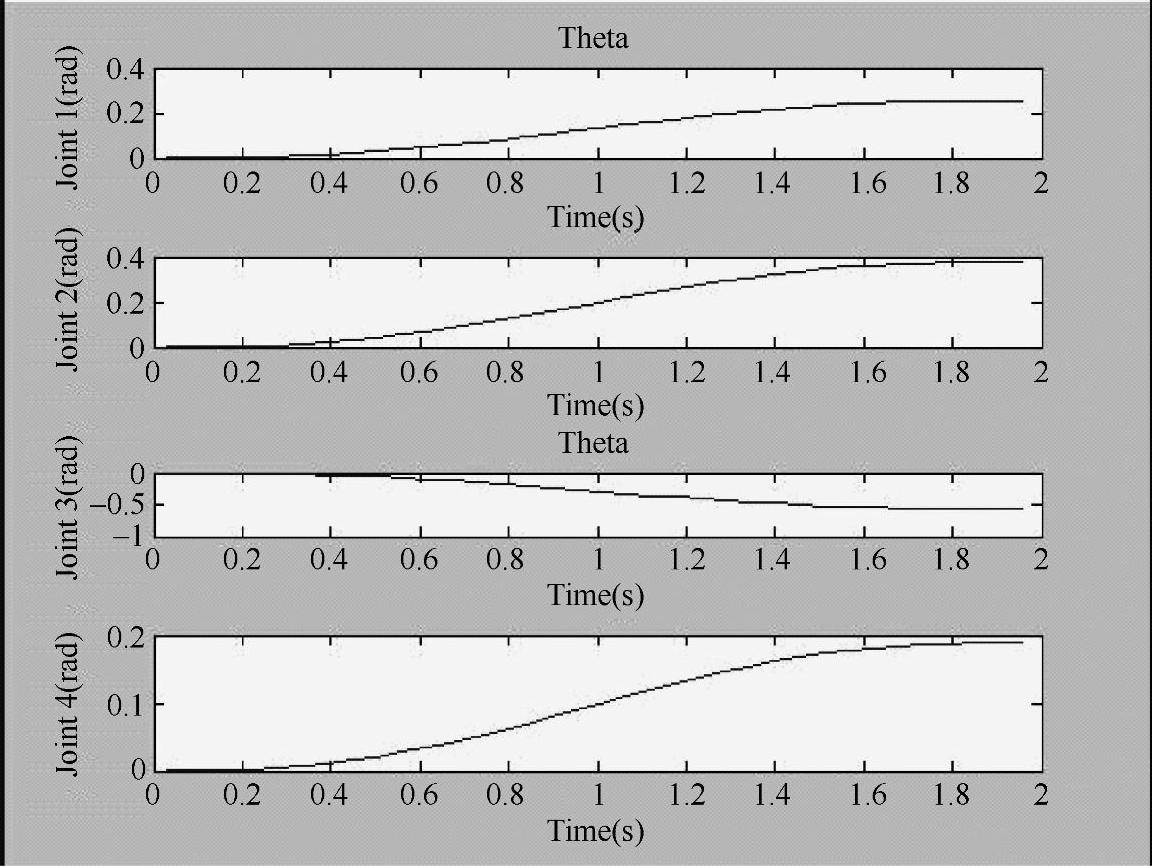
图2-21 各关节变量变化

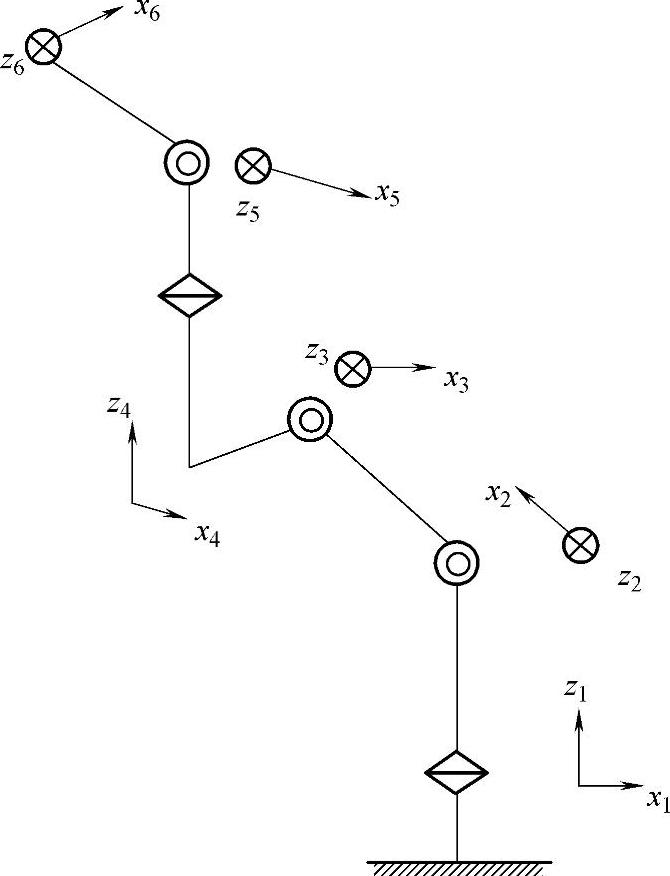
图2-22 机器人眼睑正运动学坐标系

两杆间的位姿矩阵，根据参数表和D-H公式可得

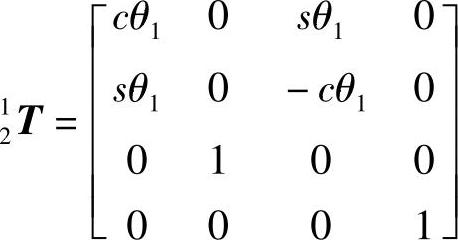
将各个连杆矩阵连乘得到₆¹T

式中

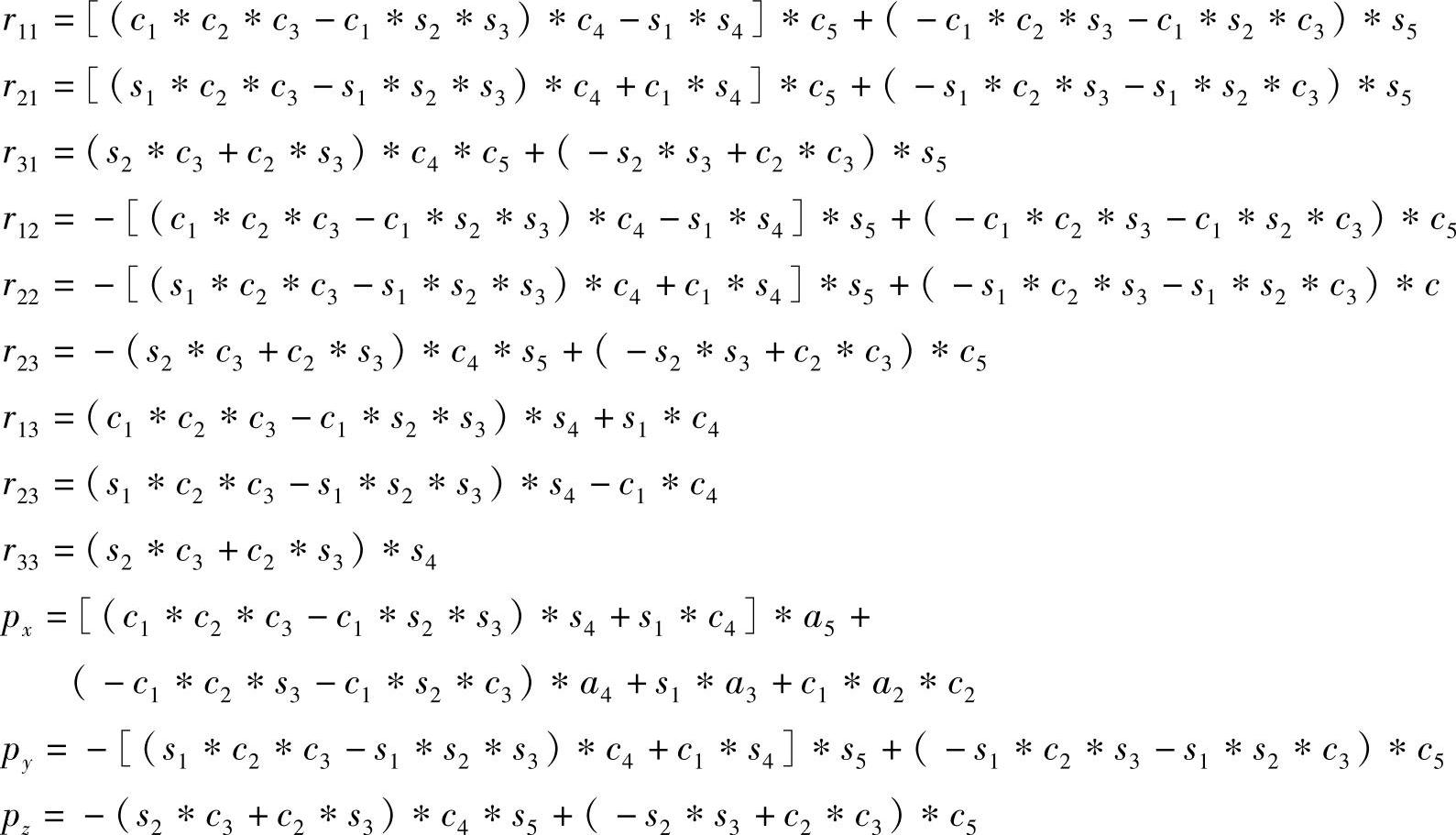
其中c_i=cosθ_i（i=1，2，3，4，5）；s_i=sinθ_i（i=1，2，3，4，5）

于是可得眼球作为末端执行器的姿态和位置分别是

机器人眼睑的运动仿真与眼球运动学仿真类似，可得如图2-23所示模型。

图2-23 机器人眼睑运动仿真图

其他仿真与以上两种仿真类似，至于其他运动部位都较眼球和眼帘运动简单，最多三个串联关节。