三棱锥上点的投影方案

【任务描述】

正三棱锥上点M的投影，如图 2-1所示。

图 2-1 三棱锥上M点的投影

【任务分析】

学习投影的基本知识，能够熟练地画出立体上各个点线的投影。

【知识准备】

正投影法以及点、线、面的投影知识。

当光线照射物体时，地面或墙面上会出现物体的影子，这就是我们说的投影现象。

当光线（我们称之为投影线）为平行光，把物体投影在墙面（我们称之为投影面）上，得到的影子（如图2-2），我们称之为投影。当投影线与投影面垂直时，我们称之为正投影。

1.正投影的基本性质

（1）显实性

当直线或平面与投影面平面平行时，则直线的投影反映实长；平面的投影反映实形，图2-2（a）。

（2）积聚性

当直线或平面与投影面平面垂直时，则直线的投影积聚成一点；平面的投影积聚成一条直线，图2-2（b）。

（3）类似性

当直线或平面与投影面平面倾斜时，其直线的长度变短；平面的投影面积变小，但投影的形状仍与原来的形状类似，图2-2（c）。

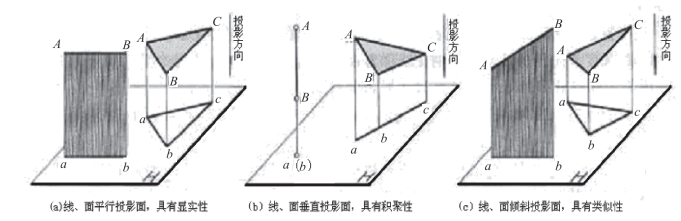
图2-2　正投影的特性

2.三视图

（1）视图的概念

用正投影法绘制的物体的投影，称为视图。

换句话说，就是把物体放在观察者和投影面之间，将观察者的视线视为一组相互平行且与投影面垂直的投射线，对物体进行投射所获得的正投影图，叫视图（如图2-3）。

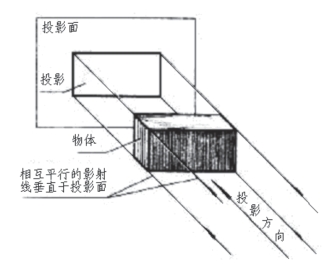
图2-3　视图的获得

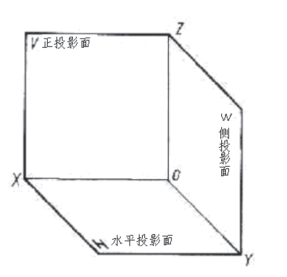
图2-4 三面投影体系

（2）三视图的形成

一般来说，一个视力是很难把一个物体的开关和大小表达清楚的，为此工程上常用三视图来表达物体的形状与大小。

首先，三面投影体系是将三个互相垂直的投影面所组成的（如图2-4）。它们分别为正投影面V面；水平投影面H面；侧投影面W面。

三个投影面的交线称为投影轴。投影轴的交点O称为原点。

将V面与H面的交线称为OX轴；将H面与W面的交线称为OY轴；将V面与W面的交线称为OZ轴。

其中X方向表现物体的长度方向，Y方向表现物体的宽方向，Z方向表现物体的高方向。

然后，将物体放置在三面投影体系中，按正投影法向各投影面投射，在不同的投影面上得到三个投影，我们称之为正面投影、水平投影、侧面投影，如图2-5（a）。

最后，为了画图方便将三个投影面展开在同一平面上。规定：V面不动，H面绕OX轴向下旋转90°，W面绕OZ轴向右旋转90°，如图2-5（b）。这样就得到了展开后的三视图，图2-5（c）。注意，旋转时，OY轴被分为两处，分别用OYH（在H面上）与OYW（在W面上）表示，如图2-5（d）。

V面的投影我们称为主视图；

H面的投影我们称为俯视图；

W面的投影我们称为右视图。

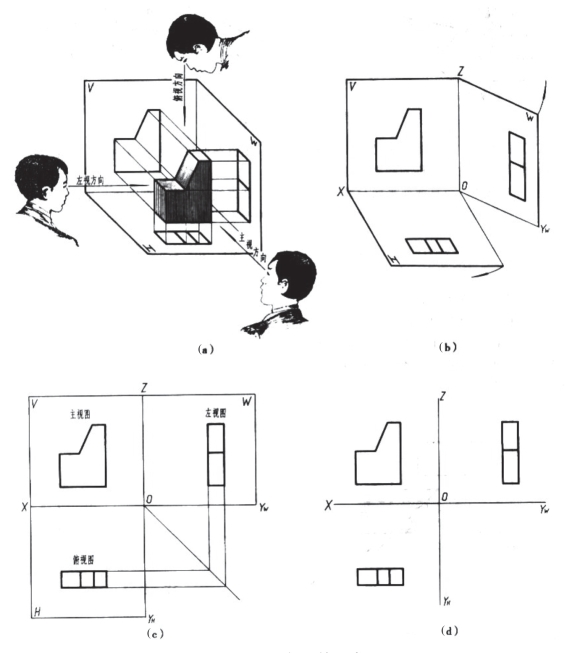
图2-5　三视图的形成

（3）三视图之间的关系

三视图的位置关系是：以主视图为准，俯视图在它的正下方，左视图在它的正右方。(https://www.xing528.com)

三视图的投影关系

由于主视图反映物体的长与高，俯视图反映物体的长与宽，右视图反映物体的高与宽，所以：

主、俯视图长对正（等长）；

主、右视图高平齐（等高）；

俯、右视图宽相等（等宽）。

3.点线投影的基本知识

空间形体都是由点、线、面等几何要求组成的，要识读或绘制空间形体的投影，点线面的投影，应该是基础。

（1）点的投影

点的投影仍是点。如图2-6所示，过空间点A分别向三投影面投影，得到三个投影点，分别为a、a′、a″，其中a是水平投影面的投影；a′是正投影面的投影；a″是侧投影面的投影。

投影图如图2-6（b），它也同样满足投影规律，即长对正，宽相等，高平齐。

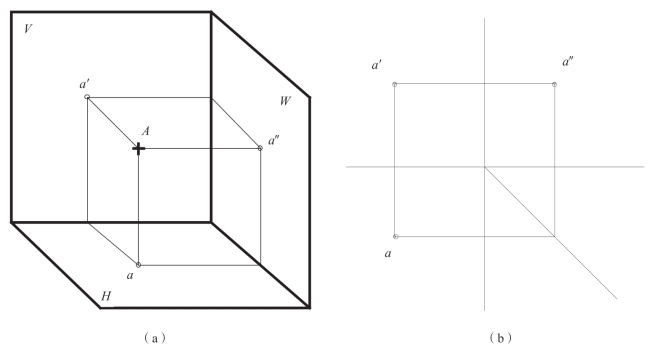
图2-6　空间点的A的投影

（2）直线的投影

直线的投影仍为直线，如图2-7所示。直线AB的水平投影ab、正面投影a′b′、侧面投影a″b″均为直线。

直线的投影可由直线上的两点的同面投影来确定，因空间一直线由直线上的两点来确定，所以直线的投影也可由直线上任意两点的投影来确定。

所以只要求得点A与点B的投影，然后分别连接，就可得到直线AB的三面投影。

（3）面的投影

平面的确定，可以是不在一条直线的三个点来决定；也可以是一直线与线外一点决定；也可由两相交直线来决定；或两平行直线来决定。

由于工程上的平面，多有有限面，所以，我们这里所讲的平面，是指平面图形。

图2-8所示的是三角形ABC所决定的平面的三面投影。

其实作图过程，就是先做出ABC三个点的投影，然后依次连接各点，即可得到三角形ABC的投影。

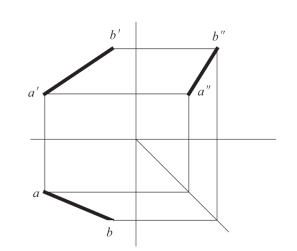
图2-7　直线的投影图

图2-8　平面的投影

【任务实施】

（1）连接s′m′并延长，与a′c′交于2′，如图2-9。

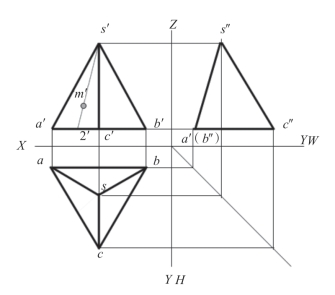
图2-9　步骤（1）

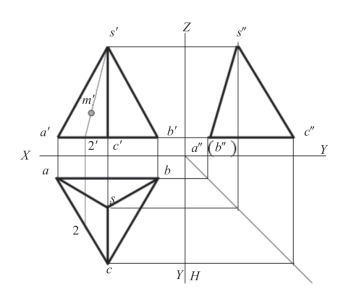
图2-10 步骤（2）

（2）在投影ac上求出Ⅱ点的水平投影2，如图2-10。

（3）连接s2，即求出直线sⅡ的水平投影，如图2-11。

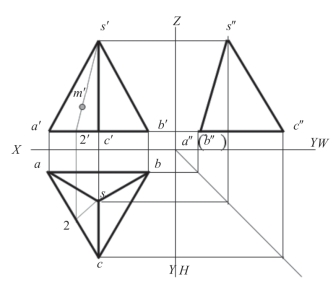
图2-11　步骤（3）

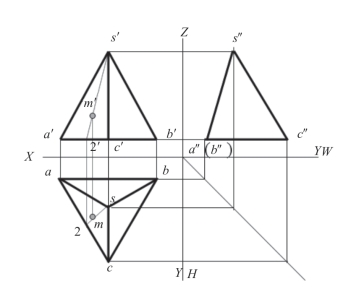
图2-12　步骤（4）

（4）根据在直线上的点的投影规律，求出M点的水平投影m，如图2-12。

（5）再根据点的三视图投影方法，求出m″，完成三视图，如图2-13。

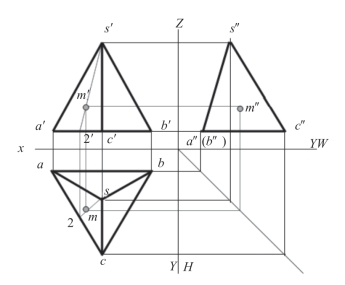
图2-13　步骤（5）