同步计数器的应用和优化策略

1）同步二进制加法计数器

图6.9给出的是一个同步4位二进制加法计数器，下面按时序电路的分析步骤对此电路进行分析。

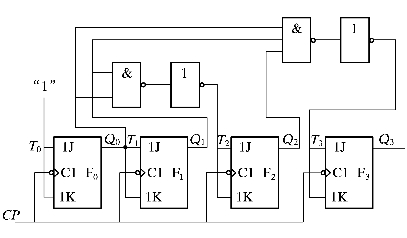
图6.9　同步二进制加法计数器逻辑图

（1）写方程

时钟方程：CP0=CP1=CP2=CP3=CP，同步时序电路。

（对于同步时序电路，因触发器同时满足有效的时钟条件，因此上面时钟方程也可省略不写）。

驱动方程：

输出方程：此电路除触发器端之外，没有另外的输出，故没有输出方程。

（2）求状态方程

T触发器的特性方程为

将驱动方程代入特性方程可得各触发器的状态方程：

（3）列状态表

由于此电路除了触发器的输入、输出端外，没有其余的输入、输出端，因而状态表中只需列出四个触发器的各种现态取值组合及相应的次态，如表6.5所示（设各触发器的初态Q3Q2Q1Q0=0000）。

表6.5　4位二进制加法计数器状态表

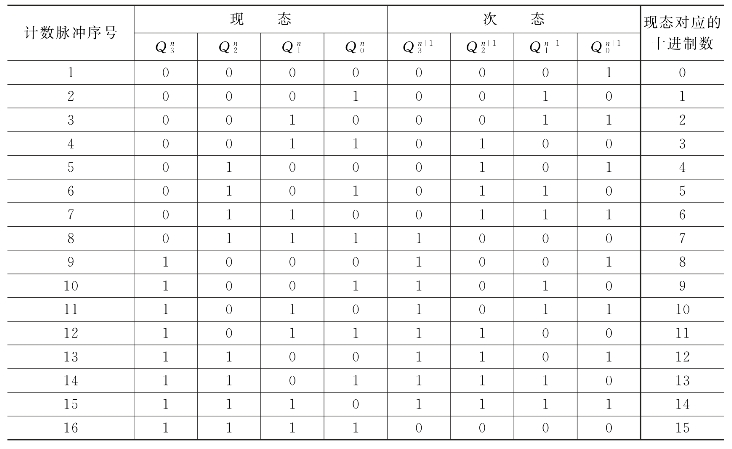
（4）画状态图和时序图

由表6.5可画出图6.10所示的状态图和时序图。

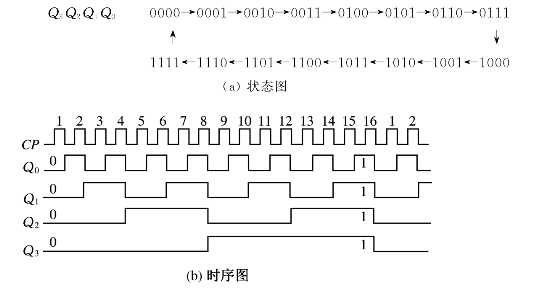
图6.10　同步4位二进制加法计数器

（5）检查能否自启动，说明功能

在图6.10（a）所示的状态图中只存在一个循环（有效循环），故能自启动，即电路无论落入哪种状态，在CP作用下，总是循环工作的。

由图6.10（a）所示的状态图可知，该电路是按二进制加法规律进行递增计数的，因此该电路的逻辑功能是能自启动的同步4位二进制加法计数器。

2）同步十进制加法计数器

该电路如图6.11所示。分析过程如下：

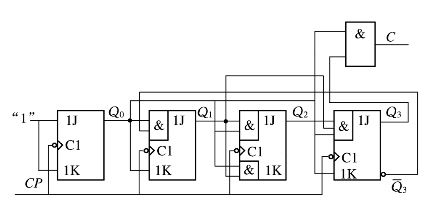
图6.11　同步十进制加法计数器逻辑图

（1）列方程

根据图6.11所示的逻辑电路图列出时钟方程、输出方程和驱动方程，其中：

时钟方程：CP0=CP1=CP2=CP3=CP，同步时序电路。

输出方程：

驱动方程：

（2）求状态方程

将上述驱动方程代入JK触发器的特性方程，可得四个触发器的状态方程：(https://www.xing528.com)

（3）列状态表

状态表见表6.6（设初始状态Q3Q2Q1Q0=0000）。

表6.6　同步十进制加法计数器状态表

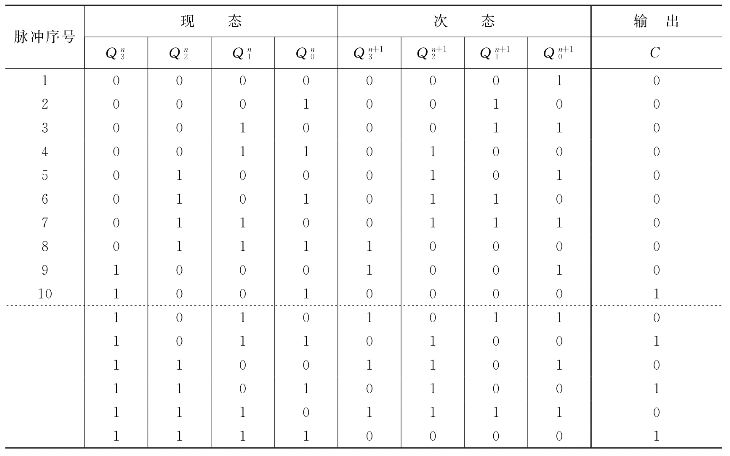
（4）画状态图和时序图

状态图及时序图见图6.12。

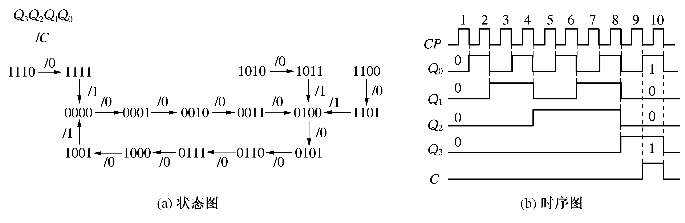
图6.12　同步十进制加法计数器

（5）检查能否自启动，说明功能

在图6.12（a）的状态图中仅存在一个有效循环，其他六个无效状态均可在时钟脉冲信号的作用下自动进入有效循环，故电路无论落入哪种状态，在CP作用下，总能自动进入有效循环，即能够自启动。

本逻辑电路为具有自启动功能的8421编码同步十进制加法计数器。

3）同步N进制计数器

试分析图6.13所示的时序电路的逻辑功能。

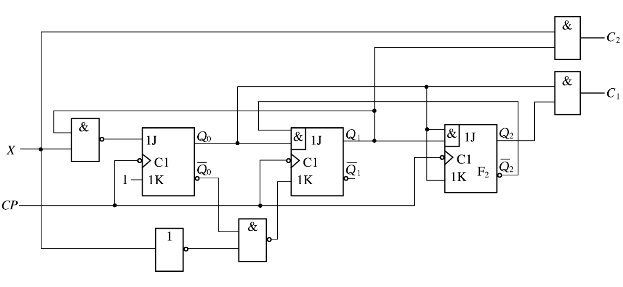
图6.13　时序电路逻辑图

分析结果如下：

（1）写方程

时钟方程：CP0=CP1=CP2=CP，同步时序电路。

驱动方程：

输出方程：

（2）求状态方程

将上述驱动方程代入JK触发器的特性方程求得状态方程：

（3）列状态表

此逻辑电路的状态表见表6.7。设初始状态Q2Q1Q0=000。

表6.7　图6.13所示同步时序电路状态表

（4）画状态图和时序图

状态图和时序图见图6.14。

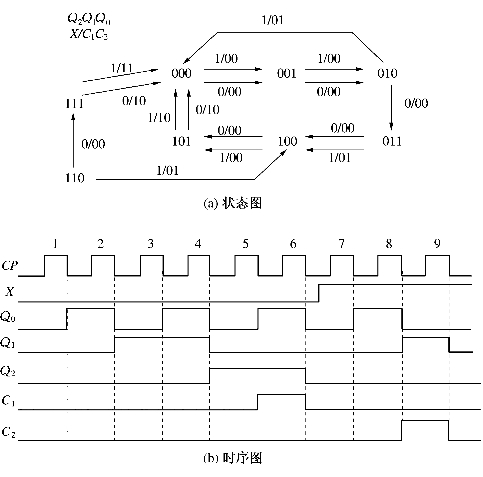
图6.14　同步N进制计数器

（5）检查自启动，说明功能

分析状态图可以看出，当输入信号X=0时，每加入6个时钟脉冲信号以后，电路的状态循环变化一次，由000～101六个有效状态构成有效循环；当输入信号X=1时，每加入3个时钟脉冲信号后，电路的状态循环变化一次，即由000～010三个有效状态构成有效循环。而无效状态（X=0时的110～111；X=1时的011～111）在CP脉冲作用下均能进入有效循环，说明该电路能够自启动。

通过分析可知，该逻辑电路是一个具有自启动功能的同步可控N进制加法计数器，控制信号X=0时为六进制加法计数器；控制信号X=1时为三进制加法计数器。