常用数制：十进制、二进制、八进制、十六进制对照表

数制是计数进位制的简称。在日常生活和生产中，人们习惯用十进制数；而数字系统，例如计算机，只能识别“0”和“1”构成的数码，所以经常采用的是二进制数和十六进制数，有些地方还用到八进制数。

1）十进制（Decimal）

十进制中有0～9十个数码，计数“基数”为10。数的组成是自左向右由高位到低位排列。计数时逢十进一，借一当十。数码在不同的位置代表的数值不同，称之为“位权”，简称为“权”。例如，十进制数616可以表示为：

其中102、101、100分别为百位、十位、个位的“权”，也即相应位的数码1所代表的实际数值。位数越高，权值越重，相邻位的权值关系是左边位的权是右边位权的10倍。任意一个十进制数，都可以表示为：

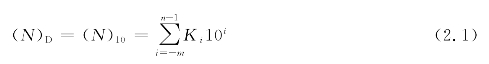
式中：Ki为十进制数第i位的数码；n表示整数部分的位数，m表示小数部分的位数，n、m都是正整数；10i为第i位的位权值，例如，十进制数54.214可表示为：

2）二进制（Binary）

二进制数由“0”和“1”两个数码组成，它的组成也遵循自左向右由高位到低位排列，每个数位的位权值为2的幂。计数时，逢二进一，借一当二，也就是说，二进制数的计数“基数”为2。任意一个二进制数，都可以表示为：

式中：Ki为二进制数第i位的数码；2i为第i位的位权值；n表示整数部分的位数，m表示小数部分的位数，n、m均为正整数，例如，二进制数1101.101可以展开为：(www.xing528.com)

3）十六进制（Hexadecimal）

十六进制数比二进制数位数少，便于书写和记忆，因此在计算机中经常使用。十六进制数有0～9和A、B、C、D、E、F共16个数码，它也是自左向右由高位向低位排列。其计数“基数”为16。计数时，逢十六进一，借一当十六。每个数位的位权值为16的幂。任意十六进制数可以表示为：

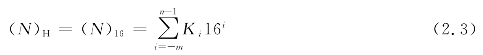
式中：Ki为十六进制数第i位的数码；16i为第i位的位权值；n、m的含义与式（2.1）和式（2.2）的含义相同，例如，十六进制数5A.B4可以表示为：

4）八进制（Octal）

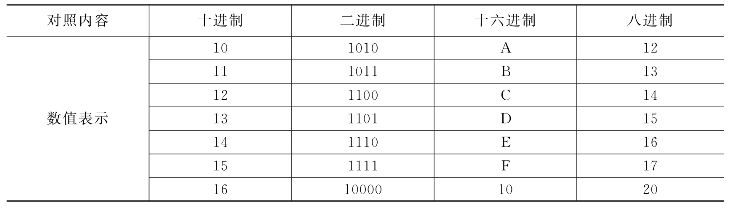
八进制数有0～7八个数码。其计数“基数”为8。计数时，逢八进一，借一当八。每个数位的位权值为8的幂。任意八进制数按位权展开的方法与二进制、十进制、十六进制数相同，在此不再赘述。表2.1为各种数制的对照表。

表2.1　数制对照表

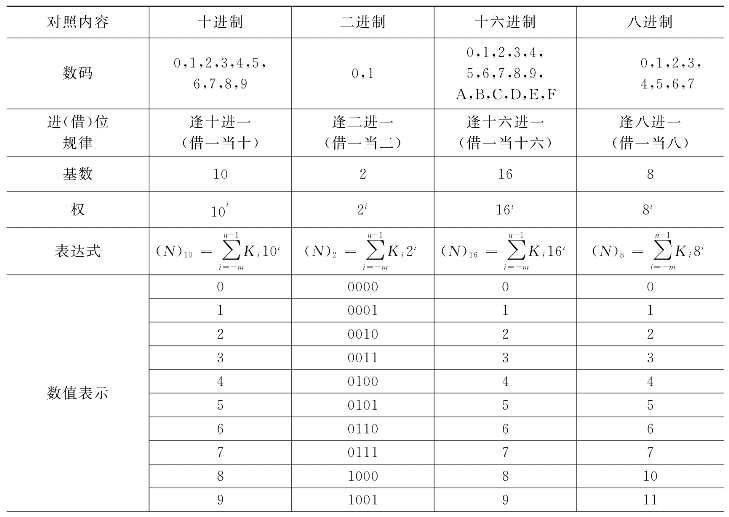
（续表2.1）