天然水流的扩散系数和离散系数研究

4.1.2.1　分子扩散系数Em

水中所含物质的分子扩散系数大小，主要与影响分子扩散运动的温度、溶质、压力有关，与水的流动特性无关，即分子扩散系数各向同性。水质计算中，分子扩散一般仅用于静止水体或流速很小时的情况。各物质在水中的分子扩散系数变化较小，约10-1～10-1m2／s，例如20℃下O2、NH3、酚的Em分别为1.8、1.76、0.84（10-1m2／s）。

4.1.2.2　紊动扩散系数Et

紊动扩散是紊动水流脉动流速引起的，紊动扩散系数的大小主要与水流的紊动特性有关，从而使垂向、横向和纵向的紊动扩散系数各异，即各向异性。

1.垂向紊动扩散系数Etz

对于一般的宽浅型河流，可根据雷诺比拟方法，即认为水流的质量交换与动量交换等同，紊动扩散系数等同于涡黏系数，依此推导得明渠垂向平均紊动扩散系数Etz为

式中：Etz为垂向平均紊动扩散系数；H为水深；u*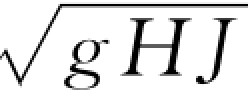＝，为摩阻流速；g为重力加速度；J为水力坡降。

对于水域广阔且比较深的湖泊、水库、海洋，温暖季节常常存在温度分层，即表面同温层、中间温跃层和下部同温层。这种情况下，根据实测资料分析，Etz的变化范围大体为：湖、海表面同温层Etz＝10～100（10-1m2／s），中间温跃层Etz＝0.01～1（10-1m2／s），下部同温层Etz＝0.1～10（10-1m2／s），底部边界层Etz＝1～10（10-1m2／s）；河口、海湾的Etz约1～10（10-1m2／s）。温跃层的Etz最小，表明对垂向紊动扩散具有抑制作用。

2.横向紊动扩散系数Ety

天然河流纵、横断面变化较大，岸边也会有各种建筑物，同时还可能有支流汇入、河道弯曲、叉道等情况，使垂向和横向的流速分布更不均匀，从而引起比较大的横向紊动扩散。目前一般仍采用垂向扩散系数的描述形式来表达横向紊动扩散系数，即

式中：α为经验性系数。对于顺直明渠，费希尔（Fischer）对70多个试验资料统计分析，发现除灌溉渠道α＝0.24～0.25外，几乎所有情况的α值都在0.10～0.20范围内；对于弯曲性河流，α值一般在0.4～0.8（河道收缩时取较小值，扩展时取较大值）；若弯曲很大，二次环流影响强烈，α可取1～3，应参考能反映河道弯曲影响的公式计算。

对于宽深比B／H≤100的河流，宜用泰勒公式计算

式中：B为河流平均宽度，m；其余符号意义同前。

3.纵向紊动扩散系数Etx

由于纵向离散系数Ed远比纵向紊动扩散系数大，一般可大出几十倍至上百倍，故常将纵向紊动扩散系数并入纵向离散系数中一起考虑。从有限的资料看，Etx与Ety可能处于同样的量级，约为Ety的3倍左右。

4.1.2.3　河流纵向离散系数Ed

河流纵向离散系数Ed，视资料条件的不同，可采用下述三种途径计算。

1.由断面流速分布资料推求

在天然河流中，河宽远远大于水深，横向流速不均匀对Ed的影响远大于垂向流速不均匀的影响。费希尔考虑这一实际，将天然河流简化为平面二维水流，如图4-3所示，然后按照埃尔德（J.W.Elder）由垂向流速分布推导纵向离散系数的方法，导得天然河道中纵向离散系数Ed（即Edx）的计算公式为

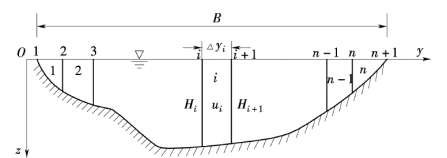
图4-3　河流断面分块示意图

参看图4-3，该式近似为(www.xing528.com)

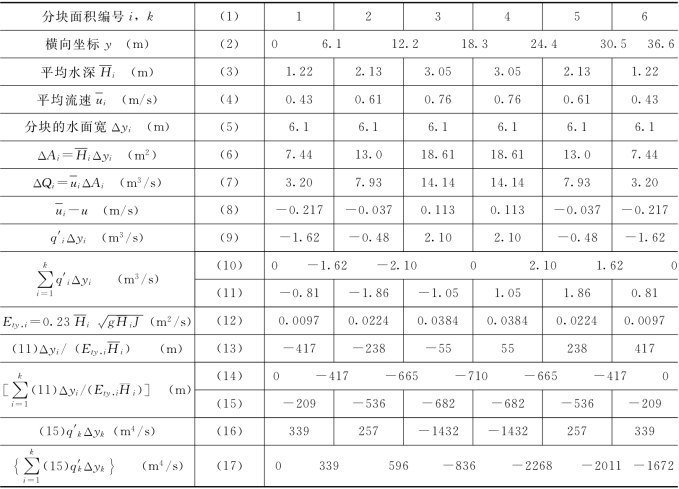
上式计算的是某一断面水流的Ed，对于较长河段应取若干个有代表性断面求得的Ed平均。下面举例说明如何应用断面流速分布资料计算Ed。

（4）按式（4-12a）计算纵向离散系数Ed：Ed＝-｛.｝／A＝-1672／78.1＝21.4m2／s。

表4-1　河流纵向离散系数Ed计算表

2.由现场示踪剂试验推求

为了比较准确地计算河段的纵向离散系数，可在河道中选择适当的位置瞬时以点源方式投放示踪剂，如诺丹明，在下游观测示踪剂浓度随时间变化的过程线来推求纵向离散系数Ed。示踪剂为非降解性物质，在上游某断面瞬间投入河流后，由于水流的迁移扩散作用，向下游流动过程中不断分散混合，因此在下游较远的断面上测得的是一条比较平缓的示踪剂浓度过程线。显然，该过程线的分布状况反过来也反映了河段的迁移扩散特征。尤其下游的监测断面均取在纵向混合区时，两监测断面过程线间的差异则比较好地反映了该河段污染物随水流迁移中的纵向离散特征。基于这一事实，该方法采用由下游不同断面观测的示踪剂浓度过程线推求Ed。当选取的下游断面均在纵向混合区时，浓度计算为一维水质问题，可由后面讲述的一维水质迁移转化基本方程解得下游x处的示踪剂浓度变化过程为

式中：x为以投放示踪剂的断面为起点至下游量测断面处的距离；t为以投放示踪剂的时刻为零点起算的时间；C（x，t）为x处t时刻的示踪剂浓度；M为瞬时面源强度，等于投放的示踪剂质量除以过水断面积；u为河段平均流速；Ed为纵向离散系数。

由式（4-13）可求得x处该过程线C（x，t）的方差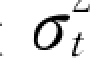为

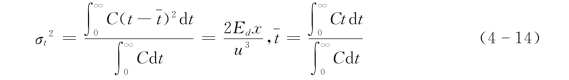
当用纵向混合河段距离分别为x1、x2的两个断面计算时，可得各断面浓度过程线的方差分别为

3.由经验公式估算

在缺乏断面流速分布资料和示踪剂试验时，可用经验公式估算。这类公式甚多，在许多关于水环境保护的文献中都有列举，但常常有一定的局限性，选用时需用当地资料检验，以保证成果的可靠性。对于一般性河流，以下公式可供实用中参考。

费希尔于1975年提出的公式为

刘享立（H.Liu）1980年提出的公式为

麦克奎维—凯弗（Mcquivey—keefer）1974年提出的公式为

爱尔德提出的公式为

Seo和Cheang（1966）由美国26条河流收集的59个实测资料，得到的公式为