预测污染负荷影响因素

影响点源污染负荷的主要因素有人口增长、工业产值、万元产值废水排放量、人均生活污水排放量、各种污染物浓度等，可根据具体情况采用适当的模型预测这些因素的未来变化，进而对污染负荷作出预测。

3.2.1.1　指数外延预测模型

如预测事件是一组随时间变化的数据，其变化发展趋势符合指数增长规律，可由以往的资料建立指数曲线方程，依此来推测未来事件发展趋势与状态。指数增长模型的一般形式为

式中：P0为基准年（t＝0）的变量值，基准年一般可根据国民经济发展计划情况确定；t为从基准年开始至预测年份的时间；P为预测的第t年的变量值；α为预测期内预测变量的平均增长率。

α不是一个固定不变的常数，而是一个随时间有一定变化的数值。譬如说α指发展增长率，例如某地在预测国民经济1990～2100年间的变化时，按当地计划部门提供的情况，前10年的平均增长率为6%～7%，后10年为8%～9%。又如用于人口预测，则平均年增长率可根据国家及地区计划的人口增长率来确定。

3.2.1.2　皮尔生长曲线预测模型

生长曲线预测模型种类颇多，其中皮尔模型比较常用，现以万元产值工业废水排放量预测为例介绍如下：万元产值工业废水排放量是一个比较宏观的特征参数，它代表一个地区整个工业，或其中某一行业平均生产万元价值产品产生的工业废水量，而不表示个别企业的废水生产率的大小；且已经包括生产工艺的改进，各种节水措施等科学技术进步、生产管理水平提高等因素的作用，因而万元产值工业废水量是逐年减少的（负增长），一直减少到某一极限值，但不可能减少到零。

皮尔生长曲线方程描述的是正增长曲线，当预测变量P（如万元产值工业废水量）为衰减变化时，则需通过下式转换为增长变化

式中：P为正增长的皮尔生长曲线变量值；p为衰减变化（负增长）的曲线变量值；2A为p的上限值，由实际资料估计。

皮尔生长曲线方程为

式中：a、b、K为三个参数。

已知时间序列（Pi，ti），上式可写成

应用最小二乘法原理，可由实际系列（Zi，Pi）求得参数α、β，再求得a和K

由此可导出参数b的公式为

【例3-1】 有9组时间系列资料（ti，pi）列于表3-2中第（2）栏、第（3）栏，试依此推求皮尔生长曲线方程，并预测1990年的预测变量值。

表3-2　2A＝600时Pi、Zi计算表

解：

（1）原系列为减变量变化pi，需按式（3-2）转换为增变量变化Pi，列于第（4）栏，并由pi系列估计得2A＝600；

（2）由式（3-4c）计算Zi，列于第（5）栏；

（3）按最小二乘法由Pi、Zi计算得(www.xing528.com)

（4）按式（3-6）计算得：a＝0.8512，K＝240；

（5）由式（3-7）计算得：b＝6.36；

（6）将A、a、b、K代入式（3-3）和式（3-2），即得减变量情况下的皮尔生长曲线预测模型：

据此预测1990年（ti＝14）的预测变量值为360。

3.2.1.3　龚柏兹预测模型

龚柏兹曲线也是一种常用的生长曲线，它的数学模型的一般形式为

式中：P为预测变量；t为时间；k、a、b为参数。

对不同的参数值，龚柏兹曲线有不同的形状和变化趋势，既可以是增长曲线，也可以是下降曲线。k为曲线的上限或下限值。

已知时间系列值（ti，Pi），应用龚柏兹曲线拟合，即可求得参数k、a、b。现介绍一种较简单的求解方法，具体步骤如下。

（1）时间系列值的个数N应能被3整除，即等分为3组，每组n（n＝N／3）项。

（2）将各组变量值P1i、P2i、P3i取对数，并求得三组数据值的和：∑lgP1i，∑lgP2i，∑lgP3i。

（3）利用下列公式计算参数k、a、b

将求得的k、a、b代入式（3-9），即得该模型的预测方程。

【例3-2】 表3-3为某地用水总量时间系列数据（ti，Pi），试用龚柏兹曲线模型预测2000年该地区的用水总量。

表3-3　某地用水总量时间系列数据（ti，Pi）及预测

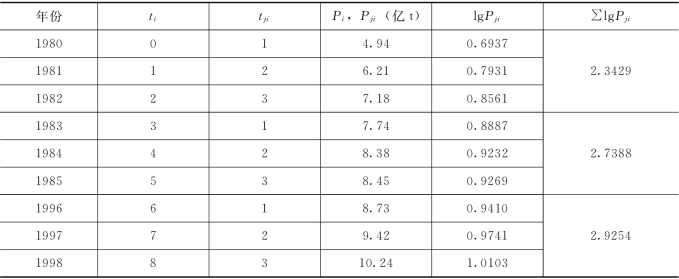
解：

（2）将b，a，k代入式（3-9），得预测模型

（3）预测2000年的用水总量