1.洁净滤袋的阻力损失△p0
阻力损失的大小与过滤速度vF和气体粘性系数μ成正比,迄今仍使用下面两个沿用已久的公式:
威廉姆斯式 △p0=K0vF (5-93)
穆姆福德式 △p0=ζμvF (5-94)
式中 △p0——清洁滤袋的压力损失(Pa);
K0——清洁滤袋的系数;
vF——过滤速度(m/min);
ζ——阻力系数;
μ——气体粘性系数(Pa·s)。
当滤材为织制滤布时,有人提出以下公式:

式中 CD——滤布阻力系数;
εf——滤布孔隙率(%);
其他符号同前。
其中,阻力系数CD由下面的经验公式求得:

式中 Re——雷诺数;
Df——滤布纤维的直径(m);
R——滤布孔隙,水力半径(m);
其他符号同前。
另外,当Df/R>10时,公式(5-96)可简化为公式(5-97),实际应用的织布几乎都处于这一尺寸范围内。

从式(5-94)、式(5-95)和式(5-97)可导出:

2.滤布粘有粉尘时的阻力△p
设△pd为粉尘层本身造成的阻力,则滤布粘有粉尘的阻力△p可用下面的公式来表示:
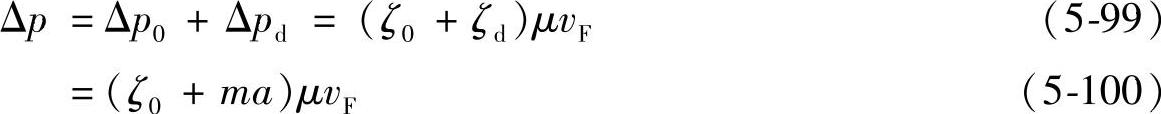
式中 m——总的荷尘量;
a——整个粉尘层的平均阻力系数。
在实用范围内不应把a看成恒定值,它与粉尘性质有关。
另外,有人提出过下面的两个简化公式:
△p=(a+bmq)vF (5-101)
△p=(A+BMδ)vF (5-102)
式中 a、b——系数;
A、B——系数;
q——指数;
δ——指数;
M——二次荷尘量(kg/m2)。
公式(5-101)是公式(5-100)的改写形式,而公式(5-102)把清灰粉尘时残留的粉尘层和滤材加以合计,在系数A中一起考虑;M是粉尘振落后,重新堆积起来的粉尘层的荷尘量。这样就便于对清灰过程进行分析,因为q在1的上下有很大的变化,而δ可以近似地取为1,因此就方便多了。
另外也有把上面的A设为BW,W为假想的残留荷尘量,这时设δ=0.1,即可得公式(5-103):(https://www.xing528.com)
△p=B(W+M)vF (5-103)
上述几个公式的系数值,若不经现场实测就无法掌握和运用,在长期使用过程中其值还有变化。所以这些公式实用价值不大。解决这个问题的途径之一是根据现场实测的阻力损失数据来找出估算这些系数的解析方法。此外,还要把粉尘堆积层作为粉尘充填层,应用柯捷尼-卡曼公式来进行理论计算的尝试。但后者不是最致密的充填层,卡曼常数不能取5,所以,即使已知粉尘的比表面积和充填率,仅通过计算还是求不出阻力损失。反之,如果取卡曼常数为5,用实测阻力损失和比表面积反算粉尘的充填率,则通过图5-39归纳大量的实测值之后,即可用该图由下式估算出粉尘层阻力系数和阻力损失。
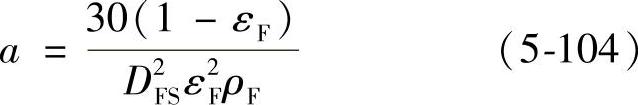
把该式代入式(5-100)即求出阻力损失。

图5-39 滤布上粉尘层的视在孔隙率
3.计算例1
已知粉尘的比表面积粒径DFS=0.5μm,尘粒密度ρF=3g/cm3,过滤速度vF=1m/min,用短纤维滤布,试求当捕集的粉尘量达m=0.2kg/m2时,粉尘层的阻力损失。
解:由图5-39可知,DFS=0.5μm时的粉尘层孔隙率为εF=0.95。根据公式(5-104),阻力系数a为:
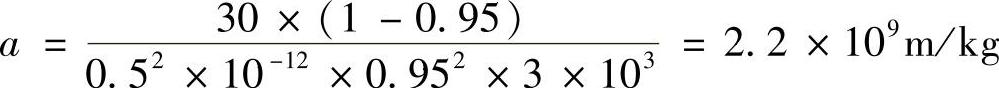
将其公式代入式(5-100),则:

下面的两个公式是归纳了实验结果后得到的

式中 ci——袋式滤尘器进口粉尘浓度(g/m3);
vF——过滤速度(m/min);
t——过滤时间(min);
DF——粉尘粒径(μm)。
系数K列于表5-10中。
4.计算例2
已知粉尘粒径DFS=10μm,过滤速度vF=1.0m/min,入口处的粉尘浓度Ci=5g/m3,试求用透气性为15cm/s的起毛滤布过滤30min时的阻力。
解:根据公式(5-106),并使用表5-10求出K,代入公式(5-105)后可得:

表5-10 系数K的各种参数值

5.滤料和粉尘层的阻力损失值
①滤料阻力损失:滤料的阻力特性以洁净滤料阻力系数和残余阻力表示,其值见表5-11。
表5-11 滤料阻力特性

注:摘自GB/T6719—2009。
②粉尘层阻力:粉尘层阻力按粉尘性质不同差异较大,表5-12给出一般情况下不同滤尘量和过滤速度时滤袋阻力值。
表5-12 不同滤尘量的滤袋过滤阻力

注:摘自张殿印、张学义编著《除尘技术手册》。
6.诱导器阻力
文氏管诱导器的阻力由图5-40查得。

图5-40 文氏管诱导器阻力
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




